ホームページ >バックエンド開発 >PHPチュートリアル >2 つのポイント グループを接続するための最小コスト
2 つのポイント グループを接続するための最小コスト
- 王林オリジナル
- 2024-09-01 06:34:061179ブラウズ
1595年。 2 つのポイント グループを接続するための最小コスト
難易度: 難しい
トピック: 配列、動的プログラミング、ビット操作、行列、ビットマスク
点の 2 つのグループが与えられます。最初のグループのサイズは 1 ポイント、2 番目のグループのサイズは 2 ポイント、サイズ 1 > です。 = サイズ2.
任意の 2 点間の接続のコストは、size1 x size2 行列で与えられます。ここで、cost[i][j] は点 i を接続するコストです。最初のグループと 2 番目のグループの点 j。 両方のグループの各点が反対側のグループの 1 つ以上の点に接続されている場合、グループは接続されています。つまり、最初のグループの各点は 2 番目のグループの少なくとも 1 つの点に接続され、2 番目のグループの各点は最初のグループの少なくとも 1 つの点に接続されている必要があります。
2 つのグループを接続するために必要な最小コストを返します。
例 1:
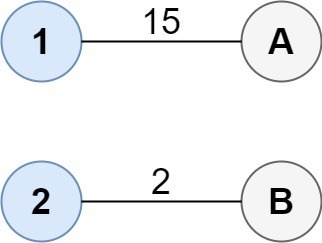
- 入力: コスト = [[15, 96], [36, 2]]
- 出力: 17
- 説明: グループを接続する最適な方法は次のとおりです。
1--A 2--B This results in a total cost of 17.
例 2:
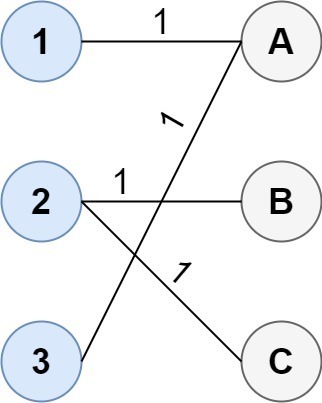
- 入力: コスト = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
- 出力: 4
- 説明: グループを接続する最適な方法は次のとおりです。
1--A 2--B 2--C 3--A This results in a total cost of 4.
最初のグループのポイント 2 と 2 番目のグループのポイント A に複数のポイントが接続されていることに注意してください。接続できる点数に制限はないので問題ありません。私たちは最小の総コストのみを考慮します。
例 3:
- 入力: コスト = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
- 出力: 10
制約:
- サイズ1 == コスト.長さ
- サイズ2 == コスト[i].length
- 1 1、サイズ2
- サイズ1 >= サイズ2
- 0
ヒント:
- 左側の各ポイントは、左側のノードに既に接続されているポイントに正確に接続されるか、どのノードにも接続されていない右側のノードのサブセットに接続されます。
- ビットマスクを使用した動的プログラミングを使用します。状態は (最初のグループに割り当てられたポイントの数、2 番目のグループに割り当てられたポイントのビットマスク) になります。
解決策:
ビットマスクを使用した動的プログラミングを活用できます。このアイデアは、最初のグループの各ポイントを考慮し、それを 2 番目のグループのすべてのポイントに接続することでコストを最小限に抑えることです。
ビットマスキングを使用したダイナミック プログラミング (DP) アプローチ
手順:
-
状態の表現:
- DP テーブル dp[i][mask] を使用します。ここで:
- i は最初のグループのインデックスです (0 から size1-1 までの範囲)。
- マスクは、2 番目のグループ内のどの点が接続されているかを表すビットマスクです。
- DP テーブル dp[i][mask] を使用します。ここで:
-
状態遷移:
- 最初のグループの各ポイントについて、2 番目のグループのすべてのポイントに接続して、それに応じて DP テーブルを更新します。
- 2 番目のグループの新しいポイントが接続されている場合は、マスク内の対応するビットを更新します。
-
基本ケース:
- dp[0][0] = 0 (最初は接続なし) から開始します。
-
目標:
- dp[size1][(1
このソリューションを PHP で実装してみましょう: 1595。 2 つのポイント グループを接続するための最小コスト
<?php
/**
* @param Integer[][] $cost
* @return Integer
*/
function connectTwoGroups($cost) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$cost1 = [[15, 96], [36, 2]];
$cost2 = [[1, 3, 5], [4, 1, 1], [1, 5, 3]];
$cost3 = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]];
echo connectTwoGroups($cost1) . "\n"; // Output: 17
echo connectTwoGroups($cost2) . "\n"; // Output: 4
echo connectTwoGroups($cost3) . "\n"; // Output: 10
?>
説明:
- DP 配列 dp[i][mask] には、グループ 1 の最初の i 点をマスクで示されるグループ 2 の点と接続するための最小コストが格納されます。
- ネストされたループは、i とマスクの各組み合わせを反復し、すべての可能な接続を考慮して最適なコストを見つけようとします。
- 最終的に、ソリューションは 2 番目のグループの一部のポイントがまだ接続されていない可能性があるシナリオを考慮して最小コストを計算し、すべてのポイントが接続されていることを確認します。
このアプローチは問題の制約を効率的に処理し、2 つのグループを接続するためのコストを最小限に抑えます。
連絡先リンク
このシリーズが役立つと思われた場合は、GitHub で リポジトリ にスターを付けるか、お気に入りのソーシャル ネットワークで投稿を共有することを検討してください。あなたのサポートは私にとって大きな意味を持ちます!
このような役立つコンテンツがさらに必要な場合は、お気軽にフォローしてください:
- GitHub
以上が2 つのポイント グループを接続するための最小コストの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

