数十年ぶりに進歩が見られ、見習いのタオ・ゼシュアンさんとチャオ・ユーフェイさんが組み合わせ数学の問題を突破した

最近、数十年来の未解決の数学的問題に初めて進歩が見られました。

この進歩を推進しているのは、UCLA 大学院生の James Leng 氏と MIT 数学大学院生の Ashwin Sah 氏、およびコロンビア大学助教授 Mehtaab Sawhney 氏です。その中で、ジェームズ・レンは有名な数学者のテレンス・タオに師事し、アシュウィン・サーは離散数学の達人である趙玉飛に師事しました。

論文アドレス: https://arxiv.org/pdf/2402.17995

この研究で達成された画期的な成果を理解するには、等差数列から始める必要があります。

等差数列の最初の n 項の合計は等差級数と呼ばれ、等差級数とも呼ばれます。 1936 年、数学者のパウル・エルデシュとパル・トゥランは、集合が整数のゼロ以外の部分 (0.00000001% であっても) で構成されている場合、その集合には任意の長さの等差級数が含まれているに違いないと推測しました。等差級数を回避できる唯一のセットは、整数の「無視できる」部分を含むセットです。たとえば、各数値が前の数値の 2 倍である集合 {2、4、8、16、…} は、進行することなく数値軸に沿って広がります。

1975 年、数学者のエンドレ・セメレディがこの予想を証明しました。彼の研究は、数学者が今日でも模索しているさまざまな研究の方向性を生み出しました。

数学者は、有限の数値セット (1 からある数値 N までのすべての整数) の場合におけるセメレディの結果を確立しました。禁止されたシリーズを必然的に含める前に、セットで初期プールのどれだけを使用できますか? N が変化すると、この割合はどのように変化しますか?

たとえば、N を 20 とします。長さが 5 つ以上の数字の系列を避けながら、これら 20 の数字のうちいくつ書き出すことができますか?答えは、初期プールの 16% ～ 80% であることが判明しました。

Szemerédi は、N が増加するにつれて、この分数はゼロに縮小する必要があることを最初に示し、それ以来、数学者はこれがどのくらいの速さで起こるかを定量化しようとしました。

昨年、2 人のコンピューター科学者による画期的な研究により、{6, 11, 16} などの 3 項系列の問題がほぼ解決されました。しかし、4 項以上の等差級数を避けようとすると、問題はさらに難しくなります。これは、長い系列が古典的な数学的手法を使用して明らかにするのが難しい基礎的な構造を反映しているためです。

3 項の等差級数の数値 x、y、z は常に、単純な方程式 x – 2y + z = 0 を満たします (級数 {10, 20, 30} を例にとります: 10 – 2*(20) + 30 = 0)、セットにこの条件を満たす数値が含まれているかどうかを証明するのは比較的簡単です。 4 項の級数の数値は、より複雑な方程式 x^2 – 3y^2 + 3z^2 – w^2 = 0 も満たさなければなりませんが、5 項以上の級数の場合はさらに複雑な方程式を満たす必要があります。これは、そのようなシリーズを含むセットがより微妙なパターンを示すことを意味します。数学者にとって、そのようなパターンが存在するかどうかを証明することも困難になるでしょう。

1990 年代後半、数学者のティモシー ガワーズは、この障害を克服する理論を提案しました。彼は後にこの業績の功績もあり、数学界最高の栄誉であるフィールズ賞を受賞した。 2001 年に、彼は自分の方法をセメレディの定理に適用し、最大セット サイズのより適切な制限を証明し、特定の長さに対する等差級数を回避しました。

2022 年、当時 UCLA 大学院 2 年生だったジェームス レンは、ガワーズの理論を理解し始めました。彼はセメレディの定理を考慮しませんでした。その代わりに、彼はガワーズのアプローチに関する質問に答えたいと考えている。

しかし、1年以上懸命に探索しましたが、何も見つかりませんでした。

関連する問題について考えてきたサーとソーニーは、レンの研究について知り、非常に興味を持ち、「私がこのように考えることができることに驚いています。」とさえ言いました。

サーとソーニーは、レンの研究がシェメレディの定理のさらなる進歩に役立つ可能性があることに気づきました。数か月以内に、3 人の若い数学者が、五項級数を使用せずに集合のサイズの上限をより適切に求める方法を考え出しました。その後、彼らは研究を一連の任意の長さに拡張し、ガワーズの証明以来 23 年間で初めてこの問題に関する進歩を記録しました。

k項を持たない等差級数の最大部分集合のサイズを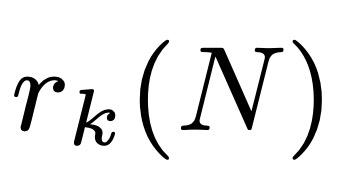で表すことにします。 Leng、Sah、Sawhney は、k ≥ 5 の場合、 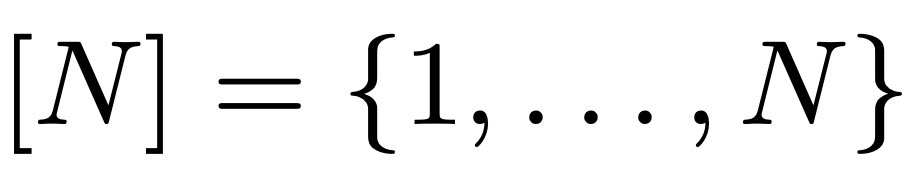となる c_k > 0 が存在することを示しました。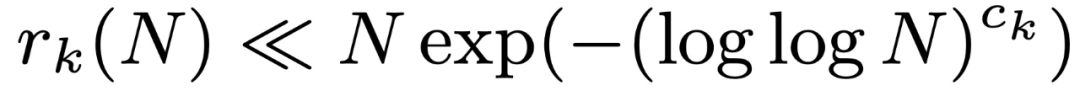

研究チーム

この論文の筆頭著者である James Leng は、カリフォルニア大学ロサンゼルス校 (UCLA) の数学の大学院生であり、カリフォルニア大学バークレー校で学士号を取得しています。彼は有名な数学者テレンス・タオに師事しました。

James Leng の研究対象には、算術組み合わせ論、力学システム、フーリエ解析などが含まれます。彼の研究は NSF 大学院生フェローシップによっても支援されています。

^{2016 年の夏、16 歳のサーは国際数学オリンピック (IMO) で金メダルを獲得し、翌年 MIT に入学しました。}

アシュウィン・サー

^{MIT での在学中、サーの数学的発展に重要な役割を果たした 2 人の人物がいます。一人目は、離散数学の修士であり、サーの大学院家庭教師でもあるユーフェイ・チャオ教授です。} 2人目はメーターブ・ソーニーです。彼らはクラスで出会って友達になりました。その後、二人は一緒に研究を行い、グラフ理論、確率理論、ランダム行列の性質など、離散数学の分野におけるさまざまなトピックについて議論しました。 Ashwin Sah と Mehtaab Sawhney は、(MIT) の学部生だった 2017 年末に知り合いました。それ以来、二人は 57 もの信じられないほどの数学的証明を共同で書き上げ、その多くはさまざまな分野に重大な影響を与えてきました。

Mehtaab Sawhney

^{Mehtaab Sawhney は現在、コロンビア大学の助教授です。彼の研究対象には、特に組み合わせ論、確率、理論的なコンピューターサイエンスが含まれます。}

参考リンク：https://www.quantamagazine.org/grad-students-find-inevitable-patterns-in-big-sets-of-numbers-20240805/

以上が数十年ぶりに進歩が見られ、見習いのタオ・ゼシュアンさんとチャオ・ユーフェイさんが組み合わせ数学の問題を突破したの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。