ホームページ >バックエンド開発 >Python チュートリアル >最大部分配列問題と kadane アルゴリズム
最大部分配列問題と kadane アルゴリズム
- 王林オリジナル
- 2024-08-14 11:08:011207ブラウズ
最大部分配列問題とその歴史
1970 年代後半、スウェーデンの数学者ウルフ グレナンダーは、画像データの 2D 配列を総当たり法よりも効率的に分析するにはどうすればよいかという問題について議論していました。当時のコンピューターは遅く、画像は RAM に比べて大きくなっていました。さらに状況を悪化させるのは、最悪の場合、ブルート フォースには O(n^6) 時間 (六次時間計算量) がかかりました。
まず、Grenandier は質問を単純化しました。数値の 1 次元配列が与えられた場合、最大の和を持つ連続した部分配列を最も効率的に見つけるにはどうすればよいでしょうか?
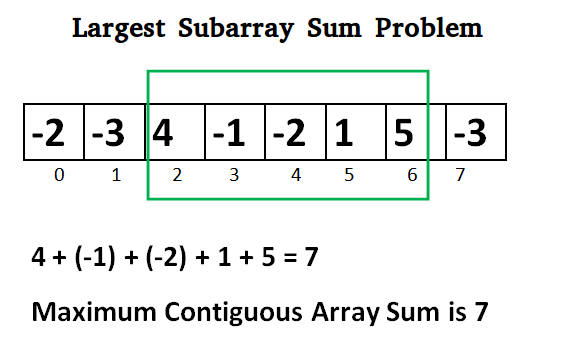
ブルート フォース: 3 次時間計算量を使用した素朴なアプローチ
力ずくで、1D 配列を解析する時間は 2D 配列の半分であるため、考えられるすべての組み合わせ (3 次時間計算量) を調べるには O(n^3) かかります。
def max_subarray_brute_force(arr):
max_sum = arr[0] # assumes arr has a length
# iterate over all possible subarrays
for i in range(len(arr)):
for j in range(i, len(arr)):
current_sum = 0
# sum the elements of the subarray arr[i:j+1]
for k in range(i, j + 1):
current_sum += arr[k]
# update max_sum if the current sum is greater
max_sum = max(max_sum, current_sum)
return max_sum
print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")
Grenander の O(n²) 最適化: 一歩前進
Grenander はそれを O(n^2) ソリューションに改良しました。私の調査では彼のコードは見つかりませんでしたが、私の推測では、彼は単に 2 つのインデックス間の数値をすべて合計する最も内側のループを削除しただけだと思われます。代わりに、部分配列を反復処理しながら累計を維持できるため、ループの数が 3 つから 2 つに減ります。
def max_subarray_optimized(arr):
max_sum = arr[0] # assumes arr has a length
# iterate over all possible starting points of the subarray
for i in range(len(arr)):
current_sum = 0
# sum the elements of the subarray starting from arr[i]
for j in range(i, len(arr)):
current_sum += arr[j]
# update max_sum if the current sum is greater
max_sum = max(max_sum, current_sum)
return max_sum
シャモスの分割統治: O(n log n) で問題を分割する
グレナンダーはコンピューター科学者のマイケル・シャモスに問題を見せました。シャモスは一晩考えて、O(n log n) という分割統治法を思いつきました。
なかなか賢いですね。このアイデアは、配列を 2 つの半分に分割し、各半分の部分配列の最大合計と、中点を横切る部分配列を再帰的に見つけることです。
def max_crossing_sum(arr, left, mid, right):
# left of mid
left_sum = float('-inf')
current_sum = 0
for i in range(mid, left - 1, -1):
current_sum += arr[i]
left_sum = max(left_sum, current_sum)
# right of mid
right_sum = float('inf')
current_sum = 0
for i in range(mid + 1, right + 1):
current_sum += arr[i]
right_sum = max(right_sum, current_sum)
# sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
return left_sum + right_sum
def max_subarray_divide_and_conquer(arr, left, right):
# base case: only one element
if left == right:
return arr[left]
# find the midpoint
mid = (left + right) // 2
# recursively find the maximum subarray sum for the left and right halves
left_sum = max_subarray_divide_and_conquer(arr, left, mid)
right_sum = max_subarray_divide_and_conquer(arr, mid + 1, right)
cross_sum = max_crossing_sum(arr, left, mid, right)
# return the maximum of the three possible cases
return max(left_sum, right_sum, cross_sum)
def max_subarray(arr):
return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)
print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")
これにより、最初に配列が 2 つの半分 (O(logn)) に分割され、次に最大交差部分配列を見つけるのに O(n) かかるため、時間計算量が O(nlogn) 時間に軽減されます
Kadane のアルゴリズム: エレガントな O(n) ソリューション
統計学者の Jay Kadane はコードを見て、Shamos のソリューションがソリューションの一部として隣接制約を使用していないことをすぐに特定しました。
これが彼が気づいたことです
- 配列に負の数値のみが含まれる場合、空の部分配列が許可されていないと仮定すると、答えは常に配列内の単一の最大の数値になります。
- 配列に正の数値のみが含まれる場合、答えは常に配列全体を合計することになります。
- 正と負の両方の数値の配列がある場合は、配列を段階的に走査できます。どこかの時点で、調べている数値がその前の数値の合計よりも大きい場合、解には前の数値を含めることはできません。したがって、これまでに発生した最大合計を追跡しながら、現在の数値から新しい合計を開始します。
maxSubArray(nums):
# avoiding type errors or index out of bounds errors
if nums is None or len(nums) == 0:
return 0
max_sum = nums[0] # max sum can't be smaller than any given element
curr_sum = 0
# Kadane's algorithm
for num in nums:
curr_sum = max(num, curr_sum + num)
max_sum = max(curr_sum, max_sum)
return max_sum
このアルゴリズムの気に入っている点は、他の多くの問題に適用できることです。これらの LeetCode の問題を解決するためにそれを調整してみてください:
1 と 0
最大合計円形サブ配列
最小サイズのサブ配列合計
最大昇順サブ配列合計
最大積サブ配列
連続部分配列の合計
最大交互合計サブアレイ (プレミアム)
K 以下の長方形の最大合計
以上が最大部分配列問題と kadane アルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

