幅優先検索 (BFS)

グラフの幅優先検索では、レベルごとに頂点を訪問します。最初のレベルは開始頂点で構成されます。次の各レベルは、前のレベルの頂点に隣接する頂点で構成されます。グラフの幅優先走査は、ツリー走査で説明したツリーの幅優先走査に似ています。ツリーの幅優先走査では、ノードはレベルごとにアクセスされます。最初にルートがアクセスされ、次にルートのすべての子がアクセスされ、次にルートの孫がアクセスされます。同様に、グラフの幅優先検索では、最初に頂点を訪問し、次にその頂点に隣接するすべての頂点を訪問し、次にそれらの頂点に隣接するすべての頂点を訪問する、というように続きます。各頂点が 1 回だけ訪問されるようにするため、すでに訪問されている頂点はスキップされます。

幅優先検索アルゴリズム

グラフの頂点 v から開始する幅優先検索のアルゴリズムは、以下のコードで説明されています。

入力: G = (V, E) および開始頂点 v
出力: v
をルートとする BFS ツリー 1 ツリー bfs(頂点 v) {
2 訪問する頂点を格納するための空のキューを作成します。
3 v をキューに追加します;
4 マーク v が訪問しました;
5
6 while (キューは空ではありません) {
7 頂点、たとえば u をキューからデキューします。
8 通過した頂点のリストに u を追加します。
あなたたちの隣人ごとに 9
w がまだ訪問されていない場合は 10 {
11 w をキューに追加します;
12 u をツリー内の w の親として設定します;
13 マークを訪問しました;
14 }
15 }
16 }

下図 (a) のグラフを考えてみましょう。頂点 0 から幅優先検索を開始するとします。下の図 (b) に示すように、最初に 0 を訪問し、次にその隣接する頂点 1、2、および 3 をすべて訪問します。頂点 1 には、0、2、および 4 という 3 つの近傍があります。0 と 2 はすでに訪問されているため、次の図 (c) に示すように、ここでは 4 だけを訪問します。頂点 2 には 3 つの近傍、0、1、および 3 があり、これらはすべて訪問済みです。頂点 3 には 3 つの近傍、0、2、および 4 があり、これらはすべて訪問されています。頂点 4 には 2 つの隣接ノード 1 と 3 があり、これらはすべて訪問済みです。したがって、検索は終了します。

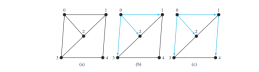
各エッジと各頂点は 1 回だけ訪問されるため、bfs メソッドの時間計算量は O(|E| + |V|) です。ここで、| E| はエッジの数を示し、|V| は頂点の数を示します。

幅優先検索の実装

bfs(int v) メソッドは、Graph インターフェースで定義され、AbstractGraph.java クラスに実装されます (197 ～ 222 行目)。これは、頂点 v をルートとする Tree クラスのインスタンスを返します。このメソッドは、検索された頂点をリスト searchOrder (198 行目) に保存し、各頂点の親を配列 parent (199 行目) に保存し、キューのリンク リストを使用します (行 199)。 203–204)、isVisited 配列を使用して頂点が訪問されたかどうかを示します (207 行目)。検索は頂点 v から開始されます。 v は 206 行目でキューに追加され、訪問済みとしてマークされます (207 行目)。このメソッドはキュー内の各頂点 u を検査し (210 行目)、それを searchOrder に追加します (211 行目)。このメソッドは、u の未訪問の各ネイバー e.v をキューに追加し (214 行目)、その親を u に設定し (215 行目)、訪問済みとしてマークします。 (行 216).

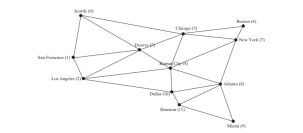
以下のコードは、シカゴから始まる上図のグラフの BFS を表示するテスト プログラムを提供します。

public class TestBFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph<string> graph = new UnweightedGraph(vertices, edges);
        AbstractGraph<string>.Tree bfs = graph.bfs(graph.getIndex("Chicago"));

        java.util.List<integer> searchOrders = bfs.getSearchOrder();
        System.out.println(bfs.getNumberOfVerticesFound() + " vertices are searched in this BFS order:");
        for(int i = 0; i 



<p>12 個の頂点が次の順序で検索されます:<br>
 シカゴ シアトル デンバー カンザスシティ ボストン ニューヨーク<br>
 サンフランシスコ ロサンゼルス アトランタ ダラス マイアミ ヒューストン<br>
シアトルの親はシカゴです<br>
サンフランシスコの親はシアトルです<br>
ロサンゼルスの親はデンバーです<br>
デンバーの親はシカゴです<br>
カンザスシティの親はシカゴです<br>
ボストンの親はシカゴです<br>
ニューヨークの親はシカゴです<br>
アトランタの親はカンザスシティです<br>
マイアミの親はアトランタです<br>
ダラスの親はカンザスシティです<br>
ヒューストンの親はアトランタです</p>

<h2>
  
  
  BFS のアプリケーション
</h2>

<p>DFS によって解決される問題の多くは、BFS を使用しても解決できます。具体的には、BFS を使用して次の問題を解決できます。</p>
<ul>
<li>グラフが接続されているかどうかを検出します。グラフ内の任意の 2 つの頂点間にパスがある場合、グラフは接続されています。</li>
<li>2 つの頂点間にパスがあるかどうかを検出します。</li>
<li>2 つの頂点間の最短経路を見つけます。ルートと BFS ツリー内の任意のノード間のパスが、ルートとノード間の最短パスであることを証明できます。</li>
<li>接続されているすべてのコンポーネントを検索します。連結コンポーネントは、頂点のすべてのペアがパスによって接続されている最大連結部分グラフです。</li>
<li>グラフに周期があるかどうかを検出します。</li>
<li>グラフ内のサイクルを見つけます。</li>
<li>グラフが 2 部であるかどうかをテストします。 (同じセット内の頂点間にエッジが存在しないように、グラフの頂点を 2 つの互いに素なセットに分割できる場合、グラフは 2 部構成です。)</li>
</ul>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172324339470608.png?x-oss-process=image/resize,p_40" class="lazy" alt="Breadth-First Search (BFS)"></p>


          

            
        </integer></string></string>

以上が幅優先検索 (BFS)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。