
Die AIxiv-Kolumne ist eine Kolumne, in der diese Website akademische und technische Inhalte veröffentlicht. In den letzten Jahren sind in der AIxiv-Kolumne dieser Website mehr als 2.000 Berichte eingegangen, die Spitzenlabore großer Universitäten und Unternehmen auf der ganzen Welt abdecken und so den akademischen Austausch und die Verbreitung wirksam fördern. Wenn Sie hervorragende Arbeiten haben, die Sie teilen möchten, können Sie gerne einen Beitrag leisten oder uns für die Berichterstattung kontaktieren. E-Mail-Adresse: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
Les auteurs de cet article sont Zhang Junpeng, Ren Qihan et Zhang Quanshi. Parmi eux, Zhang Junpeng est un futur doctorant de Zhang Quanshi et Ren Qihan est un doctorant de Zhang Quanshi. Cet article passe d'abord brièvement en revue le "Système théorique d'interprétabilité des interactions équivalentes" (20 articles CCF-A et ICLR), et sur cette base, déduit et prédit rigoureusement les performances des réseaux de neurones dans la dynamique changements de sa représentation conceptuelle et de sa généralisation au cours du processus de formation, c'est-à-dire que, dans une certaine mesure, nous pouvons expliquer la généralisation du réseau neuronal à tout moment au cours du processus de formation et ses causes profondes internes. Depuis longtemps, notre équipe réfléchit à une question ultime dans le domaine de l'interprétabilité, à savoir Quel est le premier principe dans le domaine de l'interprétabilité ? Les soi-disant premiers principes ne disposent pas actuellement d’un cadre largement accepté. Il n’existe aucun moyen au monde de définir progressivement un tel modèle. Nous devons mettre en avant un grand nombre d'exigences axiomatiques dans un nouveau système théorique et proposer une théorie capable d'expliquer avec précision et rigueur le mécanisme interne des réseaux de neurones sous différents angles. Un système théorique capable d'expliquer rigoureusement tous les aspects des réseaux de neurones est appelé « premiers principes ». Si vous faites vraiment de la « science » avec rigueur, alors le premier principe ne doit pas être aussi simple qu'on l'imagine, mais un système complexe qui nécessite des recherches et une prise en compte de tous les aspects de l'apprentissage profond. Bien sûr, si vous n’êtes pas subjectivement disposé à le faire ou si vous ne croyez pas qu’une théorie doit être suffisamment rigoureuse, la recherche deviendra alors des millions de fois plus facile. Tout comme le modèle standard de la physique doit être plus compliqué que les lois de Newton, selon le chemin que vous souhaitez emprunter.
Dans cette direction, notre équipe a construit indépendamment le «
Système théorique d'interprétabilité des interactions équivalentes » indépendamment à partir de zéro, et sur la base de cette théorie, a expliqué le mécanisme intrinsèque des réseaux de neurones sous trois perspectives. 1. Base théorique de l'explication sémantique : prouver mathématiquement si la logique décisionnelle du réseau neuronal peut être entièrement couverte (entièrement expliquée) par une petite quantité de logique symbolique. "Prouver si la logique décisionnelle des réseaux de neurones peut être expliquée clairement par une logique symbolique limitée"Cette proposition est la proposition fondamentale pour expliquer les réseaux de neurones. Si cette proposition est falsifiée, fondamentalement parlant, l’interprétabilité des réseaux neuronaux sera sans espoir, et tous les algorithmes interprétatifs ne peuvent fournir que des interprétations approximatives, mais ne peuvent pas couvrir avec précision toute la logique décisionnelle. Heureusement, nous avons trouvé trois conditions communes de robustesse orientée vers l'occlusion que les réseaux de neurones peuvent satisfaire dans la plupart des applications, et avons prouvé mathématiquement que la logique de décision des réseaux de neurones qui satisfait à ces trois conditions peut être écrite symboliquement comme un concept d'interaction. Voir https://zhuanlan.zhihu.com/p/693747946
2. Trouver les causes profondes prouvables et vérifiables derrière les indicateurs de performance : combiner la généralisation et la robustesse du réseau neuronal La cause profonde des indicateurs de performance ultimes. telles que les performances sont décomposées en quelques logiques détaillées. L'interprétation des performances des réseaux de neurones (robustesse, généralisation) est un autre enjeu important dans le domaine de l'interprétabilité des réseaux de neurones. Cependant, il est généralement admis que les performances des réseaux neuronaux sont une description du réseau neuronal dans son ensemble, et que les réseaux neuronaux ne peuvent pas démanteler leurs jugements de classification en petites quantités concrètes de logique décisionnelle comme les humains. À cet égard, nous donnons une perspective différente : établir une relation mathématique entre les indicateurs de performance et les interactions concrètes. Nous avons prouvé que 1. la complexité des interactions équivalentes peut directement déterminer la robustesse/transférabilité contradictoire des réseaux de neurones, 2. la complexité des interactions détermine la capacité de représentation des réseaux de neurones, 3. et explique la capacité de généralisation des réseaux de neurones [ 1], et 4. Expliquer le goulot d'étranglement de la représentation des réseaux de neurones.
Voir 1 : https://zhuanlan.zhihu.com/p/369883667
-
Voir 2 : https://zhuanlan.zhihu.com/p/361686461
-
Voir 3 : https://zhuanlan.zhihu.com/p/704760363
-
Voir 4 : https://zhuanlan.zhihu.com/p/468569001
3. Algorithme d'apprentissage en profondeur d'ingénierie unifié . En raison du manque de support théorique de base, la plupart des algorithmes d’apprentissage profond actuels sont empiriques et techniques. Les premiers principes dans le domaine de l’explicabilité devraient être capables d’entreprendre la tâche de résumer la grande quantité d’expérience en ingénierie des générations précédentes en lois scientifiques. Dans le cadre du système théorique d'interprétabilité des interactions équivalentes, notre équipe a prouvé que la nature informatique de 14 algorithmes différents d'attribution d'importance d'entrée peut être mathématiquement unifiée sous la forme de redistribution des interactions. En outre, nous avons également unifié 12 algorithmes pour améliorer la transférabilité contradictoire et prouvé qu'un mécanisme commun à tous les algorithmes visant à améliorer la transférabilité contradictoire consiste à réduire l'effet d'interaction entre les perturbations contradictoires, réalisant ainsi la plupart des capacités d'ingénierie dans le sens de l'interprétabilité théorique des réseaux neuronaux. condensation des algorithmes.
- 1を参照: https://zhuanlan.zhihu.com/p/610774894
- 2を参照: https://zhuanlan.zhihu.com/p/546433296
同等のインタラクティブ解釈可能性理論システムの下で、私たちのチームは、以前の研究で 20 件の CCF-A および機械学習のトップカンファレンス ICLR 論文を発表することに成功し、理論的および実験的に上記の質問に完全に答えました。 この Zhihu の記事では、上記の理論的枠組みに沿って、ニューラル ネットワークのトレーニング プロセス中に変化する一般化ルールを正確に説明したいと考えています。 2 つの論文が関係しています。
- 1.Junpeng Zhang、Qing Li、Liang Lin、Quanshi Zhang、「相互作用の 2 相ダイナミクスが過適合特徴を学習する DNN の開始点を説明する」、arXiv: 2405.10262
- 2.Qihan Ren、Yang Xu、Junpeng Zhang、Yue Xin、Dongrui Liu、Quanshi Zhang、「シンボリック インタラクションを学習する DNN のダイナミクスに向けて」、arXiv:2407.19198

Figure 1 : Diagramme schématique du phénomène en deux étapes. Dans la première étape, le réseau neuronal élimine progressivement les interactions d'ordre moyen et élevé et apprend les interactions d'ordre inférieur ; dans la deuxième étape, le réseau neuronal modélise progressivement les interactions d'ordre croissant ; Lorsque l'écart de perte entre la perte de test et la perte de formation commence à augmenter au cours du processus de formation du réseau neuronal, le réseau neuronal entre dans la deuxième étape de la formation. Nous espérons proposer une nouvelle théorie dans le cadre d'interaction équivalent pour prédire avec précision le nombre, la complexité et les changements de généralisation des concepts d'interaction appris par le réseau neuronal à chaque instant. (illustré sur la figure 1). Plus précisément, nous espérons prouver deux conclusions. Premièrement, sur la base de la preuve précédente (la logique décisionnelle d'un réseau de neurones peut être strictement déconstruite et exprimée comme la somme de l'utilité de dizaines de concepts interactifs), en déduit en outre rigoureusement que pendant tout le processus de formation , le réseau neuronal Le processus dynamique de changements dans l'utilitaire d'interaction modélisé -
C'est-à-dire que la théorie doit prédire avec précision les changements dans la distribution des concepts d'interaction modélisés par le réseau neuronal à différentes étapes de formation - pour en déduire quelles interactions seront utilisé à quel moment Appris . Deuxièmement, recherchez des preuves suffisantes pour prouver que les règles changeantes de la complexité d'interaction dérivée
reflètent objectivement les règles changeantes de la généralisation du réseau neuronal tout au long du cycle de formation. Pour résumer les deux points ci-dessus, nous espérons expliquer en profondeur les causes profondes intrinsèques des changements de généralisation des réseaux de neurones.
Relation avec les prédécesseurs : Bien sûr, tout le monde peut d'abord penser au noyau tangent neuronal (NTK) [2], mais le noyau tangent neuronal ne résout que la courbe de changement de paramètre, et ne peut pas aller plus loin. Le niveau de logique décisionnelle n'établit pas de relation entre la représentation conceptuelle de la modélisation des réseaux neuronaux et sa généralisation. L'analyse de la généralisation reste toujours au niveau de l'analyse de l'espace des fonctionnalités, et il n'y a aucun lien entre [la logique conceptuelle symbolisée] et [ logique conceptuelle symbolisée]. Une relation stricte s’établit entre généralisabilité]. 3. Deux contextes de recherche majeurs Incompréhension 1 : La représentation principale du réseau neuronal est « l'interaction équivalente », et non les paramètres et la structure du réseau neuronal. Analyser les réseaux de neurones uniquement à partir du niveau structurel est une mauvaise compréhension de la représentation fondamentale de la généralisation des réseaux de neurones. À l’heure actuelle, la plupart des recherches sur la généralisation des réseaux neuronaux se concentrent principalement sur la structure, les caractéristiques et les données des réseaux neuronaux. Les gens croient que différentes structures de réseaux neuronaux correspondent naturellement à différentes fonctions et présentent naturellement des performances différentes. Cependant, en fait, comme le montre la figure 2, la différence de structure n'est qu'une forme superficielle de représentation du réseau neuronal. À l'exception des réseaux de neurones présentant des défauts évidents qui ont un impact significatif sur les performances, tous les autres réseaux de neurones dotés de structures différentes pouvant atteindre des performances SOTA modélisent souvent des représentations d'interaction équivalentes similaires, c'est-à-dire que les réseaux de neurones hautes performances avec des structures différentes sont équivalents aux représentations interactives. conduisent souvent au même objectif à travers des approches différentes [3, 4]. Bien que les caractéristiques internes du réseau neuronal soient complexes et chaotiques, bien que les vecteurs de caractéristiques modélisés par différents réseaux neuronaux soient très différents, et bien que les neurones individuels du réseau neuronal modélisent souvent une sémantique relativement confuse (pas une sémantique strictement claire), en ce qui concerne le réseau neuronal. réseau dans son ensemble, nous prouvons théoriquement que les relations d'interaction modélisées par le réseau de neurones sont clairsemées et symboliques (plutôt que la rareté des caractéristiques, voir le chapitre « 4. Définition de l'interaction » pour plus de détails), et sont orientées vers la même tâche Des réseaux neuronaux disparates modélisent souvent des interactions similaires. Figure 2 : Les interactions équivalentes modélisées par des réseaux de neurones de structures différentes conduisent souvent au même objectif. Pour une même phrase d’entrée, deux réseaux de neurones complètement différents ciblant la même tâche modélisent souvent des interactions similaires. En raison des différents paramètres et échantillons d'entraînement des différents réseaux de neurones, aucun neurone des deux réseaux de neurones n'a une correspondance stricte un à un dans la représentation, et chaque neurone modélise souvent différents modèles de mélange sémantique. En revanche, comme analysé dans le paragraphe précédent, les représentations interactives modélisées par les réseaux de neurones sont en réalité invariantes dans différentes représentations de réseaux de neurones. Par conséquent, nous avons des raisons de croire que la représentation fondamentale des réseaux de neurones est une interaction équivalente, plutôt que son support (les paramètres et les échantillons d'apprentissage peuvent représenter le premier principe de la représentation des connaissances (théorème de parcimonie interagie, simulateur infini, théorème de cohérence). et le phénomène consistant à atteindre la même destination par différents chemins sont présentés dans le chapitre « 4. Définition de l'interaction ». Pour une recherche détaillée, voir l'article de Zhihu ci-dessous Voir : https://zhuanlan.zhihu.com. /p/633531725 Incompréhension 2 : Le problème de généralisation des réseaux de neurones est un problème de modèle mixte, pas un vecteur dans un espace de grande dimension Comme le montre la figure 3, l'analyse de généralisation traditionnelle suppose toujours qu'un seul. L'échantillon est le tout. Un point dans un espace de grande dimension. En fait, la représentation d'un échantillon unique par un réseau neuronal se présente sous la forme d'un modèle de mélange - en fait exprimé à travers un grand nombre d'interactions différentes. La capacité de généralisation des interactions simples est plus forte que celle des interactions complexes, il n'est donc plus approprié d'utiliser un simple scalaire pour représenter généralement la capacité de généralisation de l'ensemble du réseau neuronal sur différents échantillons. Au contraire, le même réseau neuronal modélise le. des relations d'interaction de complexités différentes sur différents échantillons. Les interactions correspondent souvent à des capacités de généralisation différentes. Habituellement, les interactions d'ordre élevé (complexes) modélisées par les réseaux de neurones sont souvent difficiles à généraliser aux échantillons testés (les mêmes interactions ne seront pas déclenchées sur les échantillons testés). , représentant des représentations surajustées. , et les interactions d'ordre inférieur (simples) modélisées par les réseaux de neurones représentent souvent des représentations avec une forte généralisation, veuillez consulter [1] pour une recherche détaillée.Figure 3 : (a) L'analyse de généralisation traditionnelle suppose toujours qu'un seul échantillon dans son ensemble est un point dans un espace de grande dimension. (b) En fait, le réseau de neurones représente un échantillon unique sous la forme d'un modèle de mélange. Le réseau de neurones modélise les interactions simples (interactions généralisables) et les interactions complexes (interactions non généralisables) sur un seul échantillon. 4. Définition de l'interaction . Laissez
représenter une sortie scalaire du DNN sur l'échantillon . Pour un réseau de neurones orienté vers les tâches de classification, nous pouvons définir sa sortie scalaire sous différentes perspectives. Par exemple, pour un problème de classification multi-catégories, peut être défini comme , ou comme la sortie scalaire correspondant à la véritable étiquette de l'échantillon avant la couche softmax. Ici, représente la probabilité de classification de la vraie étiquette. De cette façon, pour chaque sous-ensemble , nous pouvons utiliser la formule suivante pour définir « l'équivalence et l'interaction » et « l'équivalence ou l'interaction » entre toutes les variables d'entrée dans  Comme le montre la figure 4(a), nous pouvons comprendre l'interaction ET ou l'interaction ci-dessus comme ceci : nous pouvons penser que l'interaction équivalente ET représente la "relation ET" entre les variables d'entrée dans
Comme le montre la figure 4(a), nous pouvons comprendre l'interaction ET ou l'interaction ci-dessus comme ceci : nous pouvons penser que l'interaction équivalente ET représente la "relation ET" entre les variables d'entrée dans  codées par le réseau neuronal. Par exemple, étant donné une phrase d’entrée
codées par le réseau neuronal. Par exemple, étant donné une phrase d’entrée  , un réseau de neurones pourrait modéliser une interaction entre
, un réseau de neurones pourrait modéliser une interaction entre  telle que
telle que  produit un utilitaire numérique qui pilote la « pluie » de sortie du réseau de neurones. Si une variable d'entrée dans
produit un utilitaire numérique qui pilote la « pluie » de sortie du réseau de neurones. Si une variable d'entrée dans  est occultée, cet utilitaire numérique sera supprimé de la sortie du réseau neuronal. De même, l'équivalence ou l'interaction
est occultée, cet utilitaire numérique sera supprimé de la sortie du réseau neuronal. De même, l'équivalence ou l'interaction  représente la « relation OU » entre les variables d'entrée au sein de
représente la « relation OU » entre les variables d'entrée au sein de  modélisée par le réseau neuronal. Par exemple, étant donné une phrase d'entrée
modélisée par le réseau neuronal. Par exemple, étant donné une phrase d'entrée  , tant qu'un mot dans
, tant qu'un mot dans  apparaît, cela pilotera la sortie du réseau neuronal pour classer les émotions négatives. L'interaction équivalente modélisée par le réseau de neurones satisfait aux trois critères axiomatiques du « concept idéal », à savoir l'ajustement infini, la parcimonie et la transférabilité inter-échantillons.
apparaît, cela pilotera la sortie du réseau neuronal pour classer les émotions négatives. L'interaction équivalente modélisée par le réseau de neurones satisfait aux trois critères axiomatiques du « concept idéal », à savoir l'ajustement infini, la parcimonie et la transférabilité inter-échantillons.
- Ajustement infini : Comme le montrent les figures 4 et 5, pour tout échantillon d'occlusion, la sortie du réseau neuronal sur l'échantillon peut être ajustée par la somme des utilités de différents concepts d'interaction. Autrement dit, nous pouvons construire un modèle logique basé sur l'interaction. Quelle que soit la manière dont nous bloquons l'échantillon d'entrée, ce modèle logique peut toujours ajuster avec précision la valeur de sortie du modèle dans n'importe quel état bloqué de l'échantillon d'entrée.
- Sparsity : Les réseaux de neurones pour les tâches de classification ne modélisent souvent qu'un petit nombre de concepts interactifs significatifs, et la plupart des concepts interactifs sont du bruit avec une utilité numérique proche de 0.
- Transférabilité entre échantillons : Les interactions sont transférables entre différents échantillons, c'est-à-dire que les concepts d'interaction significatifs modélisés par des réseaux de neurones sur différents échantillons (de la même catégorie) se chevauchent souvent beaucoup.

図 4: ニューラル ネットワークの複雑な推論ロジックは、少数の相互作用  に基づくロジック モデルによって正確に適合できます。各相互作用は、特定の入力変数セット
に基づくロジック モデルによって正確に適合できます。各相互作用は、特定の入力変数セット  をモデル化するニューラル ネットワーク間の非線形関係の尺度です。セット内の変数が同時に出現する場合にのみ、トリガーおよび相互作用し、出力
をモデル化するニューラル ネットワーク間の非線形関係の尺度です。セット内の変数が同時に出現する場合にのみ、トリガーおよび相互作用し、出力  に数値スコアを提供します。セット
に数値スコアを提供します。セット  内の変数が出現すると、トリガーまたは相互作用します。
内の変数が出現すると、トリガーまたは相互作用します。 
図 5: 任意のオクルージョン サンプルに対するニューラル ネットワークの出力は、さまざまなインタラクション概念の効用の合計によって適合できます。つまり、入力をどのようにオクルージョンするかに関係なく、インタラクションに基づいて論理モデルを構築できます。たとえば、入力ユニットで完全に異なるオクルージョン方法が与えられた場合でも、この論理モデルは、どのようなオクルージョン状態でもモデルの入力サンプルの出力値を正確に適合させることができます。 5.1 トレーニング中のニューラルネットワークのインタラクティブな変化の 2 段階の現象を発見する この Zhihu の記事では、にニューラル ネットワークの解釈可能性の分野における基本的な問題、つまり、学習プロセス中のニューラル ネットワークの汎化能力の変化を分析解析の観点から厳密に予測し、ニューラル ネットワークの過小適合から過適合への移行を正確に分析する方法です。フィッティングの動的変化プロセス全体とその背後にある根本原因。 まず、対話の次数 (複雑さ) を対話内の入力変数の数 として定義します。私たちのチームの以前の研究では、特定のサンプルのニューラル ネットワークによってモデル化された「またはとの相互作用」の複雑さが、このサンプルのニューラル ネットワークの汎化能力 [1]、つまりニューラル ネットワークの高次レベルを直接決定することがわかりました。ネットワーク モデリングでは、「AND-OR 相互作用」(多数の入力ユニット間) は一般化機能が劣る傾向がありますが、低次の「AND-OR 相互作用」(少数の入力ユニット間) は強力な汎化機能を持っています。  したがって、この研究の最初のステップは、トレーニング プロセス中のさまざまな時点でニューラル ネットワークによってモデル化された、さまざまな次数の「AND-OR 相互作用」の複雑さに対する分析的解決策を予測することです。さまざまな段階でのニューラル ネットワークの汎化能力は、さまざまな時点でのニューラル ネットワークによってモデル化されたさまざまな次数の「AND または相互作用」の分布を通じて説明されます。相互作用の汎化能力の定義とニューラルネットワーク全体の汎化能力の定義については、「5.2 ニューラルネットワークがモデル化する相互作用の順序と汎化能力の関係」の章を参照してください。 異なる次数の相互作用の強度(複雑さ)の分布を表すための 2 つの指標を提案します。具体的には、
したがって、この研究の最初のステップは、トレーニング プロセス中のさまざまな時点でニューラル ネットワークによってモデル化された、さまざまな次数の「AND-OR 相互作用」の複雑さに対する分析的解決策を予測することです。さまざまな段階でのニューラル ネットワークの汎化能力は、さまざまな時点でのニューラル ネットワークによってモデル化されたさまざまな次数の「AND または相互作用」の分布を通じて説明されます。相互作用の汎化能力の定義とニューラルネットワーク全体の汎化能力の定義については、「5.2 ニューラルネットワークがモデル化する相互作用の順序と汎化能力の関係」の章を参照してください。 異なる次数の相互作用の強度(複雑さ)の分布を表すための 2 つの指標を提案します。具体的には、
を使用して順序のすべての正の有意な相互作用の強度を測定し、を使用して順序のすべての負の有意な相互作用の強度を測定します。ここで、 と
と は有意な相互作用のセットを表し、
は有意な相互作用のセットを表し、 は有意な相互作用のしきい値を表します交流。
は有意な相互作用のしきい値を表します交流。 

 図 6: 異なるラウンドでトレーニングされたニューラル ネットワークから抽出された異なる次数相互作用の強度
図 6: 異なるラウンドでトレーニングされたニューラル ネットワークから抽出された異なる次数相互作用の強度  および
および  。異なるデータセットおよび異なるタスクでトレーニングされたさまざまなニューラル ネットワークのトレーニング プロセスには 2 段階の現象があります。最初の 2 つの選択された時点は第 1 フェーズに属し、最後の 2 つの時点は第 2 フェーズに属します。ニューラル ネットワークのトレーニング プロセスの第 2 段階に入った直後に、ニューラル ネットワークのテスト損失とトレーニング損失の間の損失ギャップが大幅に増加し始めます (最後のコラムを参照)。これは、ニューラル ネットワーク トレーニングの 2 段階の現象が、モデルの損失ギャップの変化に合わせて「調整」されていることを示しています。詳しい実験結果については論文をご覧ください。 図 6 に示すように、ニューラル ネットワークの 2 段階の現象は、具体的には次のように表されます。レベルの相互作用、高次および低次の相互作用はほとんどコード化されず、異なる次数の相互作用の分布は「紡錘型」のように見えます。ランダムな初期化パラメータを持つニューラル ネットワークが純粋なノイズをモデル化すると仮定すると、「5.4 2 段階現象の理論的証明」で、ランダムな初期化パラメータを持つニューラル ネットワークによってモデル化された異なる次数の相互作用の分布が「紡錘形」を示すことを証明しました。つまり、少数の低次および高次の相互作用のみがモデル化され、多数の中次の相互作用がモデル化されます。
。異なるデータセットおよび異なるタスクでトレーニングされたさまざまなニューラル ネットワークのトレーニング プロセスには 2 段階の現象があります。最初の 2 つの選択された時点は第 1 フェーズに属し、最後の 2 つの時点は第 2 フェーズに属します。ニューラル ネットワークのトレーニング プロセスの第 2 段階に入った直後に、ニューラル ネットワークのテスト損失とトレーニング損失の間の損失ギャップが大幅に増加し始めます (最後のコラムを参照)。これは、ニューラル ネットワーク トレーニングの 2 段階の現象が、モデルの損失ギャップの変化に合わせて「調整」されていることを示しています。詳しい実験結果については論文をご覧ください。 図 6 に示すように、ニューラル ネットワークの 2 段階の現象は、具体的には次のように表されます。レベルの相互作用、高次および低次の相互作用はほとんどコード化されず、異なる次数の相互作用の分布は「紡錘型」のように見えます。ランダムな初期化パラメータを持つニューラル ネットワークが純粋なノイズをモデル化すると仮定すると、「5.4 2 段階現象の理論的証明」で、ランダムな初期化パラメータを持つニューラル ネットワークによってモデル化された異なる次数の相互作用の分布が「紡錘形」を示すことを証明しました。つまり、少数の低次および高次の相互作用のみがモデル化され、多数の中次の相互作用がモデル化されます。 ニューラル ネットワークのトレーニング - の最初の段階では、ニューラル ネットワークによってエンコードされた高次および中次の相互作用の強度が徐々に弱まり、低次の相互作用の強度が徐々に増加します。最終的に、高次および中次の相互作用は徐々に排除され、ニューラル ネットワークは低次の相互作用のみをエンコードします。
ニューラル ネットワーク トレーニングの第 2 フェーズでは、ニューラル ネットワークによってエンコードされた相互作用の順序 (複雑さ) がトレーニング プロセス中に徐々に増加します。より複雑な相互作用を徐々に学習する過程で、ニューラル ネットワークの過剰適合のリスクも徐々に増加します。
- 上記の 2 段階の現象は、異なるタスク、異なるデータセットで異なる構造を持つニューラル ネットワークのトレーニング プロセスに広く存在します。 VGG-11/13/16 を画像データセット (CIFAR-10 データセット、MNIST データセット、CUB200-2011 データセット (写真から切り取った鳥の画像を使用) および Tiny-ImageNet データセット) と AlexNet でトレーニングしました。 SST-2 データセットで感情意味分類のために Bert-Medium/Tiny モデルをトレーニングし、3D 点群データを分類するために ShapeNet データセットで DGCNN をトレーニングしました。上の図は、異なるトレーニング エポックで異なるニューラル ネットワークによって抽出された、異なる次数の重要な相互作用の分布を示しています。私たちは、これらのニューラル ネットワークのトレーニング プロセス中に 2 段階の現象を発見しました。実験結果と詳細については、論文を参照してください。
5.2 ニューラルネットワークによってモデル化された相互作用の順序とその汎化能力の関係 私たちのチームの以前の研究では、ニューラルネットワークによってモデル化された相互作用の順序とその汎化能力の関係、つまり、高次の相互作用は、低次の相互作用よりも汎化能力が劣ります [1]。特定の相互作用の一般化可能性は明確に定義されています。相互作用がトレーニング サンプルとテスト サンプルの両方でニューラル ネットワークによって頻繁にモデル化される場合、この相互作用は優れた一般化能力を持っています。この Zhihu の記事では、高次の相互作用には汎化能力が低く、低次の相互作用には強い汎化能力があることを証明する 2 つの実験が紹介されています。
実験 1: 異なるデータセットでトレーニングされた異なるニューラル ネットワークによってモデル化された相互作用の一般化を観察します。ここでは、テスト セットによってトリガーされたインタラクションの分布とトレーニング セットによってトリガーされたインタラクションの分布の間の Jaccard 類似度を使用して、インタラクションの一般化を測定します。具体的には、 入力変数を含む入力サンプル
入力変数を含む入力サンプル  が与えられた場合、入力サンプル
が与えられた場合、入力サンプル  から抽出された
から抽出された  次の交互作用を
次の交互作用を  ベクトル化します。ここで、
ベクトル化します。ここで、  は
は 
 次の相互作用を表します。次に、分類タスクでカテゴリ
次の相互作用を表します。次に、分類タスクでカテゴリ  を持つすべてのサンプルから抽出された次数
を持つすべてのサンプルから抽出された次数  の平均交互作用ベクトルを計算します。これは
の平均交互作用ベクトルを計算します。これは  として表されます。ここで、
として表されます。ここで、 はカテゴリ
はカテゴリ  を持つサンプルのセットを表します。次に、トレーニング サンプルから抽出された次数
を持つサンプルのセットを表します。次に、トレーニング サンプルから抽出された次数  の平均相互作用ベクトル
の平均相互作用ベクトル  と、テスト サンプルから抽出された次数
と、テスト サンプルから抽出された次数  の平均相互作用ベクトル
の平均相互作用ベクトル  の間の Jaccard 類似度を計算し、分類タスクでカテゴリ
の間の Jaccard 類似度を計算し、分類タスクでカテゴリ  を持つサンプルの を測定します。順序相互作用の一般化能力、つまり
を持つサンプルの を測定します。順序相互作用の一般化能力、つまり 
 ここで、
ここで、 と
と  は、Jaccard 類似度を計算するために、2 つの
は、Jaccard 類似度を計算するために、2 つの  次元の相互作用ベクトルを 2 つの 次元の非負ベクトルに投影します。特定の次数のインタラクションについて、このインタラクションの次数が一般に大きな Jaccard 類似性を示す場合、このインタラクションの次数が強い一般化能力を持っていることを意味します。
次元の相互作用ベクトルを 2 つの 次元の非負ベクトルに投影します。特定の次数のインタラクションについて、このインタラクションの次数が一般に大きな Jaccard 類似性を示す場合、このインタラクションの次数が強い一般化能力を持っていることを意味します。  私たちは、さまざまな次数の相互作用を計算する実験を行いました
私たちは、さまざまな次数の相互作用を計算する実験を行いました 。 MNIST データセットでトレーニングされた LeNet、CIFAR-10 データセットでトレーニングされた VGG-11、CUB200-2011 データセットでトレーニングされた VGG-13、Tiny-ImageNet データセットでトレーニングされた AlexNet をテストしました。計算コストを削減するために、上位 10 カテゴリの平均 Jaccard 類似度のみを計算しました。図 7 に示すように、インタラクションの次数が増加するにつれて、インタラクションの Jaccard 類似性は減少し続けます。したがって、これは、高次の相互作用が低次の相互作用よりも劣った汎化能力を持っていることを証明します。図 7: トレーニング サンプルとテスト サンプルから抽出されたインタラクション間の Jaccard の類似性。低次の相互作用の比較的高い Jaccard 類似性は、低次の相互作用が強力な汎化能力を持っていることを示しています。
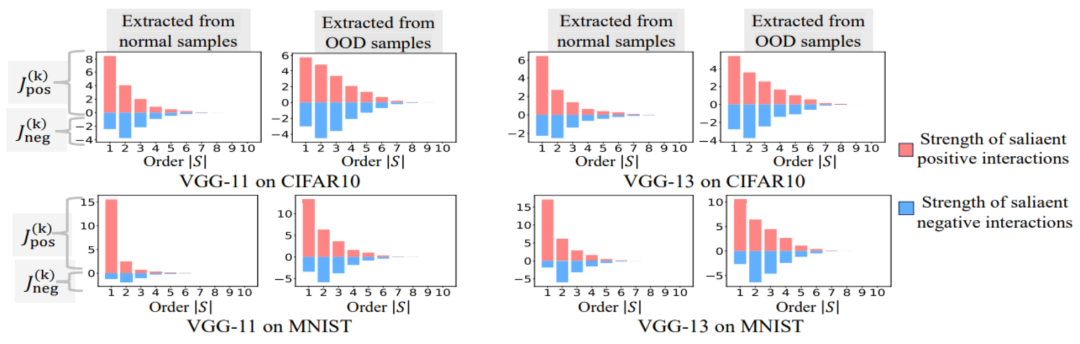
。 MNIST データセットでトレーニングされた LeNet、CIFAR-10 データセットでトレーニングされた VGG-11、CUB200-2011 データセットでトレーニングされた VGG-13、Tiny-ImageNet データセットでトレーニングされた AlexNet をテストしました。計算コストを削減するために、上位 10 カテゴリの平均 Jaccard 類似度のみを計算しました。図 7 に示すように、インタラクションの次数が増加するにつれて、インタラクションの Jaccard 類似性は減少し続けます。したがって、これは、高次の相互作用が低次の相互作用よりも劣った汎化能力を持っていることを証明します。図 7: トレーニング サンプルとテスト サンプルから抽出されたインタラクション間の Jaccard の類似性。低次の相互作用の比較的高い Jaccard 類似性は、低次の相互作用が強力な汎化能力を持っていることを示しています。  Experiment 2: Vergleich der Verteilung von Interaktionen, die durch neuronale Netze an normalen Proben und OOD-Proben modelliert wurden. Wir verglichen Interaktionen, die aus normalen Proben extrahiert wurden, mit Interaktionen, die aus Proben außerhalb der Verteilung (OOD) extrahiert wurden, um zu untersuchen, ob das neuronale Netzwerk mehr Interaktionen höherer Ordnung auf OOD-Proben modelliert. Wir haben die Klassifizierungsbezeichnungen einer kleinen Anzahl von Trainingsbeispielen auf falsche Bezeichnungen gesetzt. Auf diese Weise können die Originalproben im Datensatz als normale Proben betrachtet werden, während einige Proben mit falschen Bezeichnungen OOD-Proben entsprechen und diese OOD-Proben zu einer Überanpassung des neuronalen Netzwerks führen können. Wir haben VGG-11 und VGG-13 anhand des MNIST-Datensatzes bzw. des CIFAR-10-Datensatzes trainiert. Abbildung 8 vergleicht die Verteilung der aus normalen Proben extrahierten Interaktionen mit der Verteilung der aus OOD-Proben extrahierten Interaktionen. Wir stellen fest, dass VGG-11 und VGG-13 komplexere Wechselwirkungen (Wechselwirkungen höherer Ordnung) bei der Klassifizierung von OOD-Proben modellieren, während Wechselwirkungen niedrigerer Ordnung bei der Klassifizierung normaler Proben verwendet werden. Dies bestätigt, dass die Generalisierungsfähigkeit von Wechselwirkungen höherer Ordnung im Allgemeinen schwächer ist als die von Wechselwirkungen niedrigerer Ordnung.
Experiment 2: Vergleich der Verteilung von Interaktionen, die durch neuronale Netze an normalen Proben und OOD-Proben modelliert wurden. Wir verglichen Interaktionen, die aus normalen Proben extrahiert wurden, mit Interaktionen, die aus Proben außerhalb der Verteilung (OOD) extrahiert wurden, um zu untersuchen, ob das neuronale Netzwerk mehr Interaktionen höherer Ordnung auf OOD-Proben modelliert. Wir haben die Klassifizierungsbezeichnungen einer kleinen Anzahl von Trainingsbeispielen auf falsche Bezeichnungen gesetzt. Auf diese Weise können die Originalproben im Datensatz als normale Proben betrachtet werden, während einige Proben mit falschen Bezeichnungen OOD-Proben entsprechen und diese OOD-Proben zu einer Überanpassung des neuronalen Netzwerks führen können. Wir haben VGG-11 und VGG-13 anhand des MNIST-Datensatzes bzw. des CIFAR-10-Datensatzes trainiert. Abbildung 8 vergleicht die Verteilung der aus normalen Proben extrahierten Interaktionen mit der Verteilung der aus OOD-Proben extrahierten Interaktionen. Wir stellen fest, dass VGG-11 und VGG-13 komplexere Wechselwirkungen (Wechselwirkungen höherer Ordnung) bei der Klassifizierung von OOD-Proben modellieren, während Wechselwirkungen niedrigerer Ordnung bei der Klassifizierung normaler Proben verwendet werden. Dies bestätigt, dass die Generalisierungsfähigkeit von Wechselwirkungen höherer Ordnung im Allgemeinen schwächer ist als die von Wechselwirkungen niedrigerer Ordnung. 
常 Figure 8: Compare interactions extracted from normal samples and interactions extracted from distribution (OOD) samples. Neural networks typically model higher-order interactions on OOD samples.
5.3 The two-stage phenomenon and the change in loss gap during the neural network training process are relatively consistent
We found that the above two-stage phenomenon can fully represent the generalization dynamics of the neural network. A very interesting phenomenon is that the two-stage phenomenon in the neural network training process and the changes in the loss gap of the neural network in the test set and training set are aligned in time. The loss gap between training loss and test loss is the most widely used metric to measure the degree of model overfitting. Figure 6 shows the curves of the loss gap between the test loss and the training loss of the training project for different neural networks, and also shows the interaction distributions extracted from the neural networks at different training epochs. We found that when the loss gap between the test loss and the training loss begins to increase during the neural network training process, the neural network happens to enter the second stage of training. This shows that the two-stage phenomenon of neural network training is "aligned" in time with changes in the model loss gap. We can understand the above phenomenon this way: before the training process starts, the interactions modeled by the initialized neural network all represent random noise, and the distribution of interactions of different orders looks like a "spindle". In the first stage of neural network training, the neural network gradually eliminates intermediate and high-order interactions and learns the simplest (lowest-order) interactions. Then, in the second stage of neural network training, the neural network models interactions of increasing order. Since our two experiments in the chapter "5.2 The relationship between the order of interaction modeled by neural networks and its generalization ability" have verified that high-order interactions usually have worse generalization capabilities than low-order interactions, we can think In the second stage of neural network training, the DNN first learns the interactions with the strongest generalization ability, and then gradually moves to more complex interactions with weaker generalization ability. Eventually some neural networks gradually overfit and encode a large number of mid- and high-order interactions.
5.4 Theoretically prove the two-stage phenomenon Theoretically prove the two-stage phenomenon of the neural network training process is divided into three parts. In the first part, we need to prove that the randomly initialized neural network before the training process starts The distribution of modeled interactions shows a “spindle shape”, that is, high-order and low-order interactions are rarely modeled, and mid-order interactions are mainly modeled. The second part demonstrates that the neural network models increasingly larger interactions in the second phase of training. Section 3 demonstrates that the neural network gradually eliminates mid- and high-order interactions in the first stage of training and learns the lowest-cost interactions.
1. Prove the “spindle” interaction distribution for initialization neural network modeling. Since the randomly initialized random network models noise before the training process starts, we assume that the interactions modeled by the randomly initialized neural network obey the normal distribution with mean
and variance . Under the above assumptions, we were able to show that the distribution of the intensity sum of interactions modeled by the initialized neural network exhibits a “spindle shape”, i.e., it rarely models high-order and low-order interactions and mainly models mid-order interactions. 2. Prove the dynamic process of interactive changes in the second stage of neural network training. Before entering the formal certification, we need to do the following preparatory work. First, we follow the approach of [5, 6] and rewrite the inference of the neural network  on a specific sample as a weighted sum of different interaction trigger functions:
on a specific sample as a weighted sum of different interaction trigger functions:  where
where  is a scalar weight, satisfying
is a scalar weight, satisfying  . The function
. The function  is an interactive trigger function, which satisfies
is an interactive trigger function, which satisfies  on any occlusion sample
on any occlusion sample  . The specific form of function
. The specific form of function  can be derived from Taylor expansion. Please refer to the paper and will not be described here.
can be derived from Taylor expansion. Please refer to the paper and will not be described here.
According to the above rewritten form, The learning of the neural network on a specific sample can be approximately regarded as the learning of the weight  of the interactive trigger function. Furthermore, the laboratory's preliminary work [3] found that different neural networks fully trained on the same task tend to model similar interactions, so we can regard the learning of neural networks as a series of potential ground truth interactions. fitting. Therefore, the interaction modeled by the neural network when it is trained to convergence can be seen as the solution obtained when minimizing the following objective function:
of the interactive trigger function. Furthermore, the laboratory's preliminary work [3] found that different neural networks fully trained on the same task tend to model similar interactions, so we can regard the learning of neural networks as a series of potential ground truth interactions. fitting. Therefore, the interaction modeled by the neural network when it is trained to convergence can be seen as the solution obtained when minimizing the following objective function:  where
where  represents a series of potential ground truth interactions that the neural network needs to fit.
represents a series of potential ground truth interactions that the neural network needs to fit.  and
and  respectively represent the vector obtained by putting together all the weights and the vector obtained by putting together the values of all interaction trigger functions.
respectively represent the vector obtained by putting together all the weights and the vector obtained by putting together the values of all interaction trigger functions.
Unfortunately, although the above modeling can obtain the interaction when the neural network is trained to convergence, it cannot well describe the dynamic process of learning interaction during the neural network training process. Here we introduce our core hypothesis: We assume that the parameters of the initialized neural network contain a large amount of noise, and the magnitude of these noises gradually becomes smaller during the training process. Furthermore, noise on the parameters will lead to noise on the interaction trigger function , and this noise increases exponentially with the interaction order (it has been experimentally observed and verified in [5]). We model the learning of neural networks with noise as follows: 
where noise  satisfies
satisfies  . And as the training proceeds, the variance of the noise
. And as the training proceeds, the variance of the noise  gradually becomes smaller. By minimizing the above loss function for a given noise level
gradually becomes smaller. By minimizing the above loss function for a given noise level  , the analytical solution of the optimal interaction weight
, the analytical solution of the optimal interaction weight  can be obtained, as shown in the theorem in the figure below.
can be obtained, as shown in the theorem in the figure below.

We found that as training progresses (i.e., the noise magnitude  becomes smaller), the ratio of low- and medium-order interaction strengths to high-order interaction strengths gradually decreases (as shown in the theorem below). This explains the phenomenon in which the neural network gradually learns higher-order interactions during the second phase of training.
becomes smaller), the ratio of low- and medium-order interaction strengths to high-order interaction strengths gradually decreases (as shown in the theorem below). This explains the phenomenon in which the neural network gradually learns higher-order interactions during the second phase of training. 
In addition, we have further experimentally verified the above conclusion. Given a sample with n input units, the metric  , where
, where  , can be used to approximately measure the ratio of the strength of the kth-order interaction to the k+1th-order interaction. In the figure below, we can find that under different number of input units n and different orders k, the ratio will gradually decrease as
, can be used to approximately measure the ratio of the strength of the kth-order interaction to the k+1th-order interaction. In the figure below, we can find that under different number of input units n and different orders k, the ratio will gradually decrease as  decreases.
decreases. 
Figure 9 : Sous un nombre différent d'unités d'entrée n et un ordre k différent, le rapport entre l'interaction d'ordre k et la force d'interaction d'ordre k+1 changera avec le niveau de bruit  diminuera progressivement . Cela montre qu'à mesure que l'entraînement progresse (c'est-à-dire que
diminuera progressivement . Cela montre qu'à mesure que l'entraînement progresse (c'est-à-dire que  devient progressivement plus petit), le rapport entre l'intensité d'interaction d'ordre inférieur et l'intensité d'interaction d'ordre élevé devient progressivement plus petit et le réseau neuronal apprend progressivement les interactions d'ordre supérieur. Enfin, nous avons comparé la distribution des valeurs d'interaction théoriques à chaque ordre sous différents niveaux de bruit
devient progressivement plus petit), le rapport entre l'intensité d'interaction d'ordre inférieur et l'intensité d'interaction d'ordre élevé devient progressivement plus petit et le réseau neuronal apprend progressivement les interactions d'ordre supérieur. Enfin, nous avons comparé la distribution des valeurs d'interaction théoriques à chaque ordre sous différents niveaux de bruit 
 avec la distribution de chaque ordre d'interaction au cours du processus de formation réel
avec la distribution de chaque ordre d'interaction au cours du processus de formation réel  et avons constaté que le théorie La distribution des interactions peut bien prédire la distribution de l'intensité des interactions à chaque instant de l'entraînement réel.
et avons constaté que le théorie La distribution des interactions peut bien prédire la distribution de l'intensité des interactions à chaque instant de l'entraînement réel. 
 그림 10: 이론적 상호 작용 분포
그림 10: 이론적 상호 작용 분포  (파란색 히스토그램)과 실제 상호 작용 분포
(파란색 히스토그램)과 실제 상호 작용 분포  (주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요. 3. 신경망 훈련의 첫 번째 단계에서 대화형 변화의 동적 프로세스를 증명합니다. 훈련의 두 번째 단계에서 상호 작용의 동적 변화를 소음
(주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요. 3. 신경망 훈련의 첫 번째 단계에서 대화형 변화의 동적 프로세스를 증명합니다. 훈련의 두 번째 단계에서 상호 작용의 동적 변화를 소음 
 이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다. 갈 길이 멀다. 우리 팀은 이 이론을 더 많은 측면에서 확고히 하고 등가 상호 작용이 상징적 설명이라는 것을 엄격하게 증명할 수 있기를 바랍니다. , 신경망 표현의 병목 현상을 입증하고 신경망의 마이그레이션 저항성을 향상시키는 12가지 방법을 통합하고 14가지 중요도 추정 방법을 설명하는 동시에 신경망의 일반화 및 견고성을 설명할 수 있습니다. 나중에 이론적인 시스템을 더욱 개선하기 위해 더욱 탄탄한 작업을 하도록 하겠습니다. [1] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan 및 Quanshi Zhang이 대화형 개념을 사용하여 DNS의 일반화 능력을 설명합니다., 2024 [2] Arthur Jacot, Franck Gabriel, 신경 탄젠트 커널: 신경망의 수렴 및 일반화. NeurIPS, 2018[3] 신경망은 실제로 ICML을 인코딩합니까? , 2023[4] Wen Shen, Lei Cheng, Yuxiao Yang, Mingjie Li 및 Quanshi Zhang. 대규모 언어 모델의 추론 논리를 상징적 개념으로 풀 수 있습니까?[5] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou 및 Quanshi Zhang. ICML, 2023[6] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang 및 Quanshi. Zhang. 다양한 복잡성의 개념을 학습하기 위한 심층 신경망의 어려움. NeurIPS, 2023
이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다. 갈 길이 멀다. 우리 팀은 이 이론을 더 많은 측면에서 확고히 하고 등가 상호 작용이 상징적 설명이라는 것을 엄격하게 증명할 수 있기를 바랍니다. , 신경망 표현의 병목 현상을 입증하고 신경망의 마이그레이션 저항성을 향상시키는 12가지 방법을 통합하고 14가지 중요도 추정 방법을 설명하는 동시에 신경망의 일반화 및 견고성을 설명할 수 있습니다. 나중에 이론적인 시스템을 더욱 개선하기 위해 더욱 탄탄한 작업을 하도록 하겠습니다. [1] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan 및 Quanshi Zhang이 대화형 개념을 사용하여 DNS의 일반화 능력을 설명합니다., 2024 [2] Arthur Jacot, Franck Gabriel, 신경 탄젠트 커널: 신경망의 수렴 및 일반화. NeurIPS, 2018[3] 신경망은 실제로 ICML을 인코딩합니까? , 2023[4] Wen Shen, Lei Cheng, Yuxiao Yang, Mingjie Li 및 Quanshi Zhang. 대규모 언어 모델의 추론 논리를 상징적 개념으로 풀 수 있습니까?[5] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou 및 Quanshi Zhang. ICML, 2023[6] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang 및 Quanshi. Zhang. 다양한 복잡성의 개념을 학습하기 위한 심층 신경망의 어려움. NeurIPS, 2023
등가 상호 작용 이론 시스템
[1] Huiqi Deng, Na Zou, Mengnan Du, Weifu Chen, Guocan Feng, Ziwei Yang, Zheyang Li, Quanshi Zhang. Taylor 상호 작용을 통해 14가지 사후 기여 분석 방법 통합. 패턴 분석 및 기계 지능(IEEE T-PAMI)에 대한 IEEE 트랜잭션, 2024.
[2] Xu Cheng, Lei Cheng , Zhaoran Peng, Yang Xu, Tian Han 및 Quanshi Zhang. ICML, 2024.
[3] Qihan Ren, Jiayang Gao, Wen Shen 및 Quanshi Zhang. AI 모델에서 희소 상호 작용 프리미티브의 출현 증명, 2024.
[4] Lu Chen, Siyu Lou, Benhao Huang 및 Quanshi Zhang ICLR에서 일반화 가능한 상호 작용 프리미티브 정의 및 추출, 2024.
[5] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan 및 Quanshi Zhang. 대화형 개념을 사용하여 DNN의 일반화 기능 설명, 2024.
[ 6 ] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang 및 Quanshi Zhang. 다양한 복잡성의 개념을 학습하기 위한 심층 신경망의 어려움, 2023.
[7] Quanshi Zhang, Jie Ren, Ge Huang, Ruiming Cao, Ying Nian Wu und Song-Chun Zhu. Gewinnung interpretierbarer AOG-Darstellungen aus Faltungsnetzwerken über aktive Fragebeantwortung (IEEE T -PAMI), 2020.
[8] Xin Wang, Jie Ren, Shuyun Lin, Xiangming Zhu, Yisen Wang und Quanshi Zhang. Ein einheitlicher Ansatz zur Interpretation und Steigerung der kontradiktorischen Übertragbarkeit [9] Hao Zhang, Sen Li, Yinchao Ma, Mingjie Li, Yichen Xie und Quanshi Zhang . Kodiert ein neuronales Netzwerk wirklich ein symbolisches Konzept? . ICML, 2023.
[12] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou und Quanshi Zhang. Vermeiden Sie die Kodierung störungsempfindlicher und komplexer Konzepte ] Jie Ren, Mingjie Li, Qirui Chen, Huiqi Deng und Quanshi Zhang: Definition und Quantifizierung der Entstehung spärlicher Konzepte in DNNs, 2023.
[14] Jie Ren, Mingjie Li, Meng Zhou, Shih- Han Chan und Quanshi Zhang. Auf dem Weg zur theoretischen Analyse der Transformationskomplexität von ReLU-DNNs, 2022.
[15] Jie Ren, Die Zhang, Yisen Wang, Lu Chen, Zhanpeng Zhou, Yiting Chen, Xu Cheng, Xin Wang, Meng Zhou, Jie Shi und Quanshi Zhang. Eine einheitliche spieltheoretische Interpretation der gegnerischen Robustheit DNNs für die 3D-Punktwolkenverarbeitung.
[17] Xin Wang, Shuyun Lin, Hao Zhang, Yufei Zhu und Quanshi Zhang. ] Wen Shen, Zhihua Wei, Shikun Huang, Binbin Zhang, Panyue Chen, Ping Zhao und Quanshi Zhang: Interpreting Utilities of Network Architectures for 3D Point Cloud Processing, 2021.
[19] Hao Zhang, Yichen Xie , Longjie Zheng, Die Zhang und Quanshi Zhang. Interpreting Multivariate Shapley Interactions in DNNs, 2021. Mengyue Wu und Quanshi Zhang. Aufbau interpretierbarer Interaktionsbäume für Deep NLP-Modelle, 2021.
以上が説明可能性に関する究極の問題は、最初の説明は何かということです。 20 の CCF-A+ICLR 論文が答えを提供しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。


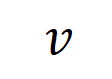
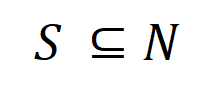 codées par le réseau neuronal. Par exemple, étant donné une phrase d’entrée
codées par le réseau neuronal. Par exemple, étant donné une phrase d’entrée 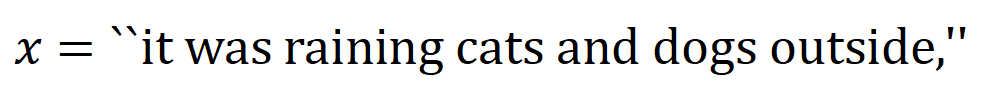 , un réseau de neurones pourrait modéliser une interaction entre
, un réseau de neurones pourrait modéliser une interaction entre 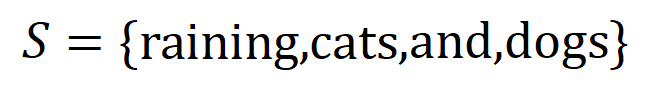 telle que
telle que 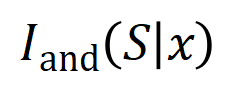 produit un utilitaire numérique qui pilote la « pluie » de sortie du réseau de neurones. Si une variable d'entrée dans
produit un utilitaire numérique qui pilote la « pluie » de sortie du réseau de neurones. Si une variable d'entrée dans 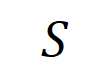 est occultée, cet utilitaire numérique sera supprimé de la sortie du réseau neuronal. De même, l'équivalence ou l'interaction
est occultée, cet utilitaire numérique sera supprimé de la sortie du réseau neuronal. De même, l'équivalence ou l'interaction 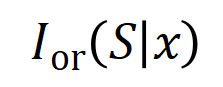 représente la « relation OU » entre les variables d'entrée au sein de
représente la « relation OU » entre les variables d'entrée au sein de  modélisée par le réseau neuronal. Par exemple, étant donné une phrase d'entrée
modélisée par le réseau neuronal. Par exemple, étant donné une phrase d'entrée 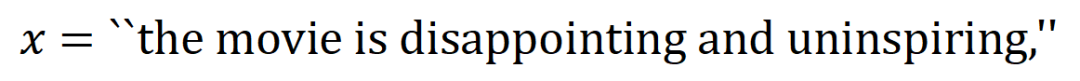 , tant qu'un mot dans
, tant qu'un mot dans 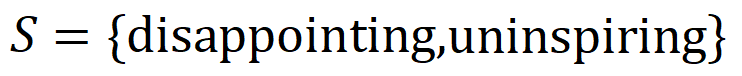 apparaît, cela pilotera la sortie du réseau neuronal pour classer les émotions négatives.
apparaît, cela pilotera la sortie du réseau neuronal pour classer les émotions négatives. 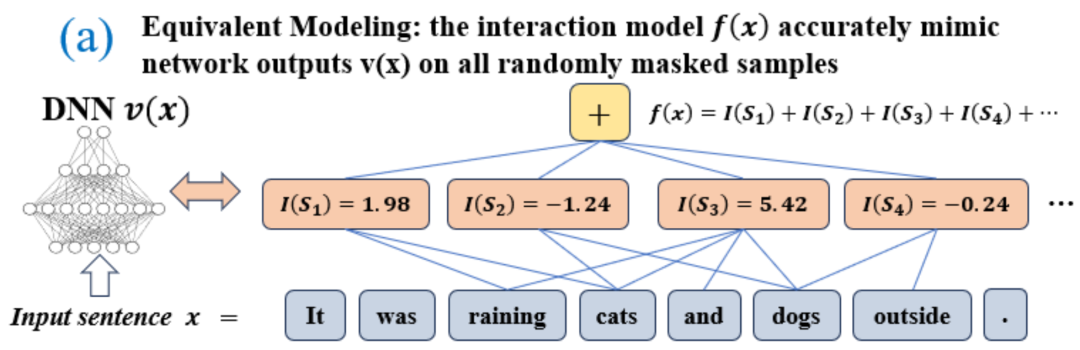
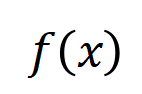 に基づくロジック モデルによって正確に適合できます。各相互作用は、特定の入力変数セット
に基づくロジック モデルによって正確に適合できます。各相互作用は、特定の入力変数セット 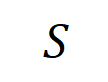 をモデル化するニューラル ネットワーク間の非線形関係の尺度です。セット内の変数が同時に出現する場合にのみ、トリガーおよび相互作用し、出力
をモデル化するニューラル ネットワーク間の非線形関係の尺度です。セット内の変数が同時に出現する場合にのみ、トリガーおよび相互作用し、出力 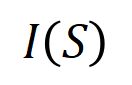 に数値スコアを提供します。セット
に数値スコアを提供します。セット  内の変数が出現すると、トリガーまたは相互作用します。
内の変数が出現すると、トリガーまたは相互作用します。 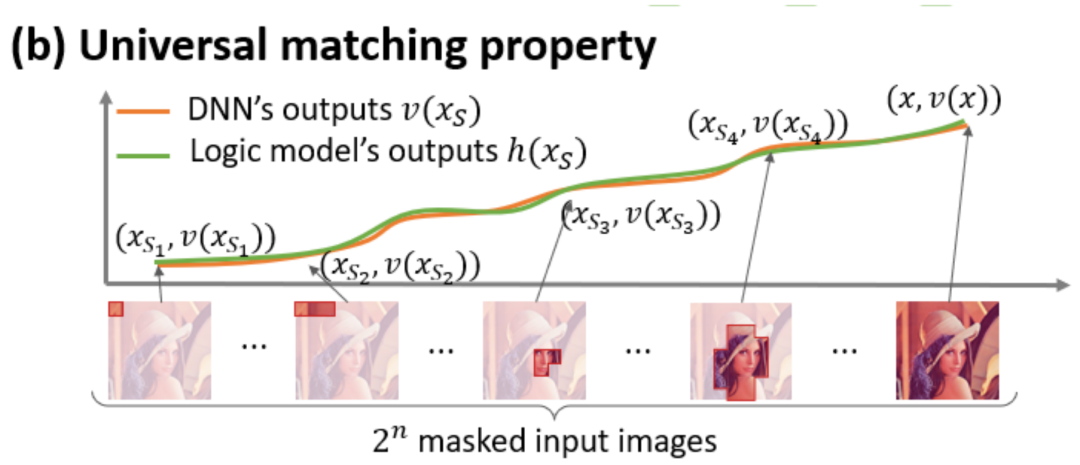
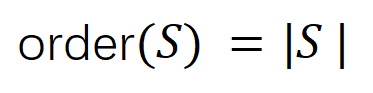
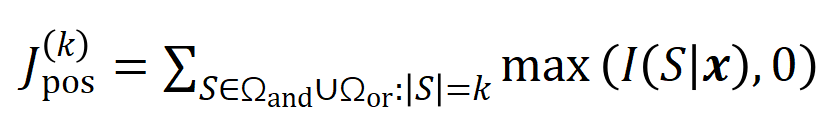 と
と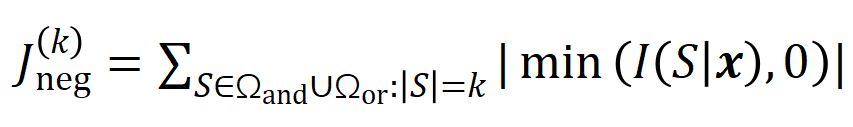 は有意な相互作用のセットを表し、
は有意な相互作用のセットを表し、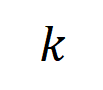 は有意な相互作用のしきい値を表します交流。
は有意な相互作用のしきい値を表します交流。 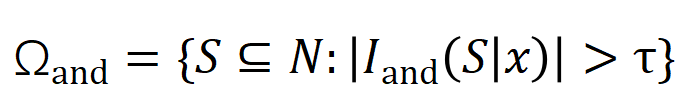
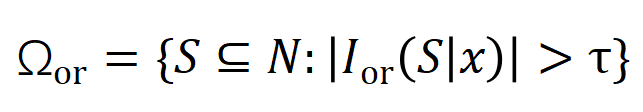

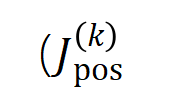 および
および 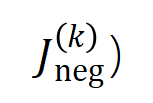 。異なるデータセットおよび異なるタスクでトレーニングされたさまざまなニューラル ネットワークのトレーニング プロセスには 2 段階の現象があります。最初の 2 つの選択された時点は第 1 フェーズに属し、最後の 2 つの時点は第 2 フェーズに属します。ニューラル ネットワークのトレーニング プロセスの第 2 段階に入った直後に、ニューラル ネットワークのテスト損失とトレーニング損失の間の損失ギャップが大幅に増加し始めます (最後のコラムを参照)。これは、ニューラル ネットワーク トレーニングの 2 段階の現象が、モデルの損失ギャップの変化に合わせて「調整」されていることを示しています。詳しい実験結果については論文をご覧ください。
。異なるデータセットおよび異なるタスクでトレーニングされたさまざまなニューラル ネットワークのトレーニング プロセスには 2 段階の現象があります。最初の 2 つの選択された時点は第 1 フェーズに属し、最後の 2 つの時点は第 2 フェーズに属します。ニューラル ネットワークのトレーニング プロセスの第 2 段階に入った直後に、ニューラル ネットワークのテスト損失とトレーニング損失の間の損失ギャップが大幅に増加し始めます (最後のコラムを参照)。これは、ニューラル ネットワーク トレーニングの 2 段階の現象が、モデルの損失ギャップの変化に合わせて「調整」されていることを示しています。詳しい実験結果については論文をご覧ください。 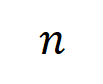 入力変数を含む入力サンプル
入力変数を含む入力サンプル  が与えられた場合、入力サンプル
が与えられた場合、入力サンプル  から抽出された
から抽出された  次の交互作用を
次の交互作用を 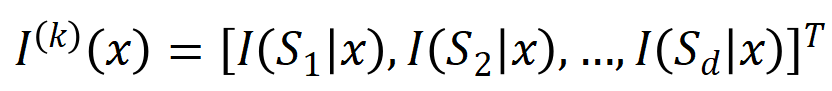 ベクトル化します。ここで、
ベクトル化します。ここで、 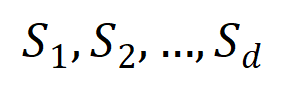 は
は 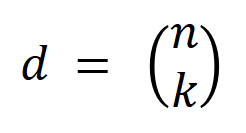
 次の相互作用を表します。次に、分類タスクでカテゴリ
次の相互作用を表します。次に、分類タスクでカテゴリ  を持つすべてのサンプルから抽出された次数
を持つすべてのサンプルから抽出された次数  の平均交互作用ベクトルを計算します。これは
の平均交互作用ベクトルを計算します。これは 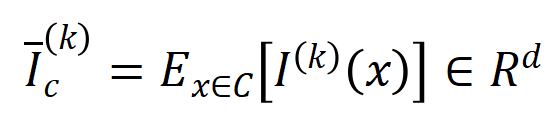 として表されます。ここで、
として表されます。ここで、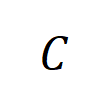 はカテゴリ
はカテゴリ  を持つサンプルのセットを表します。次に、トレーニング サンプルから抽出された次数
を持つサンプルのセットを表します。次に、トレーニング サンプルから抽出された次数 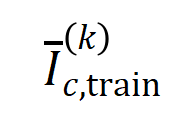 の平均相互作用ベクトル
の平均相互作用ベクトル  と、テスト サンプルから抽出された次数
と、テスト サンプルから抽出された次数 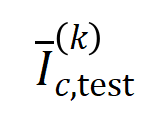 の平均相互作用ベクトル
の平均相互作用ベクトル  の間の Jaccard 類似度を計算し、分類タスクでカテゴリ
の間の Jaccard 類似度を計算し、分類タスクでカテゴリ  を持つサンプルの
を持つサンプルの 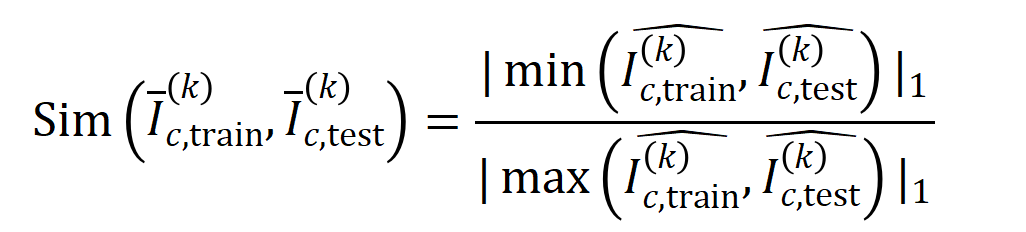
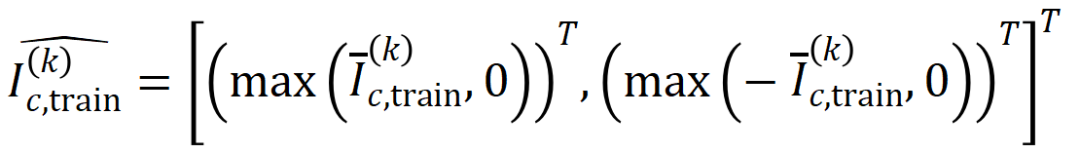 ここで、
ここで、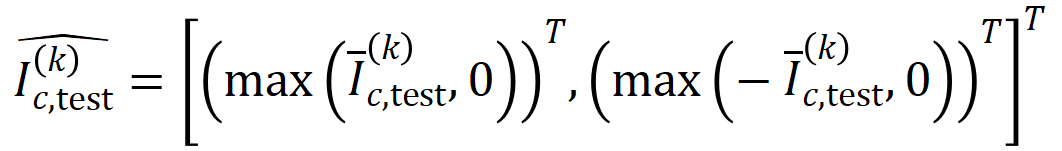 と
と 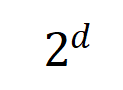 は、Jaccard 類似度を計算するために、2 つの
は、Jaccard 類似度を計算するために、2 つの 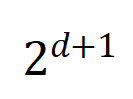 次元の相互作用ベクトルを 2 つの
次元の相互作用ベクトルを 2 つの 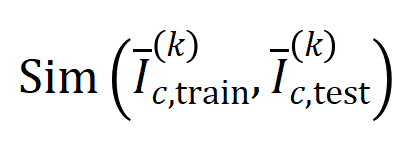 私たちは、さまざまな次数の相互作用を計算する実験を行いました
私たちは、さまざまな次数の相互作用を計算する実験を行いました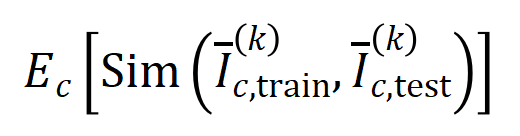 。 MNIST データセットでトレーニングされた LeNet、CIFAR-10 データセットでトレーニングされた VGG-11、CUB200-2011 データセットでトレーニングされた VGG-13、Tiny-ImageNet データセットでトレーニングされた AlexNet をテストしました。計算コストを削減するために、上位 10 カテゴリの平均 Jaccard 類似度のみを計算しました
。 MNIST データセットでトレーニングされた LeNet、CIFAR-10 データセットでトレーニングされた VGG-11、CUB200-2011 データセットでトレーニングされた VGG-13、Tiny-ImageNet データセットでトレーニングされた AlexNet をテストしました。計算コストを削減するために、上位 10 カテゴリの平均 Jaccard 類似度のみを計算しました
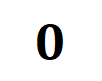
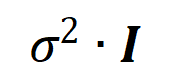
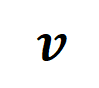 on a specific sample as a weighted sum of different interaction trigger functions:
on a specific sample as a weighted sum of different interaction trigger functions:  where
where  is a scalar weight, satisfying
is a scalar weight, satisfying  . The function
. The function  is an interactive trigger function, which satisfies
is an interactive trigger function, which satisfies  on any occlusion sample
on any occlusion sample  . The specific form of function
. The specific form of function  can be derived from Taylor expansion. Please refer to the paper and will not be described here.
can be derived from Taylor expansion. Please refer to the paper and will not be described here. 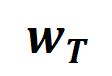 of the interactive trigger function. Furthermore, the laboratory's preliminary work [3] found that different neural networks fully trained on the same task tend to model similar interactions, so we can regard the learning of neural networks as a series of potential ground truth interactions. fitting. Therefore, the interaction modeled by the neural network when it is trained to convergence can be seen as the solution obtained when minimizing the following objective function:
of the interactive trigger function. Furthermore, the laboratory's preliminary work [3] found that different neural networks fully trained on the same task tend to model similar interactions, so we can regard the learning of neural networks as a series of potential ground truth interactions. fitting. Therefore, the interaction modeled by the neural network when it is trained to convergence can be seen as the solution obtained when minimizing the following objective function:  where
where  represents a series of potential ground truth interactions that the neural network needs to fit.
represents a series of potential ground truth interactions that the neural network needs to fit.  and
and 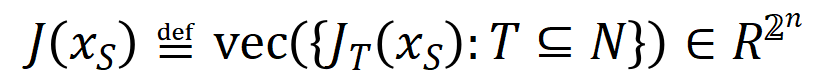 respectively represent the vector obtained by putting together all the weights and the vector obtained by putting together the values of all interaction trigger functions.
respectively represent the vector obtained by putting together all the weights and the vector obtained by putting together the values of all interaction trigger functions. 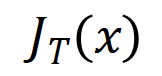
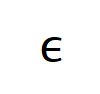 satisfies
satisfies 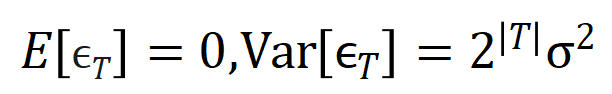 . And as the training proceeds, the variance of the noise
. And as the training proceeds, the variance of the noise 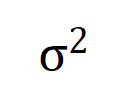 gradually becomes smaller.
gradually becomes smaller.  , the analytical solution of the optimal interaction weight
, the analytical solution of the optimal interaction weight  can be obtained, as shown in the theorem in the figure below.
can be obtained, as shown in the theorem in the figure below. 
 becomes smaller), the ratio of low- and medium-order interaction strengths to high-order interaction strengths gradually decreases (as shown in the theorem below). This explains the phenomenon in which the neural network gradually learns higher-order interactions during the second phase of training.
becomes smaller), the ratio of low- and medium-order interaction strengths to high-order interaction strengths gradually decreases (as shown in the theorem below). This explains the phenomenon in which the neural network gradually learns higher-order interactions during the second phase of training. 
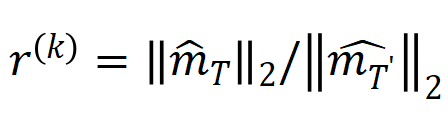 , where
, where 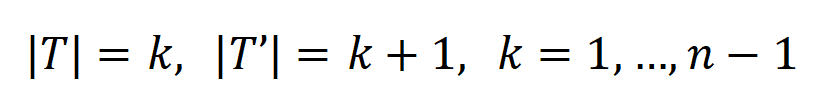 , can be used to approximately measure the ratio of the strength of the kth-order interaction to the k+1th-order interaction. In the figure below, we can find that under different number of input units n and different orders k, the ratio will gradually decrease as
, can be used to approximately measure the ratio of the strength of the kth-order interaction to the k+1th-order interaction. In the figure below, we can find that under different number of input units n and different orders k, the ratio will gradually decrease as  decreases.
decreases. 
 diminuera progressivement . Cela montre qu'à mesure que l'entraînement progresse (c'est-à-dire que
diminuera progressivement . Cela montre qu'à mesure que l'entraînement progresse (c'est-à-dire que  devient progressivement plus petit), le rapport entre l'intensité d'interaction d'ordre inférieur et l'intensité d'interaction d'ordre élevé devient progressivement plus petit et le réseau neuronal apprend progressivement les interactions d'ordre supérieur.
devient progressivement plus petit), le rapport entre l'intensité d'interaction d'ordre inférieur et l'intensité d'interaction d'ordre élevé devient progressivement plus petit et le réseau neuronal apprend progressivement les interactions d'ordre supérieur. 
 avec la distribution de chaque ordre d'interaction au cours du processus de formation réel
avec la distribution de chaque ordre d'interaction au cours du processus de formation réel  et avons constaté que le théorie La distribution des interactions peut bien prédire la distribution de l'intensité des interactions à chaque instant de l'entraînement réel.
et avons constaté que le théorie La distribution des interactions peut bien prédire la distribution de l'intensité des interactions à chaque instant de l'entraînement réel. 

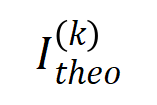 (파란색 히스토그램)과 실제 상호 작용 분포
(파란색 히스토그램)과 실제 상호 작용 분포 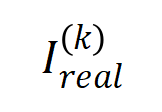 (주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요.
(주황색 히스토그램) 비교. 이론적 상호작용 분포는 훈련의 두 번째 단계에서 다양한 시점의 실제 상호작용 분포를 잘 예측하고 일치시킵니다. 더 많은 결과를 보려면 논문을 참조하세요. 
 이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다.
이 점차 감소할 때 가중치 의 최적 솔루션의 변화로 설명할 수 있다면 첫 번째 단계는 초기 무작위 상호작용은 점차적으로 최적의 솔루션으로 수렴됩니다. 
