ホームページ >ウェブフロントエンド >jsチュートリアル >Javascript を使用したアルゴリズムの旅 - バブルソート
Javascript を使用したアルゴリズムの旅 - バブルソート
- PHPzオリジナル
- 2024-07-29 06:30:53511ブラウズ
バブルソートとは何ですか?
バブル ソートは、コンピューター サイエンスにおける最も単純なソート アルゴリズムの 1 つです。反復のたびに小さな要素がリストの先頭に「バブル」する様子にちなんで名付けられたこのツールは、並べ替えアルゴリズムの基本を教えるための優れたツールです。大規模なデータセットにとっては最も効率的ではありませんが、そのシンプルさは、並べ替えアルゴリズムがどのように機能するかを理解するための優れた出発点になります。
バブルソートの仕組み
バブル ソートは、リストを繰り返しステップ実行し、隣接する要素を比較し、順序が間違っている場合は入れ替えることによって機能します。このプロセスは、スワップが必要なくなるまで繰り返され、リストがソートされたことが示されます。
段階的に詳しく説明します:
- 配列の最初の要素から始めます。
- 次の要素と比較します。
- 最初の要素が 2 番目の要素より大きい場合は、それらを交換します。
- 次の要素に移動し、配列の最後に到達するまで手順 2 ~ 3 を繰り返します。
- 交換が行われた場合は、最初からプロセスを繰り返します。
- フルパスでスワップが行われなかった場合、配列はソートされます。
このプロセスを視覚化してみましょう:
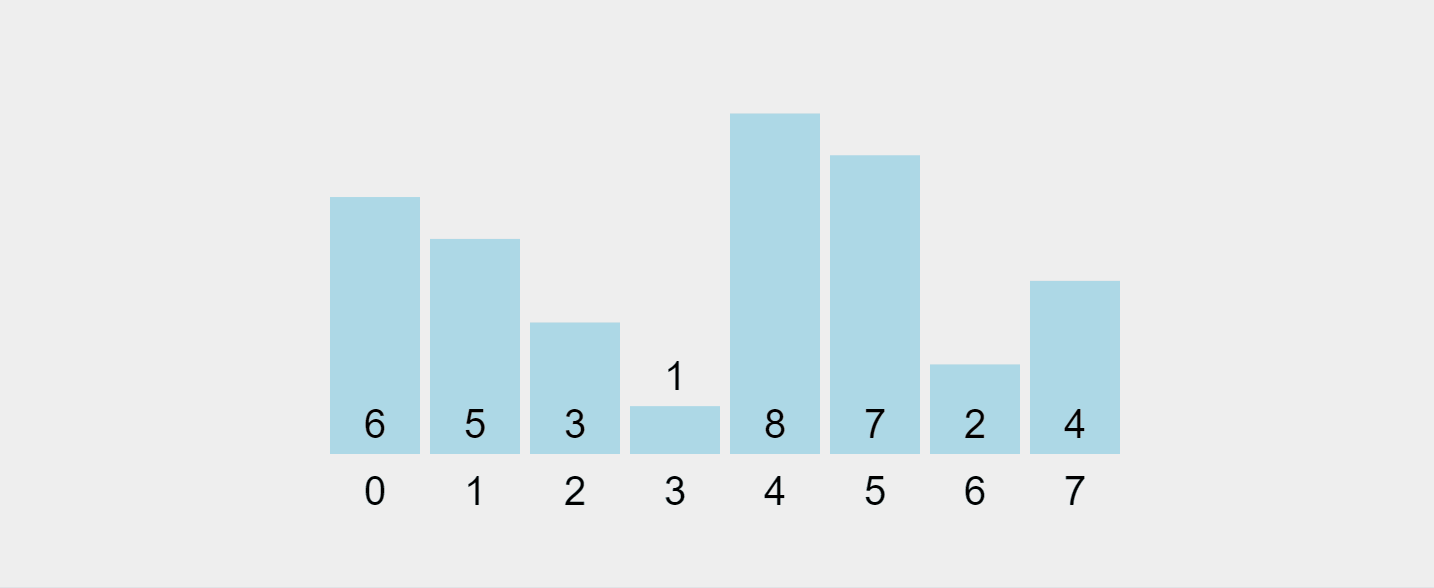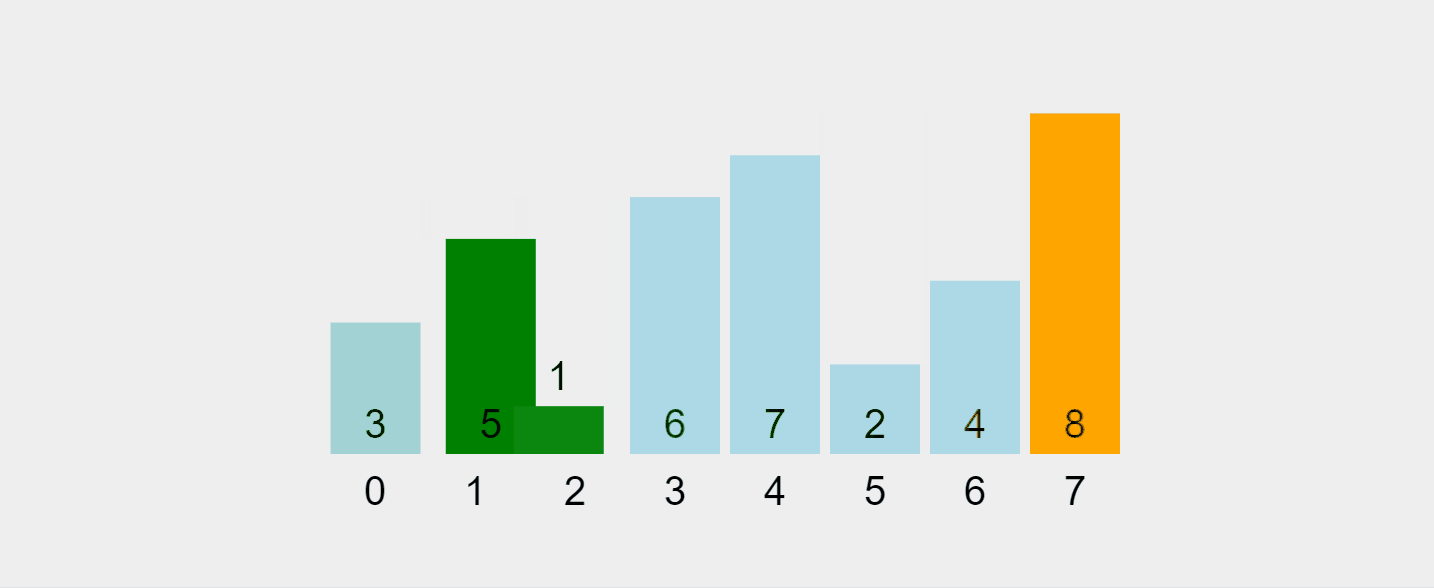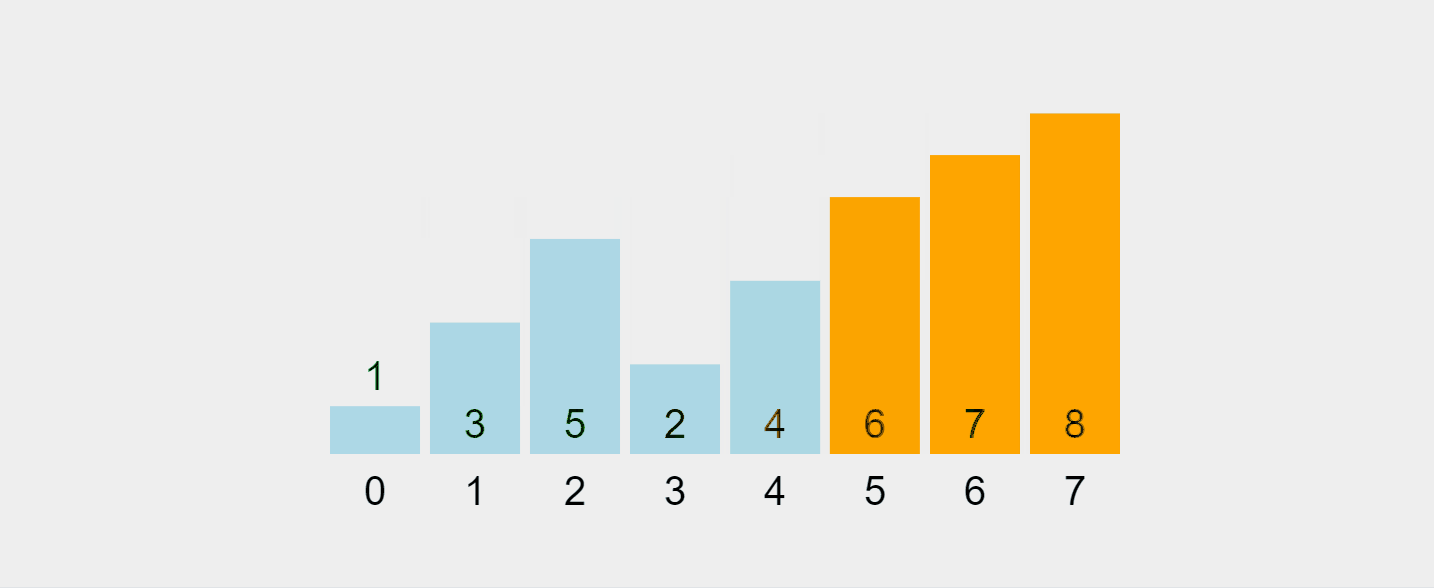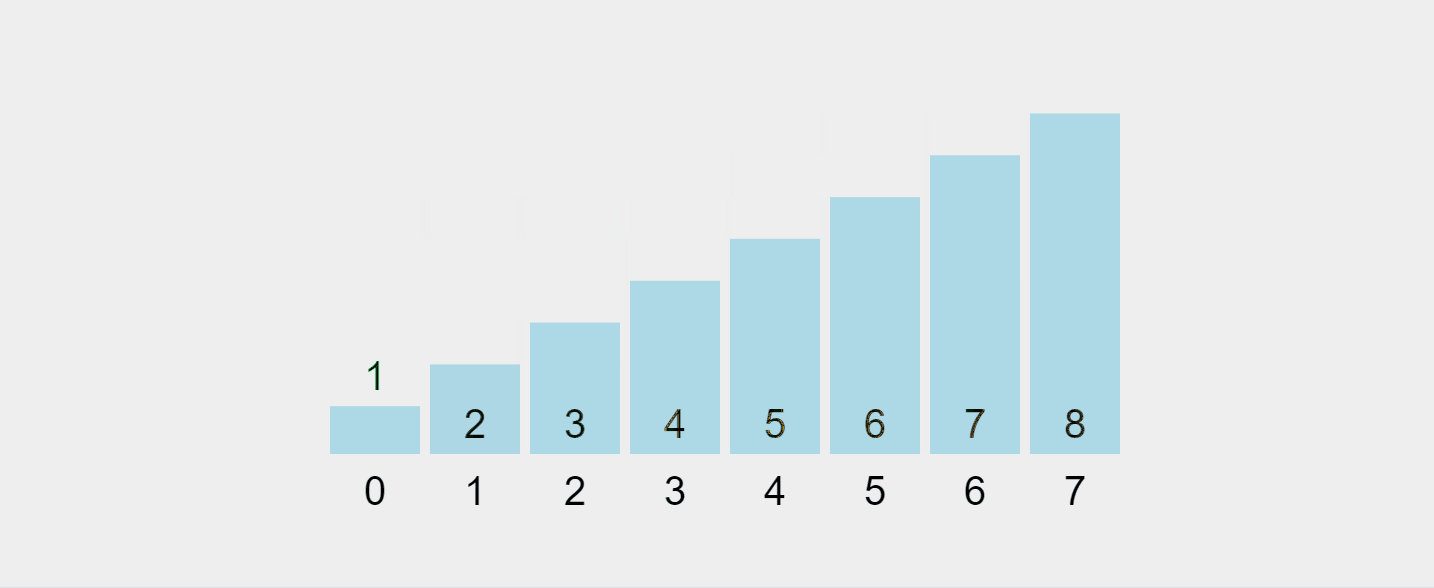
https://visualgo.net/en/sorting から録画した GIF
JavaScript でのバブル ソートの実装
それぞれ最適化レベルを上げながら、JavaScript でのバブル ソートの 3 つの実装を調べてみましょう。
基本的な実装 (v1)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Inner loop: compare adjacent elements
for (let j = 0; j < list.length - 1; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
}
}
}
// Return the sorted list
return list;
}
この基本的な実装では、ネストされたループを使用して、隣接する要素を比較および交換します。外側のループは配列内で十分なパスを実行することを保証し、内側のループは比較と交換を実行します。
最適化された実装 (v2)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Flag to check if any swaps occurred in this pass
let swapped = false;
// Inner loop: compare adjacent elements
for (let j = 0; j < list.length - 1; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
// Set the swapped flag to true
swapped = true;
}
}
// If no swaps occurred in this pass, the list is sorted
if (!swapped) {
break; // Exit the outer loop early
}
}
// Return the sorted list
return list;
}
このバージョンでは、パス内でスワップが行われたかどうかを確認するためのスワップ済みフラグが導入されています。スワップが発生しない場合、リストはすでにソートされているため、ループを早期に抜け出すことができます。
最も最適化された実装 (v3)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Flag to check if any swaps occurred in this pass
let swapped = false;
// Inner loop: compare adjacent elements
// Note: We reduce the upper bound by i in each pass
for (let j = 0; j < list.length - 1 - i; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
// Set the swapped flag to true
swapped = true;
}
}
// If no swaps occurred in this pass, the list is sorted
if (!swapped) {
break; // Exit the outer loop early
}
}
// Return the sorted list
return list;
}
この最後の最適化により、各パスで内側のループの範囲が i ずつ減少します。これは、各パスの後、ソートされていない最大の要素が配列の末尾の正しい位置に「バブルアップ」するためです。
時間と空間の複雑さの分析
バブルソートのパフォーマンス特性は次のとおりです:
-
時間計算量:
- ベストケース: O(n) - 配列がすでにソートされている場合
- 平均ケース: O(n^2)
- 最悪のケース: O(n^2) - 配列が逆順の場合
空間複雑さ: O(1) - バブル ソートはインプレース ソート アルゴリズムであり、一定量の追加メモリのみを必要とします。
クイック ソート (平均 O(n log n)) やマージ ソート (O(n log n)) などのより高度なアルゴリズムと比較して、バブル ソートの二次時間計算量により、大規模なデータセットの場合は非効率的になります。
バブルソートの長所と短所
利点:
- 理解と実装が簡単
- インプレースソート (O(1) スペース)
- 安定した並べ替えアルゴリズム
- 既にソートされたリストを検出できます
欠点:
- 大規模なデータセット (O(n^2)) では非効率的
- ほとんどソートされたデータのパフォーマンスが低い
- 過剰なスワップ操作
バブルソートを使用する場合
- 教育目的: そのシンプルさにより、基本的なアルゴリズムの概念を教えるのに最適です。
- 小さなデータセット: 非常に小さな配列の場合、複雑なアルゴリズムと比較したパフォーマンスの違いは無視できる程度である可能性があります。
- ほぼソートされたデータ: 最適化されたバージョンを使用すると、ほぼソートされたリストでかなり効率的になります。
- 限られたメモリ環境: そのインプレースの性質は、メモリが極度に制約されたシナリオで有利になる可能性があります。
カクテルソート: 改良されたバリエーション
カクテル ソートは、カクテル シェイク ソートまたは双方向バブル ソートとも呼ばれ、バブル ソートの改良版です。これはリストを両方向に走査し、要素をより効率的に正しい位置に移動するのに役立ちます。
How Cocktail Sort Works
- Start with the first element and move towards the end, swapping adjacent elements if they're in the wrong order.
- When you reach the end, start from the second-to-last element and move towards the beginning, again swapping elements as needed.
- Repeat this process, narrowing the range of elements to check with each pass, until no swaps are needed.
Cocktail Sort is particularly useful in cases where the array has elements that are initially large at the beginning and small at the end, as it can reduce the total number of passes needed compared to traditional Bubble Sort.
Here's a visualization of Cocktail Sort:
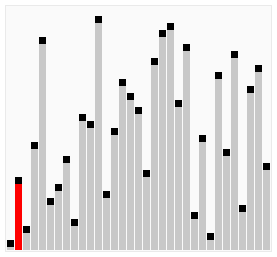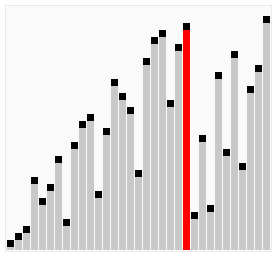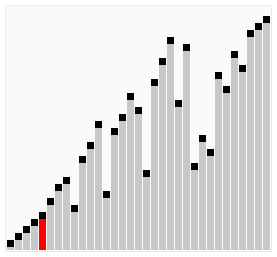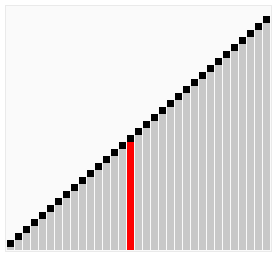
Visual from Wikipedia: https://en.wikipedia.org/wiki/Cocktail_shaker_sort
Cocktail Sort implementation in Javascript
function cocktailSort(list) {
let swapped;
// The do...while loop ensures the sorting continues until no swaps are needed
do {
// Reset the swapped flag at the beginning of each complete iteration
swapped = false;
// First pass: left to right (like standard bubble sort)
for (let i = 0; i < list.length - 1; i++) {
// If the current element is greater than the next, swap them
if (list[i] > list[i + 1]) {
[list[i], list[i + 1]] = [list[i + 1], list[i]];
// Mark that a swap occurred
swapped = true;
}
}
// If no swaps occurred in the first pass, the array is sorted
if (!swapped) {
break; // Exit the do...while loop early
}
// Reset the swapped flag for the second pass
swapped = false;
// Second pass: right to left (this is what makes it "cocktail" sort)
for (let i = list.length - 2; i >= 0; i--) {
// If the current element is greater than the next, swap them
if (list[i] > list[i + 1]) {
[list[i], list[i + 1]] = [list[i + 1], list[i]];
// Mark that a swap occurred
swapped = true;
}
}
// The loop will continue if any swaps occurred in either pass
} while (swapped);
// Return the sorted list
return list;
}
This implementation alternates between forward and backward passes through the list, potentially reducing the number of iterations needed to sort the array.
Practical Applications and Use Cases
While Bubble Sort isn't typically used in production environments for large-scale applications, it can still find use in certain scenarios:
- Educational tools: It's often used to introduce sorting algorithms and algorithm analysis in computer science education.
- Embedded systems: In systems with very limited memory, its in-place sorting can be advantageous.
- Small datasets: For sorting small lists (e.g., less than 50 elements), its simplicity might outweigh the performance benefits of more complex algorithms.
- Nearly sorted data: If data is known to be almost sorted, an optimized Bubble Sort can be reasonably efficient.
- Sorting stability requirement: When a stable sort is needed and simplicity is preferred over efficiency, Bubble Sort can be a straightforward choice.
Conclusion
Bubble Sort, despite its inefficiencies with large datasets, offers valuable insights into the world of sorting algorithms and algorithm analysis. Its straightforward approach makes it an excellent teaching tool for beginners in computer science.
Key takeaways are:
- It's simple to understand and implement.
- It has a time complexity of O(n^2), making it inefficient for large datasets.
- It's an in-place and stable sorting algorithm.
- Optimizations can improve its performance, especially for nearly sorted data.
- It's primarily used for educational purposes and in scenarios with very small datasets or limited memory.
While you're unlikely to use Bubble Sort in production code for large-scale applications, the principles behind it are fundamental to many algorithms. The process of optimizing Bubble Sort teaches valuable lessons about algorithm improvement, serving as a stepping stone to more advanced computational problem-solving.
When it comes to algorithms, there's rarely a one-size-fits-all solution. The best algorithm for a given task depends on the specific requirements, constraints, and characteristics of your data. Bubble Sort, with all its limitations, still has its place in this diverse algorithmic ecosystem.
以上がJavascript を使用したアルゴリズムの旅 - バブルソートの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

