ホームページ >テクノロジー周辺機器 >AI >TPAMI 2024 | ProCo: 無限対照ペアのロングテール対照学習
TPAMI 2024 | ProCo: 無限対照ペアのロングテール対照学習
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBオリジナル
- 2024-07-25 20:52:33570ブラウズ

AIxivコラムは、当サイトが学術的・技術的な内容を掲載するコラムです。過去数年間で、このサイトの AIxiv コラムには 2,000 件を超えるレポートが寄せられ、世界中の主要な大学や企業のトップ研究室がカバーされ、学術交流と普及を効果的に促進しています。共有したい優れた作品がある場合は、お気軽に寄稿するか、報告のために当社までご連絡ください。提出電子メール: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
この論文の筆頭著者である Du Chaoqun は、清華大学オートメーション学科の 2020 年度直接博士課程の学生です。チューターは黄高准教授です。彼は以前に清華大学物理学科で理学士号を取得しています。彼の研究対象には、ロングテール学習、半教師あり学習、転移学習などのさまざまなデータ分布におけるモデルの一般化とロバスト性の研究が含まれます。 TPAMIやICMLなど一流の国際ジャーナルや学会に論文を多数発表。
個人ホームページ: https://andy-du20.github.io
この記事では、清華大学のロングテール視覚認識に関する論文「ロングテール視覚認識のための確率的対照学習」を紹介します。 TPAMI 2024 が承認され、コードはオープンソースになりました。
この研究は、ロングテール視覚認識タスクにおける対照学習の適用に主に焦点を当てており、コントラスト損失を改善することで、無制限の数の対照ペアの対照学習を実現する新しいロングテール対照学習方法を提案します。問題を効果的に解決する 教師あり対照学習[1]は、バッチ (メモリ バンク) サイズに本質的に依存します。ロングテール視覚分類タスクに加えて、この方法はロングテール半教師あり学習、ロングテール物体検出、およびバランスのとれたデータセットでも実験され、大幅なパフォーマンスの向上が達成されました。

- 論文リンク: https://arxiv.org/pdf/2403.06726
- プロジェクトリンク: https://github.com/LeapLabTHU/ProCo
比較自己教師あり学習での学習の成功は、視覚的特徴表現の学習におけるその有効性を示しています。対照学習のパフォーマンスに影響を与える中心的な要素は、
対照ペアの数です。これにより、モデルはより多くのネガティブ サンプルから学習できるようになります。これは、2 つの最も代表的なメソッド SimCLR [2] と MoCo [3] のバッチ サイズにそれぞれ反映されています。メモリバンクのサイズ。ただし、ロングテール視覚認識タスクでは、カテゴリーの不均衡により、対照的なペアの数の増加によってもたらされる利得は、深刻な限界減少効果を生み出します。これは、対照的なペアのほとんどが頭部カテゴリーで構成されているためです。 . サンプルで構成されているため、テールカテゴリーをカバーするのは困難です。 たとえば、ロングテール Imagenet データセットで、バッチ サイズ (メモリ バンク) が共通の 4096 と 8192 に設定されている場合、各バッチ (メモリ バンク) には平均 212
と89 のカテゴリがあります。バンク) はそれぞれサンプル サイズが 1 未満です。 したがって、ProCo メソッドの中心的なアイデアは次のとおりです。ロングテール データセット上で、各タイプのデータの分布をモデル化し、パラメータを推定し、そこからサンプリングして対照的なペアを構築し、すべてのカテゴリが確実に覆われています。さらに、サンプル数が無限大になる傾向がある場合、対比損失の予想される解析解を理論的に厳密に導出できるため、それを最適化ターゲットとして直接使用して、対比ペアの非効率なサンプリングを回避し、無限数の対比を実現できます。比較学習。
しかし、上記のアイデアを実現するにはいくつかの主な困難があります: 各タイプのデータの分布をモデル化する方法。
- 分布のパラメーター、特にサンプル数が少ない末尾カテゴリーのパラメーターを効率的に推定する方法。
- コントラスト損失の期待される解析解が存在し、計算できることを確認する方法。
- 実際、上記の問題は統一確率モデルによって解決できます。つまり、特性分布をモデル化するためにシンプルで効果的な確率分布が選択され、最尤推定を使用してパラメータを効率的に推定できます。分布を計算し、対照的な損失に対する分析的な解決策を期待します。
対照学習の特徴は単位超球上に分布しているため、実現可能な解決策は、球上のフォン ミーゼス フィッシャー (vMF) 分布を特徴分布として選択することです (この分布は球上の正規分布に似ています) 。 vMF 分布パラメータの最尤推定には近似的な解析解があり、特徴量の一次モーメント統計のみに依存するため、分布パラメータを効率的に推定でき、コントラスト損失の期待値を厳密に導き出すことができます。無制限の数の対照的なペアの比較を実現します。
그림 1 ProCo 알고리즘은 다양한 배치의 특성을 기반으로 샘플 분포를 추정합니다. 무제한의 샘플을 샘플링함으로써 예상되는 대조 손실에 대한 분석 솔루션을 얻을 수 있으며 지도 대조 학습의 고유한 종속성을 효과적으로 제거할 수 있습니다. 배치 크기(메모리 뱅크) 크기.
방법 세부 사항
다음에서는 분포 가정, 매개변수 추정, 최적화 목표 및 이론적 분석의 네 가지 측면에서 ProCo 방법을 자세히 소개합니다.
분포 가정
앞서 언급했듯이 대조 학습의 기능은 단위 하이퍼스피어로 제한됩니다. 따라서 이러한 특징이 따르는 분포는 von Mises-Fisher(vMF) 분포라고 가정할 수 있으며 그 확률 밀도 함수는 다음과 같습니다. 
여기서 z는 p차원 특징의 단위 벡터이고 I는 수정된 제1종 베셀 함수
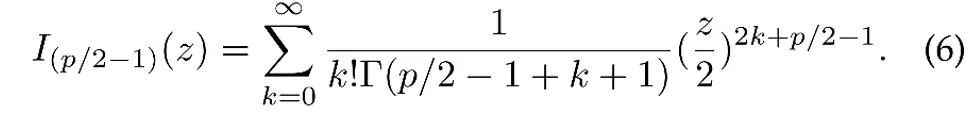
μ는 분포의 평균 방향이고, κ는 분포의 집중도를 제어하는 농도 모수입니다. κ가 더 클 경우 평균 근처에 샘플이 클러스터링되는 정도입니다. κ =0일 때 vMF 분포는 구형으로 변질됩니다.
매개변수 추정
위의 분포 가정을 기반으로 데이터 특징의 전체 분포는 혼합 vMF 분포이며, 여기서 각 범주는 vMF 분포에 해당합니다.

여기서 매개변수  는 훈련 세트의 카테고리 y의 빈도에 해당하는 각 카테고리의 사전 확률을 나타냅니다. 특징 분포의 평균 벡터
는 훈련 세트의 카테고리 y의 빈도에 해당하는 각 카테고리의 사전 확률을 나타냅니다. 특징 분포의 평균 벡터  및 집중 매개변수
및 집중 매개변수  는 최대 우도 추정을 통해 추정됩니다.
는 최대 우도 추정을 통해 추정됩니다.
N개의 독립 단위 벡터가 카테고리 y의 vMF 분포에서 샘플링되었다고 가정하면 평균 방향 및 농도 매개변수의 최대 우도 추정(대략)[4]은 다음 방정식을 만족합니다.
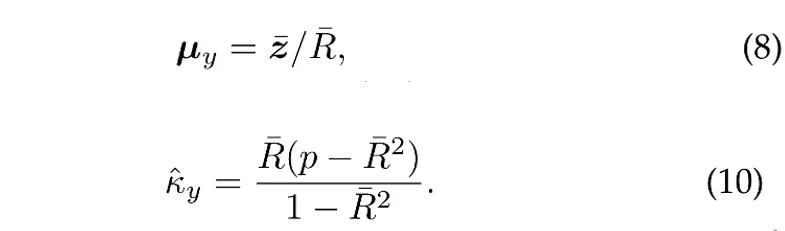
여기서  는 샘플입니다. 평균,
는 샘플입니다. 평균,  은 표본 평균의 계수 길이입니다. 또한, ProCo는 과거 표본을 활용하기 위해 꼬리 카테고리의 매개변수를 효과적으로 추정할 수 있는 온라인 추정 방법을 채택합니다.
은 표본 평균의 계수 길이입니다. 또한, ProCo는 과거 표본을 활용하기 위해 꼬리 카테고리의 매개변수를 효과적으로 추정할 수 있는 온라인 추정 방법을 채택합니다.
최적화 목표
추정된 매개변수를 기반으로 하는 간단한 접근 방식은 혼합 vMF 분포에서 샘플링하여 대조 쌍을 구성하는 것입니다. 그러나 각 훈련 반복에서 vMF 분포에서 많은 수의 샘플을 샘플링하는 것은 비효율적입니다. 따라서 본 연구에서는 이론적으로 샘플 수를 무한대로 확장하고, 예상 대비 손실 함수의 분석적 해를 엄격하게 도출하여 최적화 목표로 삼았다.

훈련 과정에서 추가 기능 분기(이 최적화 목표를 기반으로 한 표현 학습)를 도입함으로써 이 분기는 분류 분기와 함께 훈련될 수 있으며 추론 시 분류 분기만 필요하므로 증가하지 않습니다. 비용. 두 가지 손실의 가중합을 최종 최적화 목표로 사용하고 실험에서는 α=1로 설정합니다. 최종적으로 ProCo 알고리즘의 전체 과정은 다음과 같습니다. 이론적 분석
 ProCo 방법의 유효성을 이론적으로 검증하기 위해 연구진은 일반화 오류 한계와 초과 위험 한계를 분석했습니다. 분석을 단순화하기 위해 여기서는 y∈{-1,+1}이라는 두 가지 범주만 있다고 가정합니다. 분석 결과 일반화 오류 경계는 주로 훈련 샘플 수와 데이터 분산에 의해 제어되는 것으로 나타났습니다. 이 결과는 관련 연구[6][7]의 이론적 분석과 일치하여 ProCo 손실이 추가 요인을 도입하지 않고 일반화 오류 한계를 증가시키지 않는다는 것을 보장하며 이론적으로 이 방법의 효율성을 보장합니다.
ProCo 방법의 유효성을 이론적으로 검증하기 위해 연구진은 일반화 오류 한계와 초과 위험 한계를 분석했습니다. 분석을 단순화하기 위해 여기서는 y∈{-1,+1}이라는 두 가지 범주만 있다고 가정합니다. 분석 결과 일반화 오류 경계는 주로 훈련 샘플 수와 데이터 분산에 의해 제어되는 것으로 나타났습니다. 이 결과는 관련 연구[6][7]의 이론적 분석과 일치하여 ProCo 손실이 추가 요인을 도입하지 않고 일반화 오류 한계를 증가시키지 않는다는 것을 보장하며 이론적으로 이 방법의 효율성을 보장합니다.
또한 이 방법은 특성 분포 및 매개변수 추정에 대한 특정 가정에 의존합니다. 이러한 매개변수가 모델 성능에 미치는 영향을 평가하기 위해 연구진은 추정된 매개변수를 사용하여 예상되는 위험과 실제 분포에 있는 베이즈 최적 위험 사이의 편차를 측정하는 ProCo 손실의 초과 위험 한계도 분석했습니다. 매개변수.

이는 ProCo 손실의 초과 위험이 주로 매개변수 추정 오류의 1차 항에 의해 제어된다는 것을 보여줍니다.
실험 결과
핵심 동기를 검증하기 위해 연구자들은 먼저 다양한 배치 크기에서 다양한 대조 학습 방법의 성능을 비교했습니다. Baseline에는 롱테일 인식 작업에서 SCL을 기반으로 한 향상된 방법인 BCL(Balanced Contrastive Learning)이 포함되어 있습니다. 특정 실험 설정은 지도 학습(SCL)의 2단계 훈련 전략을 따릅니다. 즉, 먼저 표현 학습 훈련에 대비 손실만 사용한 다음 동결 백본을 사용하여 테스트하기 위해 선형 분류기를 훈련합니다.
아래 그림은 CIFAR100-LT(IF100) 데이터 세트에 대한 실험 결과를 보여줍니다. BCL 및 SupCon의 성능은 배치 크기에 따라 분명히 제한되지만 ProCo는 기능을 도입하여 SupCon이 배치 크기에 미치는 영향을 효과적으로 제거합니다. 각 카테고리의 의존성을 분산시켜 다양한 배치 크기에서 최고의 성능을 달성합니다.
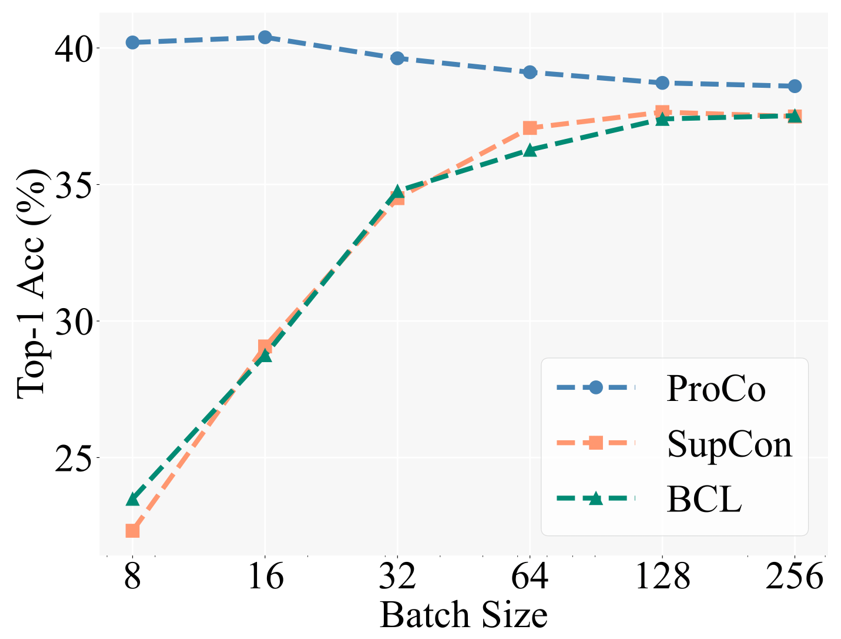
또한 연구원들은 롱테일 인식 작업, 롱테일 준지도 학습, 롱테일 객체 감지 및 균형 잡힌 데이터 세트에 대한 실험도 수행했습니다. 여기서는 주로 대규모 롱테일 데이터 세트 Imagenet-LT 및 iNaturalist2018에 대한 실험 결과를 보여줍니다. 첫째, 90세대의 훈련 일정에서 대조 학습을 개선하는 유사한 방법과 비교하여 ProCo는 두 개의 데이터 세트와 두 개의 백본에서 최소 1%의 성능 향상을 보였습니다.

다음 결과는 ProCo가 400 epoch 일정에서 더 긴 훈련 일정을 통해 이점을 얻을 수 있음을 추가로 보여줍니다. ProCo는 iNaturalist2018 데이터 세트에서 SOTA 성능을 달성했으며 다른 A가 아닌 조합과도 경쟁할 수 있음을 확인했습니다. 증류(NCL) 및 기타 방법을 포함한 대조 학습 방법. "시각적 표현의 대조 학습을 위한 간단한 프레임워크." PMLR에 관한 국제 회의, 2020.

- S . Sra, "von Mises-fisher 분포의 매개변수 근사에 대한 짧은 참고 사항: 및 is(x)의 빠른 구현", 계산 통계, 2012.
-
J. Zhu, et al. "긴 꼬리 시각적 인식을 위한 균형 잡힌 대조 학습", CVPR, 2022. - W. Jitkrittum, et al. "ELM: 긴 꼬리 학습을 위한 임베딩 및 로짓 마진," arXiv 사전 인쇄, 2022.
- A. K. Menon, et al. "로짓 조정을 통한 롱테일 학습", ICLR, 2021.
以上がTPAMI 2024 | ProCo: 無限対照ペアのロングテール対照学習の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

