ホームページ >バックエンド開発 >Python チュートリアル >K 最近傍回帰、回帰: 教師あり機械学習
K 最近傍回帰、回帰: 教師あり機械学習
- 王林オリジナル
- 2024-07-17 22:18:41978ブラウズ
k 最近傍回帰
k 最近傍 (k-NN) 回帰は、特徴空間内の k 近傍トレーニング データ ポイントの平均 (または加重平均) に基づいて出力値を予測するノンパラメトリック手法です。このアプローチでは、特定の関数形式を想定せずに、データ内の複雑な関係を効果的にモデル化できます。
k-NN 回帰法は次のように要約できます。
- 距離メトリック: アルゴリズムは距離メトリック (通常はユークリッド距離) を使用して、データ ポイントの「近さ」を判断します。
- k 近傍: パラメーター k は、予測を行うときに考慮する最近傍の数を指定します。
- 予測: 新しいデータ ポイントの予測値は、その k 個の最近傍の値の平均です。
主要な概念
非パラメトリック: パラメトリック モデルとは異なり、k-NN は入力特徴量とターゲット変数の間の基礎となる関係について特定の形式を想定しません。これにより、複雑なパターンを柔軟にキャプチャできるようになります。
距離計算: 距離メトリックの選択は、モデルのパフォーマンスに大きな影響を与える可能性があります。一般的なメトリックには、ユークリッド距離、マンハッタン距離、ミンコフスキー距離などがあります。
k の選択: 近傍数 (k) は相互検証に基づいて選択できます。 k が小さいと過学習につながる可能性があり、k が大きいと予測が平滑化されすぎて過小学習になる可能性があります。
k最近傍回帰の例
この例では、k-NN のノンパラメトリックな性質を利用しながら、多項式特徴を備えた k-NN 回帰を使用して複雑な関係をモデル化する方法を示します。
Python コード例
1.ライブラリをインポート
import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.preprocessing import PolynomialFeatures from sklearn.neighbors import KNeighborsRegressor from sklearn.metrics import mean_squared_error, r2_score
このブロックは、データ操作、プロット、機械学習に必要なライブラリをインポートします。
2.サンプルデータの生成
np.random.seed(42) # For reproducibility X = np.linspace(0, 10, 100).reshape(-1, 1) y = 3 * X.ravel() + np.sin(2 * X.ravel()) * 5 + np.random.normal(0, 1, 100)
このブロックは、いくつかのノイズとの関係を表すサンプル データを生成し、現実世界のデータの変動をシミュレートします。
3.データセットを分割します
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
このブロックは、モデル評価のためにデータセットをトレーニング セットとテスト セットに分割します。
4.多項式特徴の作成
degree = 3 # Change this value for different polynomial degrees poly = PolynomialFeatures(degree=degree) X_poly_train = poly.fit_transform(X_train) X_poly_test = poly.transform(X_test)
このブロックはトレーニング データセットとテスト データセットから多項式特徴を生成し、モデルが非線形関係をキャプチャできるようにします。
5. k-NN 回帰モデルの作成とトレーニング
k = 5 # Number of neighbors knn_model = KNeighborsRegressor(n_neighbors=k) knn_model.fit(X_poly_train, y_train)
このブロックは、k-NN 回帰モデルを初期化し、トレーニング データセットから導出された多項式特徴を使用してモデルをトレーニングします。
6.予測を立てる
y_pred = knn_model.predict(X_poly_test)
このブロックは、トレーニングされたモデルを使用してテスト セットで予測を行います。
7.結果をプロットする
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
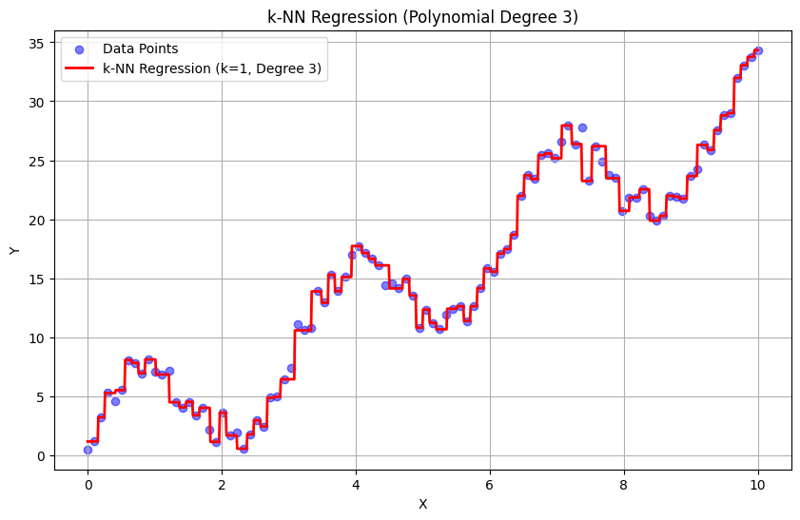
このブロックは、実際のデータ ポイントと k-NN 回帰モデルからの予測値の散布図を作成し、近似曲線を視覚化します。
k = 1 での出力:
k = 10 での出力:
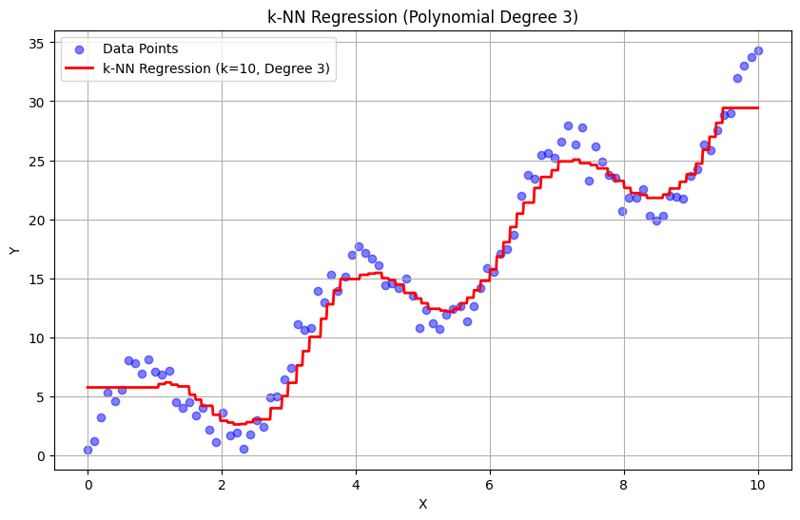
この構造化アプローチは、多項式特徴を使用した k 近傍回帰を実装して評価する方法を示します。 k-NN 回帰は、近隣の応答の平均化を通じてローカル パターンをキャプチャすることで、データ内の複雑な関係を効果的にモデル化し、簡単な実装を提供します。 k と多項式の次数の選択は、モデルのパフォーマンスと、根底にある傾向を捉える柔軟性に大きく影響します。
以上がK 最近傍回帰、回帰: 教師あり機械学習の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

