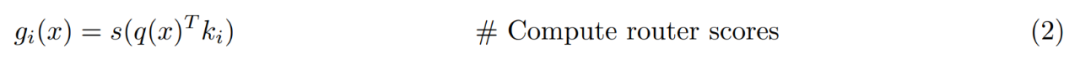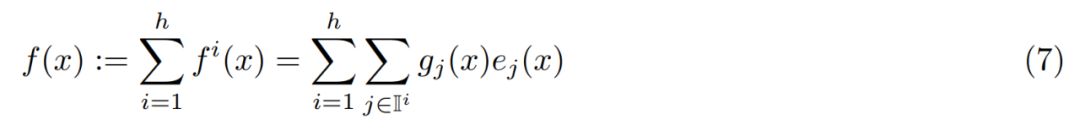計算効率を維持しながら、Transformer をさらに拡張する可能性を解き放ちます。標準の Transformer アーキテクチャの
フィードフォワード (FFW) 層では、隠れ層の幅が増加するにつれて、計算コストとアクティベーション メモリが直線的に増加します。大規模言語モデル (LLM) のサイズが増大し続けるにつれて、モデル サイズを計算コストから分離するスパース混合エキスパート (MoE) アーキテクチャがこの問題を解決する実現可能な方法になりました。多くの新しい MoE モデルは、同じサイズでより優れたパフォーマンスとより強力なパフォーマンスを実現できます。 最近発見された、きめの細かい MoE 拡張の法則は、より高い粒度がパフォーマンスの向上につながることを示しています。ただし、既存の MoE モデルは、計算と最適化の課題により、少数の専門家に限定されています。 今週火曜日、Google DeepMind の新しい研究では、プロダクト キー テクノロジーを活用して 100 万人のマイクロエキスパートからのスパース検索を実行する、パラメーター効率の良いエキスパート検索メカニズムが導入されています。 
リンク: https://arxiv.org/abs/2407.04153このアプローチは、学習されたインデックス構造を通じて多数の小さなエキスパートを効率的に連結することにより、パラメーター数から計算コストを切り離そうとします。ルーティング 。高密度 FFW、粗粒 MoE、プロダクト キー メモリ (PKM) レイヤーと比較して優れた効率を示します。 この作業では、プロダクト キーの取得を使用して多数のエキスパートに効率的にルーティングし、計算コストをパラメータの量から分離する、Parameter Efficient Expert Retrieval (PEER) アーキテクチャ (パラメータ効率的なエキスパート取得) を導入します。この設計は、実験で優れた計算パフォーマンス レベルを実証し、ベース モデルを拡張するための高密度 FFW レイヤーの競争力のある代替手段として位置付けられています。この研究の主な貢献は次のとおりです: 極端な環境省設定の調査: これまでの環境省研究では数人の大規模な専門家に焦点が当てられていたのとは異なり、この研究では多数の小規模な専門家の未解明な状況が調査されています。 ルーティングのための学習されたインデックス構造: 学習されたインデックス構造が 100 万人を超える専門家に効率的にルーティングできることを初めて実証しました。 新しいレイヤー設計: プロダクト キー ルーティングと単一ニューロン エキスパートを組み合わせて、大幅な計算オーバーヘッドを発生させずにレイヤー容量を拡張する PEER レイヤーを導入します。経験的な結果は、高密度 FFW、粗粒 MoE、およびプロダクト キー メモリ (PKM) レイヤーと比較して効率が高いことを示しています。 包括的なアブレーション研究: PEER のさまざまな設計選択 (エキスパートの数、アクティビティ パラメーター、ヘッドの数、クエリのバッチ正規化など) が言語モデリング タスクに及ぼす影響を研究します。 このセクションでは、研究者が、ルーティングでプロダクト キーを使用するハイブリッド エキスパート アーキテクチャであるパラメトリック効率的エキスパート検索 (PEER) レイヤーと単一ニューロン MLP を専門家。以下の図 2 は、PEER 層内の計算プロセスを示しています。 
ピアレイヤーの概要。正式には、PEER 層は関数 f : R^n → R^m であり、次の 3 つの部分で構成されます。N 個の専門家のプール E := {e_i}^N_i=1、ここで各専門家 e_i : R^n → R ^m は f と同じ署名を共有し、対応する N 個のプロダクト キー K := {k_i}^N_i=1 ⊂ R^d とクエリ ネットワーク q : R^n → R ^d をマッピングします。 x ∈ R^n をクエリ ベクトル q (x) に変換します。 T_k を上位 k の演算子 を表すものとします。入力 x が与えられると、最初に、対応するプロダクト キーがクエリ q (x) との内積が最も大きい k エキスパートのサブセットを取得します。 
次に、上位 k 人のエキスパートのクエリ キーの内積に非線形アクティベーション (ソフトマックスやシグモイドなど) を適用して、ルーティング スコアを取得します。 
最後に、ルーティングスコアによって重み付けされたエキスパートの出力を線形結合することによって出力が計算されます。 
プロダクト キーの取得。研究者は多数の専門家 (N ≥ 10^6) を利用するつもりであるため、式 1 の上位 k 個のインデックスを単純に計算するだけでは非常にコストがかかる可能性があるため、プロダクト キーの取得手法が適用されます。 N 個の独立した d 次元ベクトルをキー k_i として使用する代わりに、2 つの独立した d/2 次元サブキー セット (つまり、C、C ' ⊂ R d/2) からのベクトルを連結することによってそれらを作成します。効率的な専門家と複数のヘッドによる検索。他の MoE アーキテクチャとは異なり、これらのアーキテクチャは通常、各エキスパートの隠れ層を他の FFW 層と同じサイズに設定します。 PEER では、各エキスパート e_i はシングルトン MLP です。つまり、単一のニューロンを持つ隠れ層が 1 つだけあります:
研究者らは個々のエキスパートのサイズを変更しませんでしたが、使用されたマルチヘッド検索は次のとおりです。 PEER 層の表現能力を調整するために使用されます。これは、トランスフォーマーのマルチヘッド アテンション メカニズムや PKM のマルチヘッド メモリに似ています。 
具体的には、h 個の独立したクエリ ネットワークを使用し、各ネットワークが独自のクエリを計算し、k 個の専門家の別個のセットを取得します。ただし、異なるヘッドは同じプロダクト キーのセットを持つ同じエキスパート プールを共有します。これらの頭の出力は次のように簡単に要約されます:
?特定の MoE レイヤは、パラメータの総数 P、トークンごとのアクティブ パラメータの数 P_active、および単一エキスパートのサイズ P_expert の 3 つのハイパーパラメータによって特徴付けることができます。 Krajewski et al. (2024) は、MoE モデルのスケーリング則が次の形式であることを示しました:
PEER の場合、研究者は d_expert = 1 を設定することで可能な限り最小のエキスパート サイズを使用し、活性化されたニューロンの数は検索ヘッド この数値に、ヘッドごとに取得されるエキスパートの数を掛けます: d_active = hk。したがって、PEER の粒度は常に G = P_active/P_expert = d_active/d_expert = hk となります。 
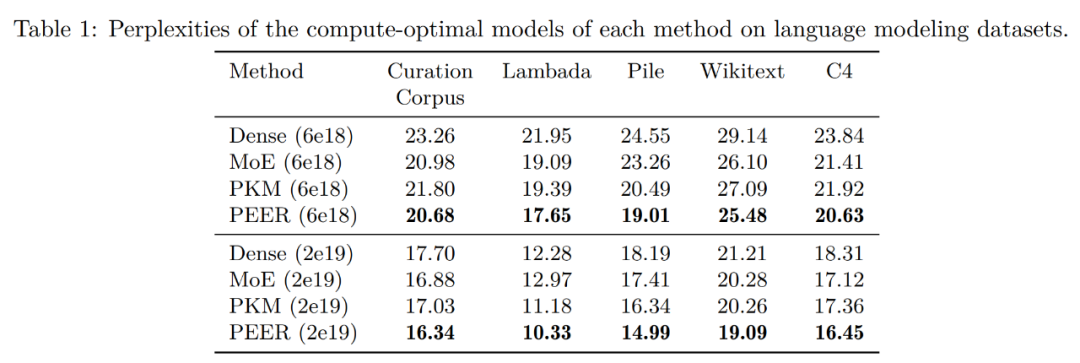
まず、言語モデリングデータセットの評価結果を見てみましょう。 isoFLOP 曲線に基づいて各手法の計算上最適なモデルを決定した後、研究者らは、次の一般的な言語モデリング データセットでこれらの事前トレーニングされたモデルのパフォーマンスを評価しました:
キュレーション コーパス
LambadaPileWikitext事前学習データセットC4
-
以下の表1に評価結果を示します。トレーニング中に使用された FLOP バジェットに基づいてモデルをグループ化しました。見てわかるように、これらの言語モデリング データセットでは、PEER の混乱度が最も低くなります。
アブレーション実験では、研究者は専門家の総数を変更しました。以下の図 1 の isoFLOP 曲線に示されているモデルにはすべて、100 万人 (1024^2) を超える専門家がいます。
研究者は、isoFLOP の最適な位置を持つモデルを選択し、アクティブなエキスパートの数を変更せずに、PEER 層のエキスパートの数 (N = 128^2、256^2、512^2、1024^2) を変更しました。 (h = 8、k = 16)。結果を以下の図 3(a) に示します。 isoFLOP 曲線は、中央ブロックの FFW 層を PEER 層に置き換えることなく、1024^2 のエキスパートを含む PEER モデルと対応する密なバックボーンの間を補間していることがわかります。これは、エキスパートの数を増やすだけでモデルのパフォーマンスを向上できることを示しています。 同時に、研究者らはアクティブな専門家の数を変更しました。彼らは、専門家の総数を一定(N = 1024^2)に保ちながら、アクティブな専門家の数を体系的に変化させました(hk = 32、64、128、256、512)。与えられた hk に対して、研究者は h と k を共同で変更して、最適な組み合わせを決定します。下の図 3 (b) は、ヘッド数 (h) に対する isoFLOP 曲線をプロットしています。
以下の表 2 は、BN を使用した場合と使用しない場合の、さまざまな数のエキスパートに対するエキスパートの使用量と不均一性を示しています。 1M エキスパートでもエキスパート利用率は 100% に近く、BN を使用することでエキスパート利用率のバランスが取れ、混乱レベルが低くなっていることがわかります。これらの調査結果は、多数の専門家を活用する際の PEER モデルの有効性を示しています。 
研究者らはまた、BN を使用した場合と使用しない場合の isoFLOP 曲線を比較しました。以下の図 4 は、BN を使用した PEER モデルが一般に低いパープレキシティを達成できることを示しています。違いは顕著ではありませんが、isoFLOP 最適領域付近で最も顕著です。 
PEER 研究の著者は Xu He (Owen) のみです。彼は Google DeepMind の研究科学者であり、オランダのフローニンゲン大学で博士号を取得しています。 2017年に。 
以上が単著論文、Google は密なフィードフォワードと疎な MoE を超える数百万の専門家の混合を提案の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
