ホームページ >Java >&#&チュートリアル >動的計画法を使用してフィボナッチ数を求める
動的計画法を使用してフィボナッチ数を求める
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBオリジナル
- 2024-07-17 00:12:31665ブラウズ
このセクションでは、動的計画法を使用してフィボナッチ数を見つけるための効率的なアルゴリズムを分析および設計します。セクション 18.3、ケーススタディ: フィボナッチ数の計算では、次のようなフィボナッチ数を見つけるための再帰的方法が説明されました:
/**フィボナッチ数を求める方法*/
public static long fib(long インデックス) {
if (index == 0) // 基本ケース
0 を返す;
else if (index == 1) // 基本ケース
1 を返します;
else // リダクションと再帰呼び出し
return fib(インデックス - 1) + fib(インデックス - 2);
}
これで、このアルゴリズムの複雑さは O(2^n) であることが証明できます。便宜上、インデックスを n とします。 T(n) が fib(n) を見つけるアルゴリズムの複雑さを表し、c が 0 および 1 とインデックスを比較するための定数時間を表すものとします。つまり、T(1) と T(0) は c です。したがって、

ハノイ塔問題の分析と同様に、T(n) が O(2^n) であることを示すことができます。
ただし、このアルゴリズムは効率的ではありません。フィボナッチ数を見つけるための効率的なアルゴリズムはありますか?再帰的 fib メソッドの問題点は、メソッドが同じ引数で重複して呼び出されることです。たとえば、fib(4) を計算するには、fib(3) と fib(2) が呼び出されます。 fib(3) を計算するには、fib(2) と fib(1) が呼び出されます。 fib(2) が冗長に呼び出されることに注意してください。同じ引数を使用して fib メソッドを繰り返し呼び出さないようにすることで、この問題を改善できます。新しいフィボナッチ数は、シーケンス内の前の 2 つの数値を加算することによって取得されることに注意してください。 2 つの変数 f0 と f1 を使用して前の 2 つの数値を保存すると、f0 を追加することで新しい数値 f2 をすぐに取得できます。 と f1。 f1 を f0 に割り当て、f2 を f1 に割り当てることで、f0 と f1 を更新する必要があります。 、以下の図に示すように。

新しいメソッドは以下のコードに実装されています。
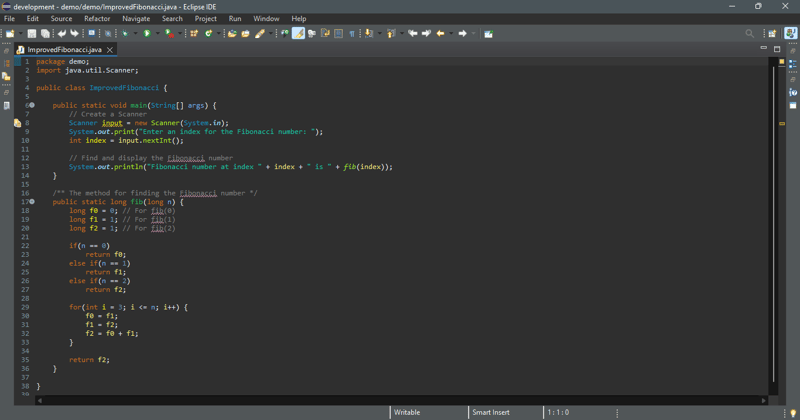
フィボナッチ数のインデックスを入力します: 6
インデックス 6 のフィボナッチ数は 8
フィボナッチ数のインデックスを入力します: 7
インデックス 7 のフィボナッチ数は 13
明らかに、この新しいアルゴリズムの複雑さは O(n) です。これは、再帰的 O(2^n) アルゴリズムに比べて大幅な改善です。
ここで紹介するフィボナッチ数を計算するアルゴリズムは、動的計画法として知られるアプローチを使用します。動的プログラミングは、部分問題を解決し、次に部分問題の解を組み合わせて全体の解を得るプロセスです。これは当然、再帰的な解決策につながります。ただし、部分問題が重複するため、再帰を使用するのは非効率的です。動的プログラミングの背後にある重要な考え方は、部分問題の冗長な計算を避けるために、各部分問題を 1 回だけ解決し、後で使用できるように部分問題の結果を保存することです。
以上が動的計画法を使用してフィボナッチ数を求めるの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

