ホームページ >Java >&#&チュートリアル >ケーススタディ: 階乗の計算
ケーススタディ: 階乗の計算
- 王林オリジナル
- 2024-07-16 07:11:191010ブラウズ
再帰的メソッドは、それ自体を呼び出すメソッドです。多くの数学関数は再帰を使用して定義されます。簡単な例から始めましょう。数値 n の階乗は、次のように再帰的に定義できます:
0! = 1;
ん! = n × (n - 1)!; n > 0
指定された n に対して n! をどのように見つけますか? 1! を見つけるのは簡単です。0! は 1 であり、1! は 1 × 0 であることがわかっているからです。 !。 (n - 1)! がわかっているとすると、n × (n - 1)! を使用すると、すぐに n! を求めることができます。したがって、n! を計算する問題は、(n - 1)! を計算することに帰着します。 (n - 1)! を計算するとき、n が 0 になるまで同じアイデアを再帰的に適用できます。
factorial(n) を n! を計算するメソッドとします。 n = 0 を指定してメソッドを呼び出すと、すぐに結果が返されます。このメソッドは、基本ケースまたは停止条件と呼ばれる最も単純なケースを解決する方法を知っています。 n > を指定してメソッドを呼び出すと、 0 の場合、問題を n - 1 の階乗を計算するための部分問題に縮小します。 部分問題は、元の問題と本質的に同じですが、より単純であるか、小さくなっています。副問題には元の問題と同じプロパティがあるため、別の引数を使用してメソッドを呼び出すことができます。これは再帰呼び出しと呼ばれます。
factorial(n) を計算するための再帰アルゴリズムは、次のように簡単に説明できます。
if (n == 0)
1 を返します;
それ以外
n * 階乗(n - 1)を返す;
メソッドは部分問題を新しい部分問題に分割し続けるため、再帰呼び出しではさらに多くの再帰呼び出しが行われる可能性があります。再帰的メソッドを終了するには、問題を最終的に停止ケースに絞り込む必要があり、その時点でメソッドは呼び出し元に結果を返します。次に、呼び出し元は計算を実行し、その結果を自身の呼び出し元に返します。このプロセスは、結果が元の呼び出し元に返されるまで続きます。元の問題は、factorial(n - 1) の結果を n に乗算することで解決できます。
以下のコードは、ユーザーに非負の整数の入力を求め、その数値の階乗を表示する完全なプログラムを提供します。

factorial メソッド (17 ~ 22 行目) は、本質的には、階乗の再帰数学的定義を Java コードに直接変換したものです。 factorial への呼び出しは、それ自体を呼び出すため再帰的です。 factorial に渡されるパラメーターは、基本ケースの 0 に達するまで減分されます。
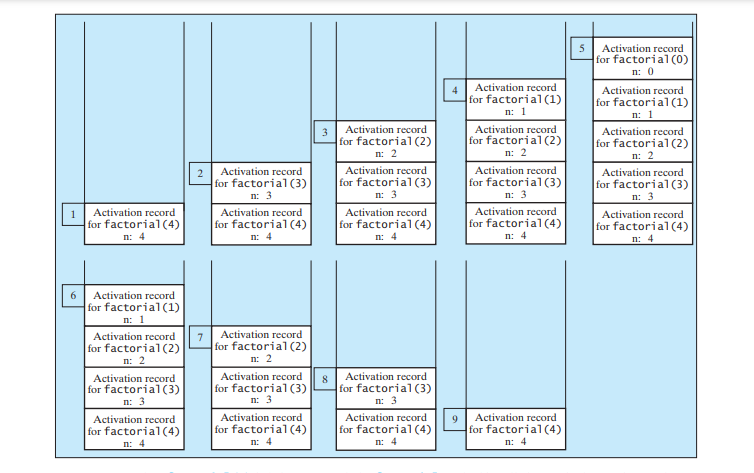
再帰メソッドの書き方がわかりました。再帰はバックグラウンドでどのように機能するのでしょうか?以下の図は、n = 4.
から始まる再帰呼び出しの実行を示しています。
再帰呼び出しでのスタック領域の使用を下の図に示します。
ループを使用して 階乗 メソッドを実装する方が簡単で効率的です。ただし、ここでは再帰の概念を示すために再帰的 階乗 メソッドを使用します。この章の後半では、本質的に再帰的であり、再帰を使用しないと解決するのが難しいいくつかの問題を紹介します。
最終的に基本ケースに収束するような方法で再帰によって問題が軽減されない場合、または基本ケースが指定されていない場合、無限再帰が発生する可能性があります。たとえば、誤って factorial メソッドを次のように書いたとします。
パブリック 静的ロング階乗 (int n) {
n * 階乗(n - 1)を返す;
}
メソッドが無限に実行され、StackOverflowError が発生します。
このセクションで説明する例は、それ自体を呼び出す再帰メソッドを示しています。これは直接再帰として知られています。 間接再帰を作成することも可能です。これは、メソッド A がメソッド B を呼び出し、メソッド B がメソッド A を呼び出すときに発生します。再帰にはさらにいくつかのメソッドが関与する可能性もあります。たとえば、メソッド A はメソッド B を呼び出し、このメソッド C がメソッド
A を呼び出します。以上がケーススタディ: 階乗の計算の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

