ホームページ >テクノロジー周辺機器 >AI >そこに集中してください! !因果推論のための 2 つの主要なアルゴリズム フレームワークの分析
そこに集中してください! !因果推論のための 2 つの主要なアルゴリズム フレームワークの分析
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBオリジナル
- 2024-06-04 16:45:02791ブラウズ
1. 全体的なフレームワーク

主なタスクは 3 つのカテゴリに分類できます。 1 つ目は因果構造の発見、つまりデータから変数間の因果関係を特定することです。 2 つ目は因果効果の推定です。つまり、ある変数が別の変数に及ぼす影響の程度をデータから推測します。この影響は相対的な性質を指すのではなく、1 つの変数が介入したときに別の変数の値または分布がどのように変化するかを指すことに注意してください。最後のステップはバイアスを修正することです。多くのタスクでは、さまざまな要因によって開発サンプルとアプリケーション サンプルの配布が異なる可能性があるためです。この場合、因果推論はバイアスを修正するのに役立つ可能性があります。
これらの関数はさまざまなシナリオに適していますが、最も典型的なのは意思決定シナリオです。因果推論を通じて、さまざまなユーザーが私たちの意思決定行動にどのように反応するかを理解できます。第 2 に、産業シナリオでは、ビジネス プロセスが複雑で長いことが多く、データの偏りにつながります。因果推論を通じてこれらの逸脱の因果関係を明確に記述することは、逸脱を修正するのに役立ちます。さらに、多くのシナリオでは、モデルの堅牢性と解釈可能性に対して高い要件が課されます。このモデルが因果関係に基づいて予測を行うことができ、因果推論がより強力な説明モデルの構築に役立つことが期待されています。最後に、意思決定の結果の影響を評価することも重要です。因果推論は、戦略の実際の効果をより適切に分析するのに役立ちます。
次に、因果推論において重要な2つの問題、すなわち、シーンが因果推論に適しているかどうかを判断する方法と、因果推論における代表的なアルゴリズムを紹介します。 まず、シナリオが因果推論の適用に適しているかどうかを判断することが重要です。因果推論は通常、因果関係の問題を解決するために、つまり、観察されたデータを通じて原因と結果の関係を推測するために使用されます。したがって、
を判断する場合 2. アプリケーションシナリオの評価(意思決定問題)
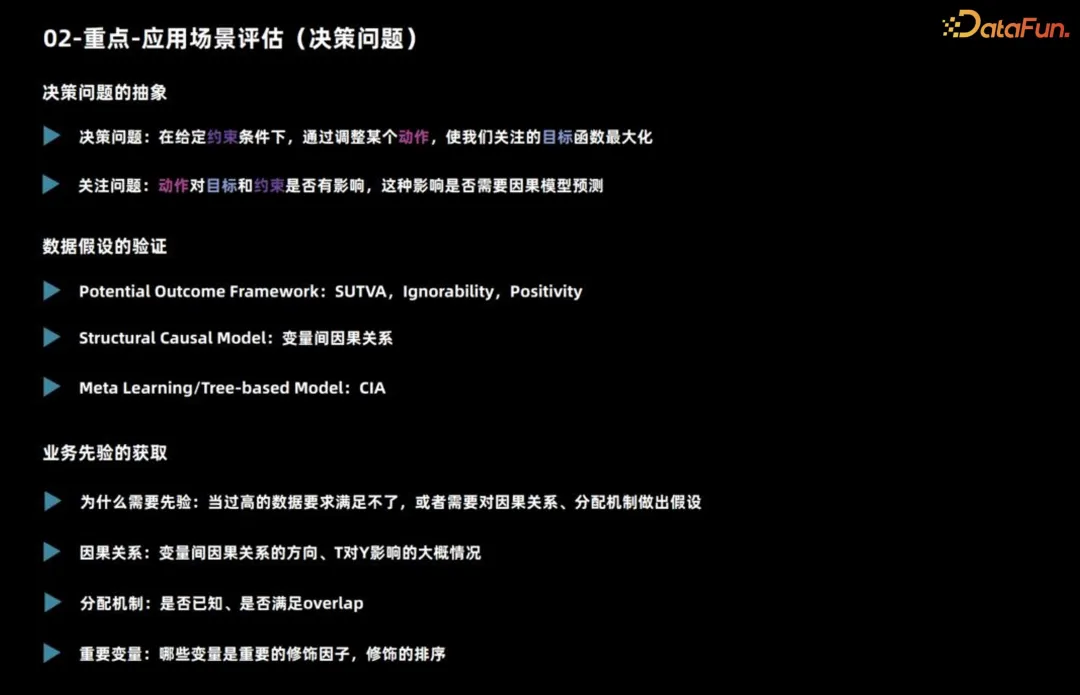
まず、シナリオが推論を使用するのに適しているかどうかを判断することを紹介します。主に意思決定の問題が含まれます。
意思決定の問題については、まずそれが何であるか、つまり、どの目標を最大化するためにどのような制約の下でどのような行動をとるべきかを明確にする必要があります。次に、このアクションが目標と制約に影響を与えるかどうか、予測に因果推論モデルを使用する必要があるかどうかを検討する必要があります。 たとえば、製品をマーケティングする場合、通常、総予算を考慮して、各ユーザーにクーポンを発行するか、割引を発行するかを検討します。全体的な目標として売上を最大化することを検討してください。予算の制約がない場合、最終的な売上に影響する可能性がありますが、前向きな戦略であることを理解している限り、すべてのユーザーに割引を与えることができます。 この場合、意思決定アクションはターゲットに影響を与えますが、予測に因果推論モデルを使用する必要はありません。
以上が意思決定問題の基本的な分析であり、さらにデータ項目が満たされているかどうかを観察する必要があります。因果モデルを構築する場合、因果アルゴリズムが異なれば、データとタスクの仮定に対する要件も異なります。
- 潜在的な結果クラスのモデルには 3 つの重要な前提があります。まず、個々の因果効果が安定している必要があります。たとえば、クーポン発行がユーザーの購入確率に及ぼす影響を調査する場合、ユーザーの行動がオフラインでの価格比較や影響を受けるなど、他のユーザーの影響を受けないようにする必要があります。さまざまな割引効果のあるクーポンによって。 2 番目の仮定は、ユーザーの実際の処理と潜在的な結果は、特有の状況を考慮すると独立しており、観察されていない交絡に対処するために使用できるということです。 3 番目の仮説は重複に関するものです。つまり、どの種類のユーザーも異なる決定を下す必要があり、そうでなければ、異なる決定の下でのこの種類のユーザーのパフォーマンスは観察できません。
- 構造因果モデルが直面する主な仮定は変数間の因果関係であり、これらの仮定を証明するのは多くの場合困難です。メタ学習とツリーベースの手法を使用する場合、通常は条件付きの独立性が前提となります。つまり、与えられた特徴、意思決定アクション、および潜在的な結果は独立しています。この仮定は、前述の独立性の仮定と似ています。
実際のビジネスシーンでは、事前知識を理解することが重要です。まず、これまでの判断の根拠となる実際の観測データの分布メカニズムを理解する必要があります。最も正確なデータが利用できない場合、推測を行うために仮定に頼る必要がある場合があります。第 2 に、ビジネス経験は、特徴量エンジニアリングにとって重要な因果効果の区別にどの変数が大きな影響を与えるかを判断する際に役立ちます。したがって、実際のビジネスに取り組む際、観測データやビジネス経験の流通メカニズムと組み合わせることで、課題に適切に対処し、意思決定や特徴量エンジニアリングを効果的に実行できるようになります。
3. 典型的な因果アルゴリズム

2 番目の重要な問題は、因果推論アルゴリズムの選択です。
1つ目は、因果構造発見アルゴリズムです。これらのアルゴリズムの中心的な目的は、変数間の因果関係を判断することです。主な研究アイデアは 3 つのカテゴリーに分類できます。 1つ目は、因果関係グラフにおけるノードネットワークの条件独立特性に基づいて判定する方法である。もう 1 つのアプローチは、因果関係図の品質を測定するスコアリング関数を定義することです。例えば、尤度関数を定義することにより、その関数を最大化する有向非巡回グラフを探索し、因果グラフとして使用する。 3 番目のタイプの方法では、より多くの情報が導入されます。たとえば、2 つの変数の実際のデータ生成プロセスが n m タイプ (加法性ノイズ モデル) に従っていると仮定し、2 つの変数間の因果関係の方向を解きます。
因果効果の推定には、さまざまなアルゴリズムが含まれます。以下に、一般的なアルゴリズムをいくつか示します。
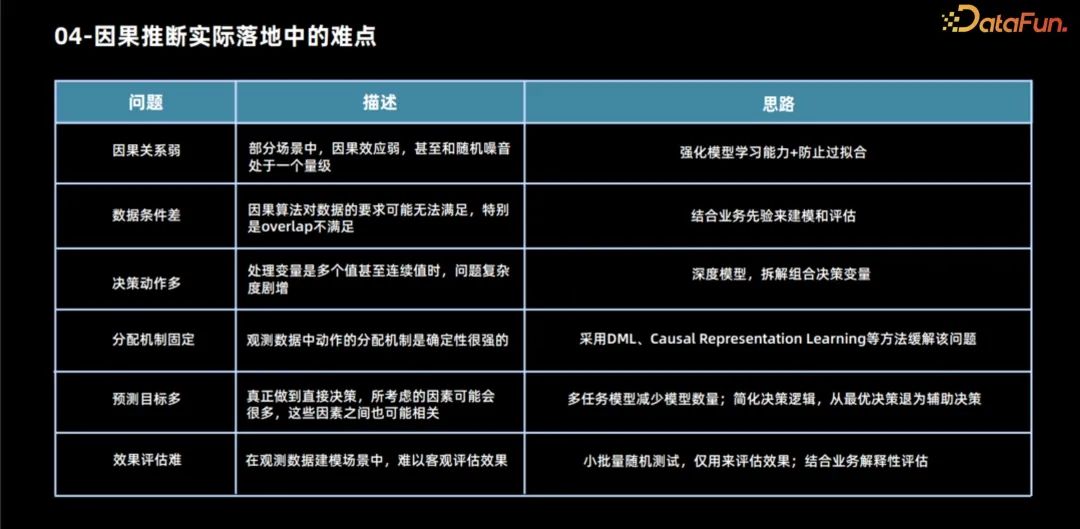
因果推論は、実際の応用において多くの課題に直面します。
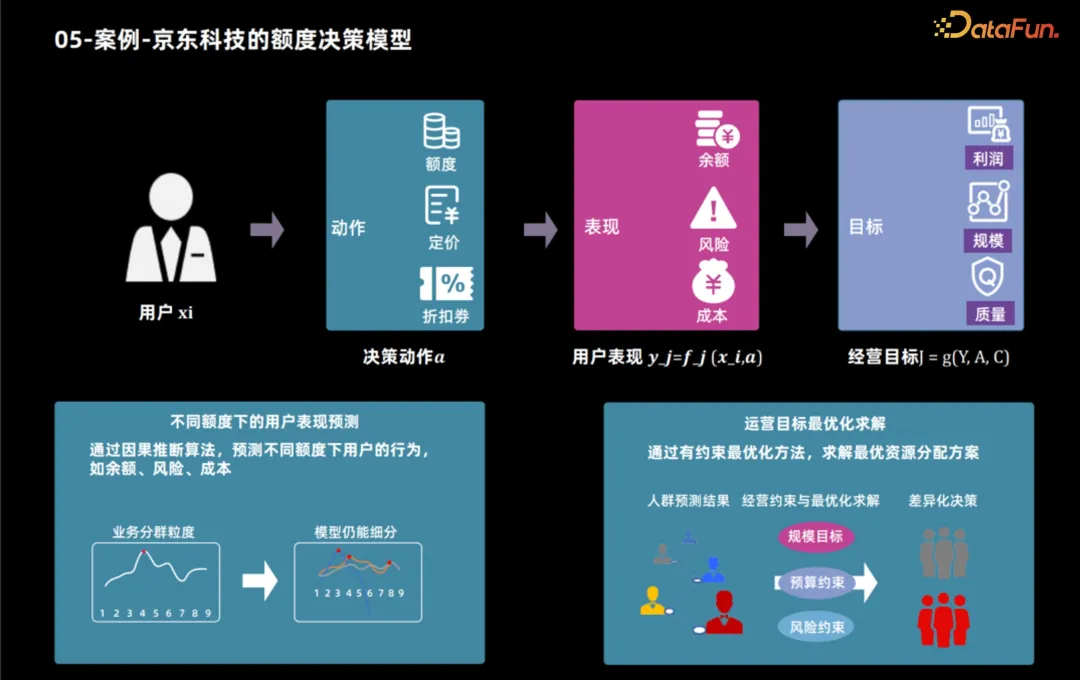
次に、因果推論技術を使用してクレジット商品を策定するための JD Technology の補助アプリケーションを取り上げます。例として、因果推論テクノロジーを使用してクレジット商品を策定する方法を示します。ビジネス目標が決定されると、通常、これらの目標はユーザーの製品使用状況や借入行動などのユーザー パフォーマンス指標に分類できます。これらの指標を分析することで、利益や規模などの経営目標を算出することができます。したがって、与信限度額の決定プロセスは 2 つのステップに分かれています。まず、因果推論テクノロジーを使用して、さまざまな与信限度額の下でユーザーのパフォーマンスを予測し、次にさまざまな方法を使用して、これらのパフォーマンスに基づいて各ユーザーに最適な与信限度額を決定します。運用目標。
私たちは将来の発展において、一連の課題と機会に直面します。 まず第一に、現在の因果モデルの欠点を考慮して、学界は一般に、より複雑な非線形関係を処理するには大規模なモデルが必要であると考えています。因果モデルは通常 2 次元データのみを扱い、ほとんどのモデル構造は比較的単純であるため、将来の研究の方向性にはこの問題への対処が含まれる可能性があります。 第二に、研究者らは因果表現学習の概念を提案し、表現学習における切り離しとモジュール化されたアイデアの重要性を強調しました。データ生成プロセスを因果関係の観点から理解することで、現実世界の法則に基づいて構築されたモデルの転送機能と一般化が向上する可能性があります。 最後に、研究者らは、現在の仮定が強すぎて多くの場合実際のニーズを満たすことができないため、シナリオごとに異なるモデルを採用する必要があると指摘しました。これにより、モデル実装のしきい値が非常に高くなります。したがって、汎用性の高いスネークオイルアルゴリズムを見つけることは非常に価値があります。
4. 因果推論の実際の実装における困難さ
5. ケース - JD Technology の信用限度額決定モデル
6. 将来の発展

以上がそこに集中してください! !因果推論のための 2 つの主要なアルゴリズム フレームワークの分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

