Meta FAIR はハーバード大学と連携して、大規模な機械学習によって引き起こされるデータの偏りを最適化するための新しい研究フレームワークを提供しました。
ご存知のとおり、大規模な言語モデルのトレーニングには数か月かかることが多く、数百、さらには数千の GPU が使用されます。 LLaMA2 70B モデルを例にとると、そのトレーニングには合計 1,720,320 GPU 時間が必要です。大規模なモデルのトレーニングには、これらのワークロードの規模と複雑さにより、特有のシステム上の課題が生じます。
最近、多くの機関が、SOTA 生成 AI モデルをトレーニングする際のトレーニング プロセス中の不安定性を報告しています。これらは通常、Google の PaLM モデルなど、トレーニング プロセス中に最大 20 回発生する損失スパイクの形で発生します。スパイク。
このトレーニングの不正確さの根本原因は数値の偏差です。大規模な言語モデルのトレーニングの実行コストは非常に高いため、数値の偏差をどのように定量化するかが重要な問題となっています。
最新の研究では、メタ大学とハーバード大学の研究者が、トレーニング最適化における数値バイアスを理解するための原理に基づいた定量的手法を開発しました。これは、さまざまな最先端の最適化手法を評価し、大規模なモデルのトレーニングに使用した場合に予期しない不安定性が生じる可能性があるかどうかを判断するために使用されます。 研究者らは、既存の最適化手法は一部のタスクではうまく機能するものの、大規模なモデルに適用すると数値的な偏差が発生することを発見しました。この数値的な偏りにより、トレーニング プロセス中に不安定性が生じ、モデルのパフォーマンスが低下する可能性があります。 この問題を解決するために、研究者らは原理に基づいた定量的手法に基づく最適化を提案しました

- 論文のタイトル: フラッシュアテンションは安定していますか?
- 論文リンク: https://arxiv.org/pdf/2405.02803
単一の前方パスでは、フラッシュ アテンションの数値偏差が BF16 のベースライン アテンションよりも一桁大きいことがわかりました。
具体的には、この方法は次の 2 つの段階で構成されます:
- 特定の最適化における数値精度を変動させるマイクロベンチマークを開発する
- データ駆動型分析を通じて数値を評価するWasserstein 距離に基づくバイアスがモデルの重みの変化にどのように変換されるか。
研究者らは SOTA 最適化技術 Flash Attend を分析し、導入される可能性のある数値偏差を定量化しました。フラッシュ アテンションは、アテンション メカニズムを加速するために広く使用されているテクノロジーであり、Transformer モデルではシステムのボトルネックとみなされることがよくあります。 Flash アテンションは速度を向上させ、メモリ アクセスを削減しますが、アルゴリズムの最適化にも依存しており、アルゴリズムの最適化により数値の偏差が増加する可能性があります。
研究者らは、リスケーリング係数を追加すると意図しない近似が生じ、数値的なトレードオフが生じ、その後トレーニングの安定性に影響を与える可能性があると仮説を立てました。
彼らは、マルチモーダルなテキストから画像へのワークロードのコンテキストで Flash アテンションを分析し、Flash アテンションとそのベースラインの間の数値偏差の潜在的な重要性を判断しました。最終的に、彼らはトレーニング最適化の数値バイアスとその下流効果を定量化するフレームワークを導入しました。
研究者は、数値偏差の定量化において次の 2 つの主な貢献を行いました:
(1) 数値偏差に対する数値精度の影響を分離するマイクロベンチマークを設計しました。
研究者によって設計されたマイクロベンチマークは、従来のブラックボックス最適化 (フラッシュ アテンションなど) によって引き起こされる数値偏差を測定および定量化するために使用される手法です。彼らは、提供されたカーネルでは通常利用できない側面を混乱させることにより、低い数値精度 (BF16) では、フラッシュ アテンションがベースライン アテンションと比較して約 1 桁高い数値バイアスを持つことを発見しました。
(2) Wasserstein Distance メトリクスに基づいてデータ駆動型分析を実行しました。
この分析を通じて、研究者は観察された数値偏差を文脈化し、下流モデルのプロパティへの影響の上限を形成します。研究者のケーススタディでは、観察された数値バイアスの影響を制限することができ、「Flash Attendance では、低精度トレーニング の約 1/2 ~ 1/5 倍のモデル重みバイアスが導入された」ことがわかりました。
この研究は、「数値バイアスに対するトレーニング最適化の影響を定量化するだけでなく、その影響を文脈化する」ための原則に基づいたアプローチを開発することの重要性を強調しています。プロキシを構築して数値バイアスの文脈を文脈化し、下流のモデル効果の可能性を推測することを目的としています。 、トレーニングの不安定さなど)、測定するのが難しいことがよくあります。
実験方法
研究者らはまず、フラッシュアテンションによって引き起こされる数値偏差を分離して研究するためのマイクロベンチマークを開発しました。図 2 に示すように、彼らは Flash アテンションを数値的に再実装して、さまざまな数値精度を分析し、アルゴリズムの各ステップで潜在的な最適化措置を適用しました。

図 2: マイクロベンチマーク設計の概要。
Flash アテンション コアは現在 FP16 および BF16 数値形式のみをサポートしているため、これが必要です。このカーネルは CUDA コードのラッパー API 呼び出しでもあるため、数値バイアスの影響を調べるためにアルゴリズムを混乱させることが困難になります。
対照的に、マイクロベンチマーク設計では、アルゴリズム内での正確な入力と変更が可能です。研究者らは、オリジナルの Flash アテンション カーネルに対してマイクロベンチマークを検証しました。
彼らはさらに、モデル実行中の各ステップでアテンション マトリックスの出力を比較する手法を設計しました。また、アテンションが呼び出されるたびにベースライン アテンションとフラッシュ アテンションを計算するようにモデル コードを変更しました。これにより、同じ入力行列に対する正確な出力行列の比較が可能になります。
これを状況に合わせて説明するために、最大差分メトリクスと Wasserstein Distance メトリクスを使用して、同一の独立したトレーニング実行を使用したトレーニング全体でのモデルの重みの差を定量化しました。
トレーニング実験では、研究者らはテキスト入力を画像に変換する生成 AI ワークロード (つまり、テキストから画像へのモデル) を使用しました。彼らは Shutterstock データセットを使用してモデルを再トレーニングし、NVIDIA 80GB A100 GPU のクラスターで実験を実行しました。
マイクロベンチマークによる数値偏差の定量化
研究者らはまず、フォワードパスプロセスにおけるフラッシュアテンションの影響を分析しました。彼らはマイクロベンチマークを使用して、ランダムに初期化されたクエリ、キー、および値のベクトルが同じであるという条件下で、アテンションによって計算された出力行列に対するさまざまな数値精度の影響を調べました。
図 3 に示すように、研究者が BF16 から FP64 までのさまざまな数値形式を使用すると、仮数部の桁数が増加するにつれて、フラッシュ アテンションとベースライン アテンションの間の数値偏差が減少します。これは、数値の違いが仮数部の桁が少ないことに固有の近似によるものであることを示唆しています。

図 3: フラッシュ アテンションの数値偏差に対する数値形式の影響。
その後、研究者は、標準的な比較のために FP64 数値形式でベースライン注意力の「ゴールデン値」を設定し、さまざまな数値形式での注意力出力をこの値と比較しました (図 4 を参照)。

図 4: FP64 におけるベースライン アテンション「ゴールド値」の比較。
結果は、BF16 では Flash Attendance の数値偏差が Baseline の数値偏差の約 10 倍であることを示しています。
この観測された数値偏差をさらに分析するために、研究者らはタイル サイズと SRAM サイズを一定に保ちながら行列のシーケンス長をスキャンしました (図 5 を参照)。

図 5: フラッシュ アテンションの数値偏差に対するシーケンスの長さの影響。
図に示すように、シーケンスの長さが増加するにつれて、(a) 最大差の上限、または (b) 差の平均および標準偏差によって測定されるかどうかにかかわらず、フラッシュ アテンションとベースラインの差は注意 数値の偏差が増加しています。
さらに、研究者は、数値偏差の影響をより深く理解するために、マイクロベンチマーク設計を使用してさまざまな最適化を行った実験も行っています (図 6 を参照)。
図 6a は、ブロック次元の順序を入れ替えることにより、フラッシュ アテンションとベースライン アテンションの間の数値の差がどのように増加するかを示しています。タイル サイズを正方形に制限するなど、図 6b の他の摂動は数値バイアスに影響を与えません。図 6c は、ブロック/タイル サイズが大きくなるほど、数値偏差が小さくなることを示しています。

図 6: アルゴリズムの変更と、観測された数値偏差に対するその影響。
重みの違いによる数値バイアスを理解する
フラッシュ アテンションはフォワード パス中にアテンション出力に数値バイアスを引き起こす可能性がありますが、この研究の最終目標は、モデル トレーニング中にこれが発生するかどうかを判断し、影響を調査することです。それはトレーニングの不安定さにつながります。
したがって、研究者らは、フラッシュ アテンションがトレーニング中にモデルを変更するかどうか、つまり、上記で観察されたアテンション出力の違いがトレーニング中に更新されたモデルの重みに反映されるかどうかを定量化したいと考えています。
研究者らは 2 つの指標を使用して、ベースライン アテンションを使用してトレーニングされたモデルとフラッシュ アテンションを使用してトレーニングされたモデル間のモデルの重みの違いを測定しました。まず最大差が計算されます。つまり、重み行列間の差の絶対値を見つけて最大値を取得し、次のように偏差の上限を取得します。数値偏差の上限ですが、各行列の分布は考慮されていません。したがって、研究者は、テンソル間の類似性の一般的な尺度である Wasserstein Distance を通じて重みの違いを定量化します。計算的には若干複雑ですが、Wasserstein Distance には、類似性を測定するためのテンソル分布の形状情報が含まれています。計算式は次のように要約されます。

値が小さいほど、行列間の類似性が高くなります。
 これら 2 つの指標を使用して、研究者らは、トレーニング プロセス全体を通じて、フラッシュ アテンションのモデルの重みがベースライン アテンションと比較してどのように変化したかを定量化しました。トレーニング プロセス全体で、フラッシュ アテンションを追加するとモデルの重みが変化します。トレーニングが継続するにつれて、この差はますます大きくなるだけです。これは、フラッシュ アテンションを使用してトレーニングされたモデルが、ベースライン アテンションを使用してトレーニングされたモデルとは異なることを示しています。トレーニングされた同じモデルが別のモデルに収束しました。
これら 2 つの指標を使用して、研究者らは、トレーニング プロセス全体を通じて、フラッシュ アテンションのモデルの重みがベースライン アテンションと比較してどのように変化したかを定量化しました。トレーニング プロセス全体で、フラッシュ アテンションを追加するとモデルの重みが変化します。トレーニングが継続するにつれて、この差はますます大きくなるだけです。これは、フラッシュ アテンションを使用してトレーニングされたモデルが、ベースライン アテンションを使用してトレーニングされたモデルとは異なることを示しています。トレーニングされた同じモデルが別のモデルに収束しました。
ただし、トレーニングは確率的プロセスであり、モデル構造の特定の変更により、下流の効果と精度の点で同様の結果が生じる可能性があります。これは、フラッシュ アテンションとベースライン アテンションでトレーニングされたモデルの重みが異なる場合でも注目に値します。
モデルを完全にトレーニングして精度を評価することは、特にトレーニングに数か月かかる大規模なモデルの場合、コストがかかり、リソースを大量に消費するタスクです。

(a) これらの重みの変更の重要性は何ですか?
(b) これは、他の広く採用されているトレーニング最適化における標準重量の変更に関連している可能性がありますか?
この目標を達成するために、研究者たちは、さまざまなシナリオの下でトレーニングプロセス中に体重の差がどのように変化するかを比較する一連の実験を設計しました。
フラッシュ アテンションとベースライン アテンションを使用したトレーニング プロセスの比較に加えて、トレーニングの開始時に重みが異なるランダム値に初期化された同じトレーニング プロセス中の重みの違いも定量化しました。ランダムな重みの初期化は一般的な手法であり、多くの場合同等の結果が生成されるため、これにより制限が提供されます。
さらに、研究者たちは、さまざまな精度でトレーニングされたモデルの重みの変化も測定しました。数値精度 (つまり、FP16 対 FP32) は下流の変更を引き起こす可能性があり、これはフラッシュ アテンションの重みの重要性の上限として機能します。 図 8 に示すように、フラッシュ アテンションを使用したモデルの重みバイアス変化率は、さまざまなモデル初期化の重みバイアス変化率と同等か、それより小さいことがわかります (赤と青の曲線の傾きに注目してください)。 。 また、FP16を使用した場合とFP32を使用した場合の重量変化率は高く、異なるモデルを初期化した場合よりも変化が大きくなります。 これらの結果はプロキシを提供し、次のことを示しています: 「フラッシュ アテンションは数値的なバイアスを示しますが、ランダムなモデルの初期化と低精度のトレーニングによって制限されます。また、低精度でトレーニングする場合、導入されるモデルの重みバイアスは約 10% です」 1/2 ~ 1/5 回。「 」 図 8: Wasserstein Distance メトリックを使用して測定されたトレーニング中の相対的な体重差。 研究の詳細については、元の論文を参照してください。 
以上がフラッシュ アテンションは安定していますか?メタとハーバードは、モデルの重みの偏差が桁違いに変動していることを発見しましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM
迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM導入 迅速なエンジニアリングでは、「思考のグラフ」とは、グラフ理論を使用してAIの推論プロセスを構造化および導く新しいアプローチを指します。しばしば線形sを含む従来の方法とは異なります
 Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM
Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM導入 おめでとう!あなたは成功したビジネスを運営しています。ウェブページ、ソーシャルメディアキャンペーン、ウェビナー、会議、無料リソース、その他のソースを通じて、毎日5000の電子メールIDを収集します。次の明白なステップはです
 Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM
Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM導入 今日のペースの速いソフトウェア開発環境では、最適なアプリケーションパフォーマンスが重要です。応答時間、エラーレート、リソース利用などのリアルタイムメトリックを監視することで、メインに役立ちます
 ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM
ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM「ユーザーは何人いますか?」彼は突き出した。 「私たちが最後に言ったのは毎週5億人のアクティブであり、非常に急速に成長していると思います」とアルトマンは答えました。 「わずか数週間で2倍になったと言った」とアンダーソンは続けた。 「私はそのprivと言いました
 PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM
PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM導入 Mistralは、最初のマルチモーダルモデル、つまりPixtral-12B-2409をリリースしました。このモデルは、Mistralの120億個のパラメーターであるNemo 12bに基づいて構築されています。このモデルを際立たせるものは何ですか?これで、画像とTexの両方を採用できます
 生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AM
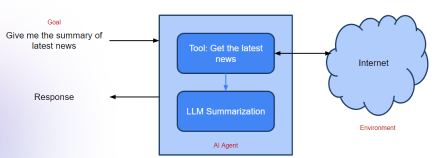
生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AMクエリに応答するだけでなく、情報を自律的に収集し、タスクを実行し、テキスト、画像、コードなどの複数のタイプのデータを処理するAIを搭載したアシスタントがいることを想像してください。未来的に聞こえますか?これでa
 金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM
金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM導入 金融業界は、効率的な取引と信用の可用性を促進することにより経済成長を促進するため、あらゆる国の発展の基礎となっています。取引の容易さとクレジット
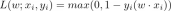 オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM
オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM導入 データは、ソーシャルメディア、金融取引、eコマースプラットフォームなどのソースから前例のないレートで生成されています。この連続的な情報ストリームを処理することは課題ですが、


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SublimeText3 Linux 新バージョン
SublimeText3 Linux 最新バージョン

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ZendStudio 13.5.1 Mac
強力な PHP 統合開発環境

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

EditPlus 中国語クラック版
サイズが小さく、構文の強調表示、コード プロンプト機能はサポートされていません







