- communauté
- Apprendre
- Bibliothèque d'outils
- Loisirs
Maison > Questions et réponses > le corps du texte
插入排序:对于随机排列长度为N且主见不重复的数组,平均情况下插入排序需要~N^2/4次比较以及~N^2/4。最坏情况下需要~N^2/2次比较和~N^2/2次交换。
第一个问题:想请教一下这个效率是怎么计算的?
希尔排序是基于插入排序所改进的算法。书上是这样描述的:中心思想是使数组中任意间隔为h的元素都是有序的。这样的数组被称为h有序数组。也就是说,一个h有序数组就是h个互相独立的有序数组编织在一起组成一个数组。
这样说我是能够理解的,但是它的代码有点令我难以理解。
//一些简单的通用性代码就不粘贴了,减少篇幅,以免各位看官看的烦
public static void sort(Comparable[] a) {
int n = a.length;
// 3x+1 increment sequence: 1, 4, 13, 40, 121, 364, 1093, ...
int h = 1;
while (h < n/3) h = 3*h + 1;
while (h >= 1) {
for (int i = h; i < n; i++) {、
//less是用来比较大小的,a[j]<[j-h]
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) {
//交换a[j]和a[j-h]的位置
exch(a, j, j-h);
}
}
assert isHsorted(a, h); //判断是否有序的代码
h /= 3;
}
assert isSorted(a);
}第二个问题是:h这个递增序列是什么意思?它有什么作用?为什么是h=3*h+1?
第三个问题是:书上说最坏的情况是N^(3/2)。N是数组大小。这个效率是如何计算出来的?
怪我咯2017-04-18 10:05:50
Question 1 :
Connaissances préalables :
La somme des n premiers termes de la suite arithmétique
Le tri par insertion commence à partir du 2ème élément. Lors du processus d'insertion, on peut voir que le pire des cas est le tri inversé. Il doit être exécuté 1+2+3+...+n-1 fois au total. D'après la somme des n premiers éléments, le résultat est (n-1)n/2 est approximativement égal à n^2/2. Des questions similaires peuvent être trouvées ici.
.Question 2 :
Connaissances préalables :
Calcul de la complexité de l'algorithme de tri par insertion (c'est-à-dire ci-dessus)
Compréhension du tri Shell
L'incrément de définition de h ici est de 3. Il n'y a aucune exigence obligatoire. L'incrément de h peut également être de 2
Exemple :

Remarque : Lorsque l'incrément est de 2, les deux tableaux [72 874 283 911 820] et [401 141 592 887 348] sont tous insérés et triés
.Question 3 :
Connaissances préalables : théorie des nombres详见<数据结构与算法分析_JAVA语言描述>定理7.4:
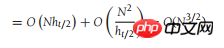
Résumé des recrues, un grand bravo.