Méthode détaillée de définition du domaine de fonction dans le carnet de croquis géométrique

Comment définir le domaine de la fonction carnet de croquis géométrique ? L'éditeur PHP Baicao partagera avec vous la méthode détaillée de définition du domaine de fonction dans le carnet de croquis géométrique pour vous aider à résoudre ce problème courant. Lisez le contenu suivant pour comprendre les étapes et précautions spécifiques.

Méthode 1 : utilisez le système de coordonnées du système pour construire l'image de la fonction et définissez le domaine pour contrôler la taille de l'image de la fonction du carnet de croquis géométrique.

1. Sélectionnez [Dessin] - [Dessiner une nouvelle fonction], dans l'éditeur [Nouvelle fonction], modifiez la fonction [f(x)=x3-2x-1], une fonction infinie apparaîtra après l'image [OK].

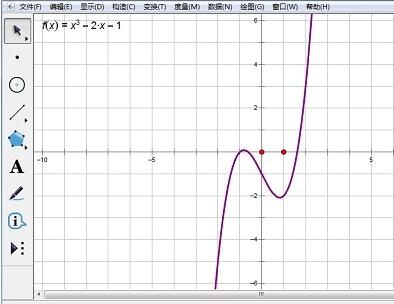
2. Cliquez avec le bouton droit sur l'image de la fonction, sélectionnez [Propriétés - [Dessin] - [Plage] et modifiez la plage de valeurs de x.

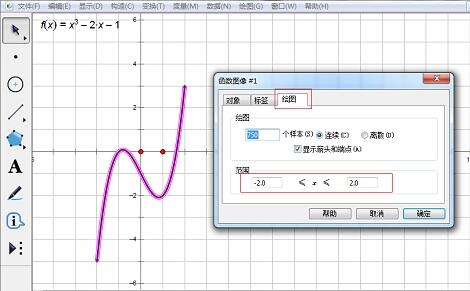
Conseils : Le x défini par cette méthode peut changer la taille de l'image en modifiant la plage. L'inconvénient est qu'il ne peut définir que des intervalles fermés.

Méthode 2 : utilisez [0 multiplication] pour modifier l'expression analytique de la fonction et changer le domaine de la fonction pour obtenir la taille d'image de la fonction spécifique.

1. Sélectionnez [Dessin] - [Dessiner une nouvelle fonction], dans l'éditeur [Nouvelle fonction], modifiez la fonction [f(x)=x3-2x-1], une fonction infinie apparaîtra après l'image [OK].

2. Double-cliquez sur l'expression analytique de la fonction et dans [Éditeur de fonctions], modifiez l'expression analytique selon le style indiqué dans l'image

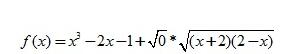
Conseils : sur la base de l'expression analytique originale, le les résultats des calculs sont ajoutés à la fin. Les calculs égaux à 0 ou indéfinis (sans signification) modifient le domaine de la nouvelle expression analytique de la fonction, atteignant ainsi l'objectif de dessiner l'image de la fonction dans une zone spécifique. [0 multiplication] Les expressions analytiques suivantes peuvent être modifiées de plusieurs manières, et des intervalles ouverts peuvent également être définis.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!