C’est l’un des problèmes non résolus les plus connus en mathématiques. Le nouveau travail a été évalué par des pairs et le texte intégral est disponible.
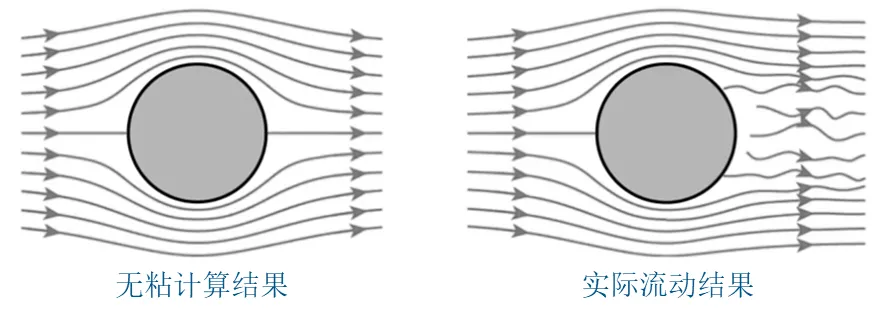
C’est en plein essor. La mécanique des fluides inaugure-t-elle son propre moment supraconducteur ? Ces derniers jours, les gens dans les cercles mathématiques discutent activement du fait que la formule hamiltonienne régulière du problème de Navier-Stokes est enfin apparue - ce problème non résolu de l'histoire des mathématiques pourrait avoir une réponse. Dans le passé, cela était même généralement considéré comme impossible. Quelle est l'importance de cela ? L'équation de Navier-Stokes, comme l'hypothèse de Riemann, a été répertoriée comme l'un des « sept problèmes mathématiques du millénaire » en 2000. Ces sept problèmes de classe mondiale sont : le problème NP-complet, la conjecture de Hodge, la conjecture de Poincaré, l'hypothèse de Riemann, l'existence de Yang-Mills et l'écart de masse, l'équation de Navier-Stokes, la conjecture de BSD. Chacun des sept problèmes est récompensé d'un million de dollars américains. En plus de 20 ans, seule la « conjecture de Poincaré » a été résolue par le talentueux mathématicien russe Perelman. La plupart d'entre eux sont familiers, mais "l'équation de Navier-Stokes" (équation N-S) semble être moins mentionnée parmi eux. La raison peut être que ce problème est trop difficile à comprendre (les étudiants ayant suivi le cours « Mécanique des Fluides » au collège auront certainement une idée). Certains pensent même qu’il s’agit de la formule la plus complexe de l’histoire des mathématiques. Pour faire simple, le mathématicien du XVIIIe siècle Euler a dérivé un ensemble d'équations dans "Principes généraux du mouvement des fluides" basées sur les changements de force et d'impulsion subis par le fluide lorsque le fluide non visqueux se déplace. La description de l’équation d’Euler stipule le mouvement du fluide dans un monde idéalisé, mais il existe une friction à l’intérieur du fluide réel. Les fluides dans la nature sont visqueux et sont collectivement appelés fluides visqueux ou fluides réels. Par exemple, lorsque nous remuons du miel, nous ressentons l'effet de viscosité, et la résistance du vol de l'avion dépend également en grande partie de la viscosité de l'air. En raison de la viscosité des fluides réels, notre étude du mouvement des fluides devient très compliquée. Au 19ème siècle, l'ingénieur et physicien français Claude-Louis Navit et le physicien et mathématicien irlandais George Stokes ont établi l'équilibre et le mouvement des fluides en considérant les forces intermoléculaires et décrivent la forme composante du mouvement en coordonnées cartésiennes. . C'est ce que les générations suivantes ont appelé l'équation de Navier-Stokes. L’une des équations aux dérivées partielles les plus effrayantes de tous les temps. Les équations de Navier-Stokes sont utilisées pour décrire des substances fluides comme les liquides et l'air. Ces équations relient la vitesse à laquelle l'élan des particules d'un fluide change (la force) aux changements de pression et aux forces visqueuses dissipatives (analogues au frottement) et à la gravité agissant à l'intérieur du fluide. Ces forces visqueuses résultent des interactions des molécules et nous indiquent la viscosité d’un liquide. De cette manière, les équations de Navier-Stokes décrivent l'équilibre dynamique des forces agissant sur une région donnée d'un liquide.
Cela est crucial pour de nombreux problèmes d'ingénierie.
S'il existe une solution globale au problème Navier-Stokes, de nombreuses technologies liées à la mécanique des fluides connaîtront des percées, notamment l'aérospatiale, les moteurs de fusée, la prévision météorologique, le transport par pipeline et la construction de flux sanguins médicaux. Module et ainsi de suite.
La difficulté avec cet ensemble d'équations est la suivante : comment l'expliquer en utilisant la théorie mathématique. Même la théorie mathématique qui explique les équations de champ d'Einstein décrivant les trous noirs exotiques est plus simple que la formulation des équations de Navier-Stokes.L'avancée importante mentionnée par les personnes provient de l'article "Une formulation canonique hamiltonienne du problème Navier-Stokes", qui a été publié dans la revue de premier plan "Journal of Fluid Mechanics" dans le domaine de la mécanique des fluides le 1er avril : Lien papier : https://www.cambridge.org/core/journals/journal-of-fluid-mechanics/article/canonical-hamiltonian-formulation-of-the-navierstokes-problem/B3EB9389AE700867A6A3EA63A45E69C6 Cet article propose une nouvelle formule hamiltonienne pour le problème isotrope de Navier-Stokes basée sur le principe de moindre action dérivé du principe des moindres carrés. La formule utilise la vitesse  et la pression
et la pression  comme quantités de champ variables, ainsi que l'impulsion conjuguée canonique dérivée de l'analyse. Sur cette base, cette étude construit une fonction hamiltonienne conservée H* qui satisfait l'équation canonique hamiltonienne et formule les équations hamiltoniennes-jacobiennes associées pour les écoulements compressibles et incompressibles. Cette équation hamiltonienne-jacobienne réduit le problème de la recherche de quatre quantités de champ indépendantes
comme quantités de champ variables, ainsi que l'impulsion conjuguée canonique dérivée de l'analyse. Sur cette base, cette étude construit une fonction hamiltonienne conservée H* qui satisfait l'équation canonique hamiltonienne et formule les équations hamiltoniennes-jacobiennes associées pour les écoulements compressibles et incompressibles. Cette équation hamiltonienne-jacobienne réduit le problème de la recherche de quatre quantités de champ indépendantes  à la recherche d'une seule fonctionnelle scalaire parmi ces champs - la fonctionnelle principale de Hamilton
à la recherche d'une seule fonctionnelle scalaire parmi ces champs - la fonctionnelle principale de Hamilton  De plus, les transformations hamiltonienne et jacobienne La théorie fournit une méthode prescrite pour résoudre le problème de Navier-Stokes : trouver S*. Si l'expression analytique de S * peut être obtenue, alors elle obtiendra un nouvel ensemble de champs par transformation canonique, donnant les expressions analytiques des champs de vitesse et de pression d'origine. Ces champs seront simplement équivalents à leurs champs initiaux. valeur. A défaut, on ne peut que prouver qu’une solution complète de l’équation de Hamilton-Jacobian existe ou n’existe pas, ce qui résoudrait également le problème de l’existence de la solution. Y a-t-il un prix d'un million de dollars pour cette nouvelle recherche ? Pour gagner, les chercheurs doivent démontrer qu’il existe des solutions aux équations tridimensionnelles incompressibles de Navier-Stokes et que, s’il existe des solutions, ces solutions sont lisses. Le mathématicien Terence Tao pensait un jour que c'était difficile. À en juger par les progrès actuels, de nouvelles recherches ont facilité la résolution de problèmes ouverts, et nous avons fait un grand pas en avant - nous avons réalisé la formule hamiltonienne régulière de l'équation de Navier-Stokes, cela pourrait signifier que nous peut contourner les limites du lagrangien standard et réduire le problème à la recherche d'une seule fonction scalaire. Peut-être ne sommes-nous pas loin de résoudre la deuxième question du puzzle du millénaire. https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/navier-strokes-equation/https : //zhuanlan.zhihu.com/p/263628141https://terrytao.wordpress.com/2007/03/18/why-global-regularity-for-navier-stokes-is-hard/
De plus, les transformations hamiltonienne et jacobienne La théorie fournit une méthode prescrite pour résoudre le problème de Navier-Stokes : trouver S*. Si l'expression analytique de S * peut être obtenue, alors elle obtiendra un nouvel ensemble de champs par transformation canonique, donnant les expressions analytiques des champs de vitesse et de pression d'origine. Ces champs seront simplement équivalents à leurs champs initiaux. valeur. A défaut, on ne peut que prouver qu’une solution complète de l’équation de Hamilton-Jacobian existe ou n’existe pas, ce qui résoudrait également le problème de l’existence de la solution. Y a-t-il un prix d'un million de dollars pour cette nouvelle recherche ? Pour gagner, les chercheurs doivent démontrer qu’il existe des solutions aux équations tridimensionnelles incompressibles de Navier-Stokes et que, s’il existe des solutions, ces solutions sont lisses. Le mathématicien Terence Tao pensait un jour que c'était difficile. À en juger par les progrès actuels, de nouvelles recherches ont facilité la résolution de problèmes ouverts, et nous avons fait un grand pas en avant - nous avons réalisé la formule hamiltonienne régulière de l'équation de Navier-Stokes, cela pourrait signifier que nous peut contourner les limites du lagrangien standard et réduire le problème à la recherche d'une seule fonction scalaire. Peut-être ne sommes-nous pas loin de résoudre la deuxième question du puzzle du millénaire. https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/navier-strokes-equation/https : //zhuanlan.zhihu.com/p/263628141https://terrytao.wordpress.com/2007/03/18/why-global-regularity-for-navier-stokes-is-hard/ Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
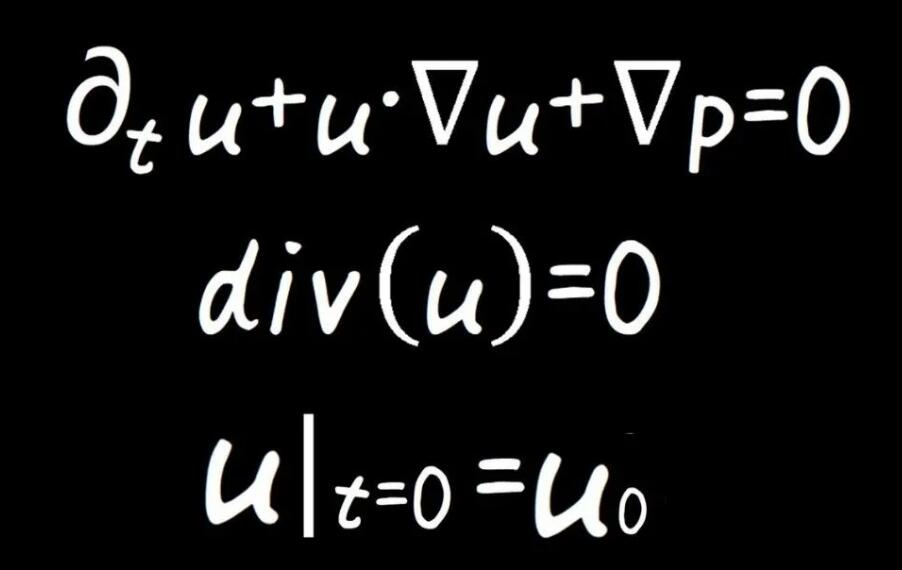

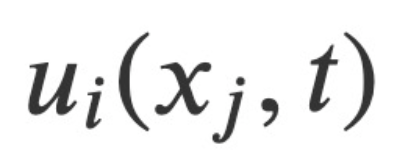 et la pression
et la pression 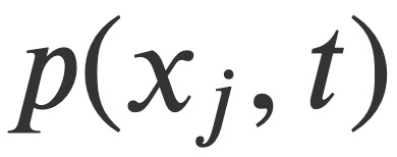 comme quantités de champ variables, ainsi que l'impulsion conjuguée canonique dérivée de l'analyse. Sur cette base, cette étude construit une fonction hamiltonienne conservée H* qui satisfait l'équation canonique hamiltonienne et formule les équations hamiltoniennes-jacobiennes associées pour les écoulements compressibles et incompressibles. Cette équation hamiltonienne-jacobienne réduit le problème de la recherche de quatre quantités de champ indépendantes
comme quantités de champ variables, ainsi que l'impulsion conjuguée canonique dérivée de l'analyse. Sur cette base, cette étude construit une fonction hamiltonienne conservée H* qui satisfait l'équation canonique hamiltonienne et formule les équations hamiltoniennes-jacobiennes associées pour les écoulements compressibles et incompressibles. Cette équation hamiltonienne-jacobienne réduit le problème de la recherche de quatre quantités de champ indépendantes 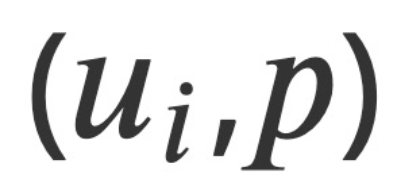 à la recherche d'une seule fonctionnelle scalaire parmi ces champs - la fonctionnelle principale de Hamilton
à la recherche d'une seule fonctionnelle scalaire parmi ces champs - la fonctionnelle principale de Hamilton 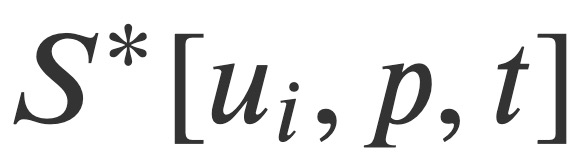 De plus, les transformations hamiltonienne et jacobienne La théorie fournit une méthode prescrite pour résoudre le problème de Navier-Stokes : trouver S*.
De plus, les transformations hamiltonienne et jacobienne La théorie fournit une méthode prescrite pour résoudre le problème de Navier-Stokes : trouver S*. 

