Le tri de Schram - apprendre à trier en fonction de l'équité

Lors de la conférence universitaire internationale AIBT 2023 qui s'est tenue en 2023, Ratidar Technologies LLC a publié un algorithme d'apprentissage par classement basé sur l'équité et a remporté le prix du meilleur rapport papier de la conférence. L'algorithme, appelé Skellam Rank, utilise pleinement les principes statistiques et combine la technologie de classement par paires et de décomposition matricielle pour résoudre les problèmes d'exactitude et d'équité du système de recommandation. Puisqu'il existe peu d'algorithmes d'apprentissage de classement innovants dans les systèmes de recommandation, l'algorithme de classement de Schramam a si bien fonctionné qu'il a remporté un prix de recherche lors de la conférence. Les principes de base de l'algorithme de Schram seront présentés ci-dessous :

Rappelons d'abord la distribution de Poisson :

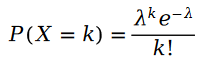
La formule de calcul des paramètres de la distribution de Poisson est la suivante :

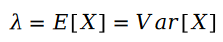
Deux La différence des variables de Poisson est la distribution de Schram :

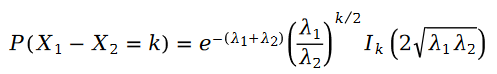
Dans la formule, nous avons :

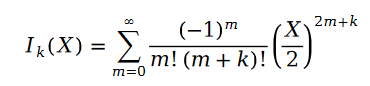
La fonction est appelée fonction de Bessel de première espèce.

Avec ces concepts les plus fondamentaux en statistiques, construisons un système de recommandation d'apprentissage par classement par paire !

Nous pensons d'abord que l'évaluation des éléments par l'utilisateur est un concept de distribution de Poisson. En d'autres termes, la valeur d'évaluation des éléments utilisateur obéit à la distribution de probabilité suivante :

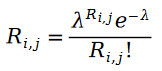
La raison pour laquelle nous pouvons décrire le processus d'évaluation des éléments par les utilisateurs comme un processus de Poisson est qu'il existe un effet Matthieu dans l'évaluation des éléments utilisateur, c'est-à-dire que les utilisateurs avec des notes plus élevées ont plus de notes, de sorte que nous pouvons utiliser le nombre de personnes qui notent un élément pour approximer la répartition des notes pour cet élément. À quel processus aléatoire obéit le nombre de personnes qui évaluent un article ? Naturellement, nous penserons au processus de Poisson. Étant donné que la probabilité qu'un utilisateur évalue un élément est similaire à la probabilité du nombre de personnes qui ont évalué cet élément, nous pouvons naturellement utiliser le processus de Poisson pour approximer le processus par lequel les utilisateurs notent un élément.

Nous remplacerons les paramètres du processus de Poisson par les statistiques des exemples de données et obtiendrons la formule suivante :

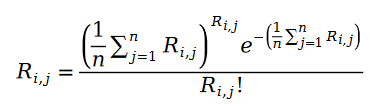
Nous définirons ci-dessous la formule de la fonction de maximum de vraisemblance du classement Pariwise. Comme nous le savons tous, le soi-disant classement par paires signifie que nous utilisons la fonction du maximum de vraisemblance pour résoudre les paramètres du modèle, afin que le modèle puisse maintenir au maximum la relation entre les paires de classement connues dans l'échantillon de données :

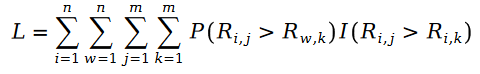
car R dans la formule est la distribution de Poisson, donc leur différence est la distribution de Schramam, c'est-à-dire :

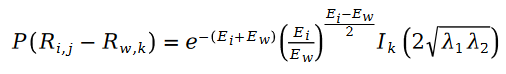
où la variable E est définie comme suit :

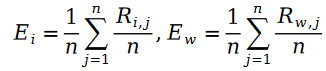
Nous appelons la distribution de Schramam La formule est introduite dans la fonction de perte L de la fonction de maximum de vraisemblance, et la formule suivante est obtenue :

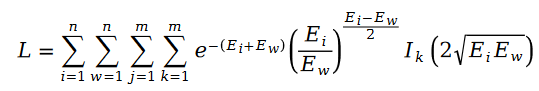
Dans la valeur de notation utilisateur R qui apparaît dans la variable E, nous utilisons la décomposition matricielle pour le résoudre. Utilisez le paramètre vecteur de caractéristiques utilisateur U et le vecteur de caractéristiques d'élément V dans la décomposition matricielle comme variables à résoudre :

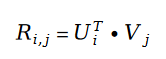
Nous passons d'abord en revue ici le concept de factorisation matricielle. Le concept de factorisation matricielle est un algorithme de système de recommandation proposé vers 2010. Cet algorithme peut être considéré comme l'un des algorithmes de système de recommandation les plus réussis de l'histoire. À ce jour, un grand nombre d'entreprises de systèmes de recommandation utilisent encore l'algorithme de décomposition matricielle comme base de référence pour les systèmes en ligne, et Factorization Machine, un composant important de l'algorithme de recommandation classique populaire DeepFM, est également une amélioration ultérieure de l'algorithme de décomposition matricielle dans le L'algorithme du système de recommandation. La version est inextricablement liée à la décomposition matricielle. Il existe un article historique sur l'algorithme de factorisation matricielle, à savoir Factorisation matricielle probabiliste en 2007. L'auteur a utilisé un modèle d'apprentissage statistique pour remodeler le concept de factorisation matricielle en algèbre linéaire, donnant pour la première fois à la factorisation matricielle une base théorique mathématique solide.

Le concept de base de la décomposition matricielle est d'utiliser le produit scalaire de vecteurs pour prédire efficacement les évaluations des utilisateurs inconnus tout en réduisant la dimensionnalité de la matrice des évaluations des utilisateurs. La fonction de perte de la décomposition matricielle est la suivante :

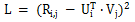
Il existe de nombreuses variantes de l'algorithme de décomposition matricielle. Par exemple, la SVDFeature proposée par l'Université Jiao Tong de Shanghai modélise les vecteurs U et V sous forme de combinaisons linéaires. , de sorte que le problème de décomposition matricielle devient le problème de l'ingénierie des fonctionnalités. SVDFeature est également un article phare dans le domaine de la factorisation matricielle. La décomposition matricielle peut être appliquée dans le classement par paires pour remplacer les évaluations d'utilisateurs inconnus afin d'atteindre des objectifs de modélisation. Les cas d'application classiques incluent l'algorithme BPR-MF dans le classement par paires bayésien, et l'algorithme de classement Schramam s'appuie sur les mêmes idées.

Nous utilisons la descente de gradient stochastique pour résoudre l'algorithme de tri de Schramam. Étant donné que la descente de gradient stochastique peut grandement simplifier la fonction de perte dans le processus de résolution pour atteindre l'objectif de la solution, notre fonction de perte devient la formule suivante :

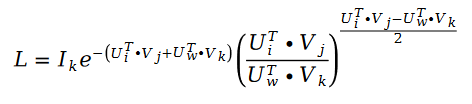
Utilisez la descente de gradient stochastique pour calculer les paramètres inconnus U et la résolution de V. , on obtient la formule itérative comme suit :

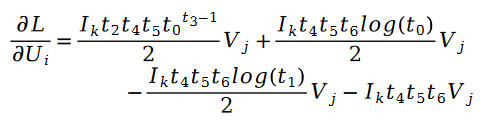
Parmi eux :

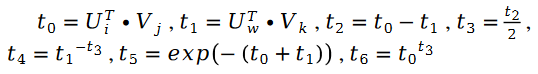
En plus :

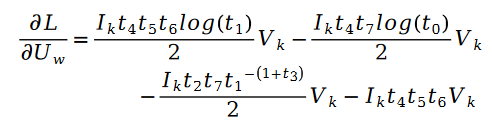
parmi eux :

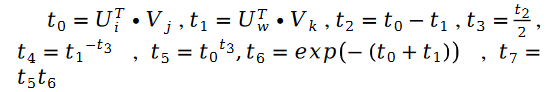
Pour les variables de paramètres inconnues La solution de V est similaire, nous avons la formule suivante :

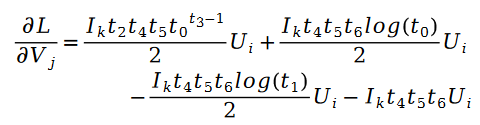
Parmi elles :

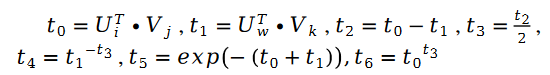
En plus :

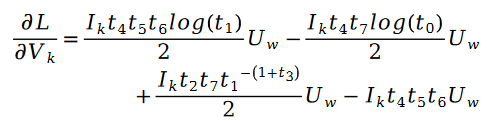
parmi lesquelles :

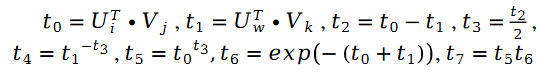
L'ensemble du processus algorithmique, nous utilisons le pseudo-code suivant pour démontrer :

Afin de vérifier l'efficacité de l'algorithme, l'auteur de l'article l'a testé sur l'ensemble de données MovieLens 1 Million et l'ensemble de données LDOS-CoMoDa. Le premier ensemble de données contient les évaluations de 6 040 utilisateurs et 3 706 films. L'ensemble des données de classification contient environ 1 million de données de classification et constitue l'une des collections de données de classification les plus connues dans le domaine des systèmes de recommandation. La deuxième collecte de données provient de Slovénie et constitue une collecte de données basée sur un système de recommandation basé sur des scénarios, ce qui est rare sur Internet. L'ensemble de données contient les évaluations de 121 utilisateurs et 1 232 films. L'auteur a comparé le tri de Schram avec 9 autres algorithmes du système de recommandation. Les principaux indicateurs d'évaluation sont le MAE (Mean Absolute Error, utilisé pour tester l'exactitude) et le degré d'effet Matthew (principalement utilisé pour tester l'équité) :

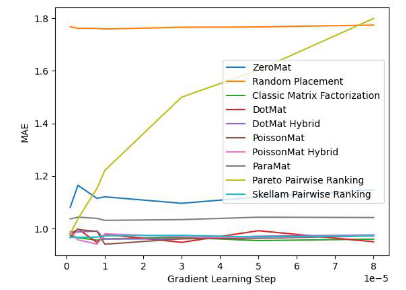
Figure 1. . Ensemble de données MovieLens 1 million (indicateur MAE)

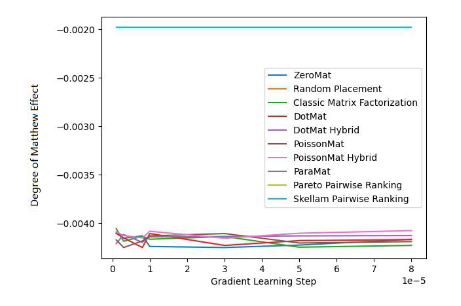
Figure 2. Ensemble de données MovieLens 1 million (indicateur de l'effet Degré de Matthieu)

Grâce aux figures 1 et 2, nous avons constaté que le tri de Schram fonctionnait bien sur le MAE. indicateur, mais pendant toute l’expérience de Grid Search, il n’était pas toujours garanti qu’il fonctionnerait mieux que les autres algorithmes. Mais dans la figure 2, nous constatons que le tri de Schram est en tête de l'indice d'équité, loin devant les 9 autres algorithmes du système de recommandation. Jetez un coup d'œil aux performances de cet algorithme sur l'ensemble de données LDOS-COMODA:

Figure 3. ensemble de données LDOS-COMODA (indicateur MAE)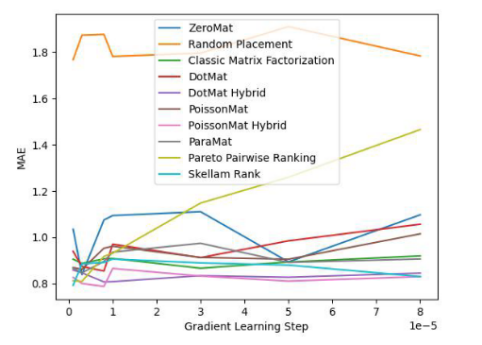

Figure 4. Ensemble de données LDOS- CoMoDa (indicateur de l'effet du degré de Matthieu)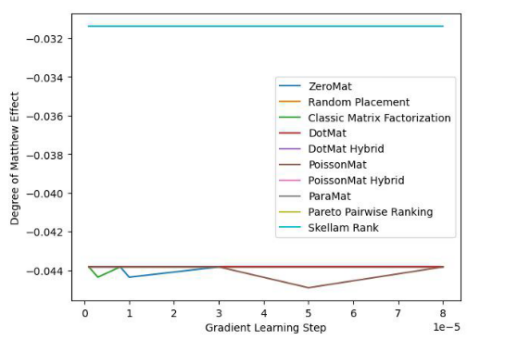

Grâce aux figures 3 et 4, nous comprenons que le tri Schillam est le meilleur dans l'indicateur d'équité et fonctionne bien dans l'indicateur de précision. La conclusion est similaire à l’expérience précédente.

Le tri Schramm combine des concepts tels que la distribution de Poisson, la décomposition matricielle et le classement par paires, et est un algorithme d'apprentissage de classement rare pour les systèmes de recommandation. Dans le domaine technique, ceux qui maîtrisent la technologie d'apprentissage par classement ne représentent que 1/6 de ceux qui maîtrisent le deep learning, l'apprentissage par classement est donc une technologie rare. Et il y a encore moins de talents capables d’inventer un apprentissage original du classement dans le domaine des systèmes de recommandation. L'algorithme d'apprentissage du classement libère les gens de la perspective étroite de la prédiction des scores et leur fait comprendre que la chose la plus importante est l'ordre, pas le score. L'apprentissage par classement basé sur l'équité est actuellement très populaire dans le domaine de la recherche d'informations, en particulier dans les grandes conférences telles que SIGIR. Les articles sur les systèmes de recommandation basés sur l'équité sont les bienvenus et espèrent attirer l'attention des lecteurs.

À propos de l'auteur

Wang Hao, ancien chef du laboratoire d'intelligence artificielle Funplus. Il a occupé des postes de direction en matière de technologie et de technologie chez ThoughtWorks, Douban, Baidu, Sina et d'autres sociétés. Ayant travaillé dans des sociétés Internet, des technologies financières, des jeux et d'autres sociétés pendant 12 ans, il possède des connaissances approfondies et une riche expérience dans des domaines tels que l'intelligence artificielle, l'infographie et la blockchain. A publié 42 articles dans des conférences et revues universitaires internationales et a remporté le prix du meilleur article IEEE SMI 2008 et le prix du meilleur article ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!