Trois articles résolvent le problème de « l'optimisation et de l'évaluation de la segmentation sémantique » ! Louvain/Tsinghua/Oxford et d'autres ont proposé conjointement une nouvelle méthode

Les fonctions de perte couramment utilisées pour optimiser les modèles de segmentation sémantique incluent la perte Soft Jaccard, la perte Soft Dice et la perte Soft Tversky. Cependant, ces fonctions de perte sont incompatibles avec les étiquettes souples et ne peuvent donc pas prendre en charge certaines techniques de formation importantes telles que le lissage des étiquettes, la distillation des connaissances, l'apprentissage semi-supervisé et les annotateurs multiples. Ces techniques de formation sont très importantes pour améliorer les performances et la robustesse des modèles de segmentation sémantique, c'est pourquoi des recherches supplémentaires et une optimisation des fonctions de perte sont nécessaires pour soutenir l'application de ces techniques de formation.

D'autre part, les indicateurs d'évaluation de segmentation sémantique couramment utilisés incluent mAcc et mIoU. Cependant, ces indicateurs ont une préférence pour les objets plus gros, ce qui affecte sérieusement l'évaluation des performances de sécurité du modèle.

Pour résoudre ces problèmes, des chercheurs de l'Université de Louvain et de Tsinghua ont d'abord proposé la perte JDT. La perte JDT est un réglage fin de la fonction de perte d'origine, qui comprend la perte métrique Jaccard, la perte semimétrique Dice et la perte Tversky compatible. La perte JDT est égale à la fonction de perte d'origine lorsqu'il s'agit d'étiquettes rigides et est également entièrement applicable aux étiquettes souples. Cette amélioration rend la formation du modèle plus précise et plus stable.

Les chercheurs ont appliqué avec succès la perte JDT dans quatre scénarios importants : le lissage des étiquettes, la distillation des connaissances, l'apprentissage semi-supervisé et plusieurs annotateurs. Ces applications démontrent la puissance de la perte JDT pour améliorer la précision et l'étalonnage des modèles.

Photos

Lien papier : https://arxiv.org/pdf/2302.05666.pdf

Photos

Lien papier : https://arxiv.org/pdf/2303 .16296 .pdf

De plus, les chercheurs ont également proposé des indicateurs d'évaluation plus fins. Ces mesures d'évaluation fines sont moins biaisées par rapport aux objets de grande taille, fournissent des informations statistiques plus riches et peuvent fournir des informations précieuses pour l'audit des modèles et des ensembles de données.

Et les chercheurs ont mené une étude de référence approfondie, soulignant la nécessité que les évaluations ne soient pas basées sur une seule métrique, et ont découvert le rôle important de la structure du réseau neuronal et de la perte JDT dans l'optimisation des métriques fines.

Photos

Lien papier : https://arxiv.org/pdf/2310.19252.pdf

Lien code : https://github.com/zifuwanggg/JDTLosses

Pertes existantes Fonctions

Étant donné que l'indice Jaccard et le score de dés sont définis sur des ensembles, ils ne sont pas différenciables. Afin de les rendre différentiables, il existe actuellement deux approches courantes : l'une consiste à utiliser la relation entre l'ensemble et le module Lp du vecteur correspondant, comme la perte Soft Jaccard (SJL), la perte Soft Dice (SDL) et Soft Tversky. perte (STL).

Ils écrivent la taille de l'ensemble comme module L1 du vecteur correspondant, et écrivent l'intersection de deux ensembles comme produit scalaire des deux vecteurs correspondants. L'autre consiste à utiliser la propriété sous-modulaire de Jaccard Index pour effectuer une expansion de Lovasz sur la fonction définie, telle que la perte Lovasz-Softmax (LSL).

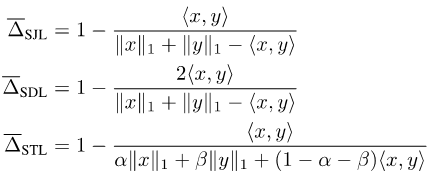Images

Ces fonctions de perte supposent que la sortie x du réseau neuronal est un vecteur continu et que l'étiquette y est un vecteur binaire discret. Si l'étiquette est une étiquette souple, c'est-à-dire lorsque y n'est plus un vecteur binaire discret, mais un vecteur continu, ces fonctions de perte ne sont plus compatibles.

Prenons SJL comme exemple, considérons un cas simple à un seul pixel :

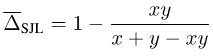picture

On peut constater que pour tout y > 0, SJL sera minimisé à x = 1. , et est maximisé lorsque x = 0. Puisqu’une fonction de perte doit être minimisée lorsque x = y, cela est évidemment déraisonnable.

Fonction de perte compatible avec les étiquettes souples

Afin de rendre la fonction de perte d'origine compatible avec les étiquettes souples, il est nécessaire d'introduire la différence symétrique des deux ensembles lors du calcul de l'intersection et de l'union des deux ensembles :

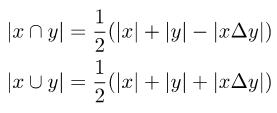Image

Notez que la différence symétrique entre deux ensembles peut s'écrire comme le module L1 de la différence entre les deux vecteurs correspondants :

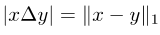Photos

En rassemblant ce qui précède, nous proposons la perte JDT. Il s'agit d'une variante de SJL, Jaccard Metric loss (JML), d'une variante de SDL, Dice Semimetric loss (DML) et d'une variante de STL, Compatible Tversky loss (CTL).

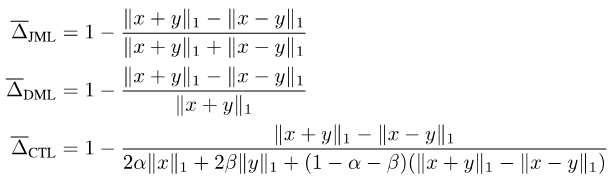Photos

Propriétés de la perte JDT

Nous avons prouvé que la perte JDT a les propriétés suivantes.

Propriété 1 : JML est une métrique et DML est une semimétrique.

Propriété 2 : lorsque y est une étiquette dure, JML est équivalent à SJL, DML est équivalent à SDL et CTL est équivalent à STL.

Propriété 3 : lorsque y est une étiquette logicielle, JML, DML et CTL sont tous compatibles avec les étiquettes logicielles, c'est-à-dire x = y ó f(x, y) = 0.

En raison de la propriété 1, elles sont également appelées perte métrique Jaccard et perte semimétrique Dice. La propriété 2 montre que dans les scénarios généraux où seules des étiquettes strictes sont utilisées pour la formation, la perte JDT peut être directement utilisée pour remplacer la fonction de perte existante sans entraîner de modifications.

Comment utiliser la perte JDT

Nous avons mené de nombreuses expériences et résumé quelques précautions d'utilisation de la perte JDT.

Remarque 1 : Sélectionnez la fonction de perte correspondante en fonction de l'indice d'évaluation. Si l'indice d'évaluation est Jaccard Index, alors JML doit être sélectionné ; si l'indice d'évaluation est Dice Score, alors DML doit être sélectionné si vous souhaitez attribuer des poids différents aux faux positifs et aux faux négatifs, alors CTL doit être sélectionné ; Deuxièmement, lors de l'optimisation des indicateurs d'évaluation à granularité fine, la perte JDT doit également être modifiée en conséquence.

Remarque 2 : Combinez la perte JDT et la fonction de perte au niveau des pixels (telle que la perte d'entropie croisée, la perte focale). Cet article a révélé que 0,25CE + 0,75JDT est généralement un bon choix.

Remarque 3 : Il est préférable d'utiliser une période plus courte pour l'entraînement. Après avoir ajouté la perte JDT, cela ne nécessite généralement que la moitié des époques de formation sur la perte d'entropie croisée.

Remarque 4 : lors de l'exécution d'un entraînement distribué sur plusieurs GPU, s'il n'y a pas de communication supplémentaire entre les GPU, la perte JDT optimisera de manière incorrecte les métriques d'évaluation fines, ce qui entraînera de mauvaises performances sur le mIoU traditionnel.

Remarque 5 : Lors d'un entraînement sur un ensemble de données avec un déséquilibre extrême des catégories, veuillez noter que la perte JDL est calculée séparément sur chaque catégorie puis moyennée, ce qui peut rendre l'entraînement instable.

Résultats expérimentaux

Des expériences ont prouvé que, par rapport à la ligne de base de perte d'entropie croisée, l'ajout de perte JDT peut améliorer efficacement la précision du modèle lors de l'entraînement avec des étiquettes dures. La précision et l'étalonnage du modèle peuvent être encore améliorés en introduisant des étiquettes souples.

Photos

En ajoutant uniquement le terme de perte JDT lors de la formation, cet article a atteint SOTA en distillation de connaissances, apprentissage semi-supervisé et multi-annotateurs en segmentation sémantique.

Pictures

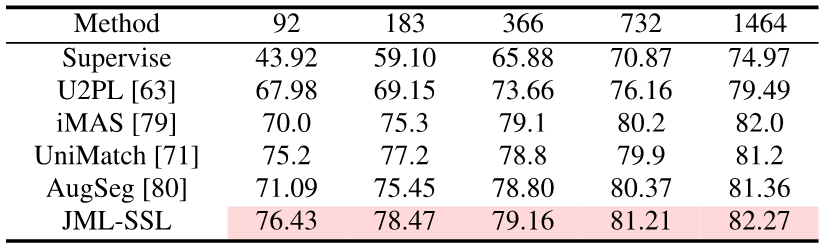Pictures

Pictures

Mesures d'évaluation existantes

La segmentation sémantique est une tâche de classification au niveau des pixels, donc chaque précision de pixel : pixel global sage précision (Acc). Cependant, comme Acc sera biaisé en faveur de la catégorie majoritaire, PASCAL VOC 2007 adopte un indice d'évaluation qui calcule séparément la précision des pixels de chaque catégorie, puis en fait la moyenne : précision moyenne par pixel (mAcc).

Mais comme mAcc ne prend pas en compte les faux positifs, depuis PASCAL VOC 2008, le taux moyen d'intersection et d'union (par ensemble de données mIoU, mIoUD) a été utilisé comme indice d'évaluation. PASCAL VOC a été le premier ensemble de données à introduire la tâche de segmentation sémantique, et les indicateurs d'évaluation qu'il a utilisés ont été largement utilisés dans divers ensembles de données ultérieurs.

Plus précisément, IoU peut s'écrire comme :

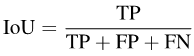Photos

Afin de calculer mIoUD, nous devons d'abord compter les vrais positifs (vrai positif, TP) et les faux positifs (faux positifs, FP) de toutes les photos I dans l'ensemble des données pour chaque catégorie. c Et faux négatif (FN) :

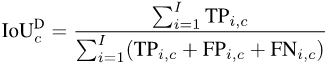Photos

Après avoir la valeur numérique pour chaque catégorie, on fait la moyenne par catégorie, éliminant ainsi la préférence pour la catégorie majoritaire :

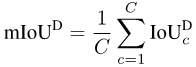Photos

Parce que mIoUD additionne les TP, FP et FN de tous les pixels de l'ensemble de données, il sera inévitablement biaisé en faveur de ces objets de grande taille.

Dans certains scénarios d'application avec des exigences de sécurité élevées, comme la conduite autonome et les images médicales, il y a souvent des objets petits mais qui ne peuvent être ignorés.

Comme le montre l'image ci-dessous, la taille des voitures sur différentes photos est évidemment différente. Par conséquent, la préférence de mIoUD pour les objets de grande taille affectera sérieusement son évaluation des performances de sécurité du modèle.

Indicateurs d'évaluation à granularité fine

Afin de résoudre le problème du mIoUD, nous proposons des indicateurs d'évaluation à granularité fine. Ces mesures calculent l'IoU sur chaque photo séparément, ce qui peut réduire efficacement la préférence pour les objets de grande taille.

mIoUI

Pour chaque catégorie c, nous calculons un IoU sur chaque photo i :

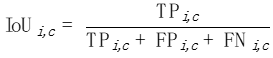picture

Ensuite, pour chaque photo i, nous faisons la moyenne de toutes les catégories apparues sur cette photo :

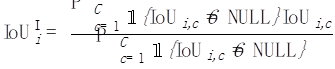images

Enfin, nous faisons la moyenne des valeurs de toutes les photos :

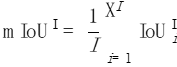images

mIoUC

De même, après avoir calculé l'IoU de chaque catégorie c sur chaque photo i, on peut faire la moyenne de toutes les photos dans lesquelles chaque catégorie c apparaît :

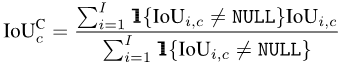
Enfin, faire la moyenne des valeurs de toutes les catégories :

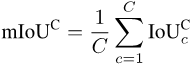
Étant donné que toutes les catégories n'apparaîtront pas sur toutes les photos, des valeurs NULL apparaîtront pour certaines combinaisons de catégories et de photos, comme le montre la figure ci-dessous. Lors du calcul de mIoUI, la moyenne des catégories est d'abord calculée, puis la moyenne des photos est effectuée, tandis que lorsque mIoUC est calculé, la moyenne des photos est effectuée en premier, puis la moyenne des catégories est effectuée.

Le résultat est que mIoUI peut être biaisé en faveur des catégories qui apparaissent fréquemment (comme C1 dans la figure ci-dessous), ce qui n'est généralement pas bon. Mais d'un autre côté, lors du calcul de mIoUI, étant donné que chaque photo a une valeur IoU, cela peut nous aider à effectuer un audit et une analyse du modèle et de l'ensemble de données.

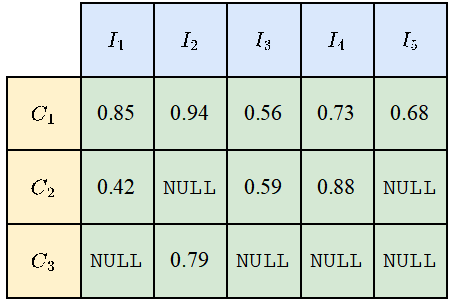Photos

Indicateurs d'évaluation du pire cas

Pour certains scénarios d'application axés sur la sécurité, nous sommes souvent plus préoccupés par la qualité de la segmentation dans le pire des cas, tandis que les indicateurs à granularité fine L'un des avantages est la capacité de calculer les indicateurs correspondants du pire cas. Prenons mIoUC comme exemple. Une méthode similaire peut également calculer l'indicateur du pire cas correspondant de mIoUI.

Pour chaque catégorie c, nous trions d'abord les valeurs IoU​​de toutes les photos dans lesquelles elle est apparue (en supposant qu'il existe de telles photos Ic) par ordre croissant. Ensuite, nous définissons q comme étant un petit nombre, tel que 1 ou 5. Ensuite, on utilise uniquement le top Ic*q% des photos triées pour calculer la valeur finale :

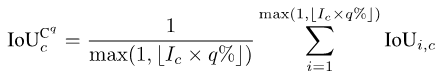Photos

Après avoir la valeur de chaque classe c, on peut trier par catégorie comme avant Moyenne ceci pour obtenir la métrique du pire des cas de mIoUC.

Résultats expérimentaux

Nous avons formé 15 modèles sur 12 ensembles de données et avons découvert les phénomènes suivants.

Phénomène 1 : Aucun modèle ne peut obtenir les meilleurs résultats sur tous les indicateurs d'évaluation. Chaque indice d'évaluation a un objectif différent, nous devons donc considérer plusieurs indices d'évaluation en même temps pour mener une évaluation complète.

Phénomène 2 : Il y a des photos dans certains ensembles de données qui font que presque tous les modèles atteignent une valeur IoU très faible. Cela est en partie dû au fait que les photos elles-mêmes sont très difficiles, comme certains objets très petits et un fort contraste entre la lumière et l'obscurité, et en partie parce qu'il y a des problèmes avec les étiquettes de ces photos. Par conséquent, des mesures d'évaluation fines peuvent nous aider à effectuer des audits de modèles (trouver des scénarios dans lesquels les modèles commettent des erreurs) et des audits d'ensembles de données (trouver de mauvaises étiquettes).

Phénomène 3 : La structure du réseau neuronal joue un rôle crucial dans l'optimisation des indicateurs d'évaluation à granularité fine. D'une part, l'amélioration du champ de réception apportée par des structures telles que ASPP (adoptées par DeepLabV3 et DeepLabV3+) peut aider le modèle à reconnaître des objets de grande taille, améliorant ainsi efficacement la valeur de mIoUD, d'autre part, l'écart entre ; encodeur et décodeur Les connexions longues (adoptées par UNet et DeepLabV3+) permettent au modèle de reconnaître les objets de petite taille, améliorant ainsi la valeur des indicateurs d'évaluation à granularité fine.

Phénomène 4 : La valeur de l'indicateur du pire cas est bien inférieure à la valeur de l'indicateur moyen correspondant. Le tableau suivant montre le mIoUC et les valeurs correspondantes de l'indicateur du pire cas de DeepLabV3-ResNet101 sur plusieurs ensembles de données. Une question à considérer à l'avenir est la suivante : comment devrions-nous concevoir la structure du réseau neuronal et la méthode d'optimisation pour améliorer les performances du modèle dans les pires indicateurs ?

Photos

Phénomène 5 : La fonction de perte joue un rôle crucial dans l'optimisation des indicateurs d'évaluation à granularité fine. Par rapport au test de perte d'entropie croisée, comme indiqué dans (0, 0, 0) dans le tableau suivant, lorsque les indicateurs d'évaluation deviennent à granularité fine, l'utilisation de la fonction de perte correspondante peut considérablement améliorer les performances du modèle lors d'une évaluation à granularité fine. indicateurs. Par exemple, sur ADE20K, la différence de perte mIoUC entre JML et Cross Entropy sera supérieure à 7 %.

Pictures

Future Work

Nous avons uniquement considéré la perte JDT comme la fonction de perte sur la segmentation sémantique, mais elles peuvent également être appliquées à d'autres tâches, telles que les tâches de classification traditionnelles.

Deuxièmement, les pertes JDT ne sont utilisées que dans l'espace des étiquettes, mais nous pensons qu'elles peuvent être utilisées pour minimiser la distance entre deux vecteurs quelconques dans l'espace des fonctionnalités, comme le remplacement du module Lp et de la distance cosinus.

Références :

https://arxiv.org/pdf/2302.05666.pdf

https://arxiv.org/pdf/2303.16296.pdf

https://arxiv.org/pdf/2310.19252 . pdf

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!