Une analyse approfondie des principes de l'algorithme BFS, avec des explications illustrées et du code Python pour implémenter l'algorithme BFS.

BFS, également connu sous le nom de recherche en largeur, est un algorithme récursif comme l'algorithme DFS. La différence est que l'algorithme BFS utilise une file d'attente pour parcourir tous les nœuds cibles tout en évitant les boucles.

Illustration du principe de fonctionnement de l'algorithme BFS

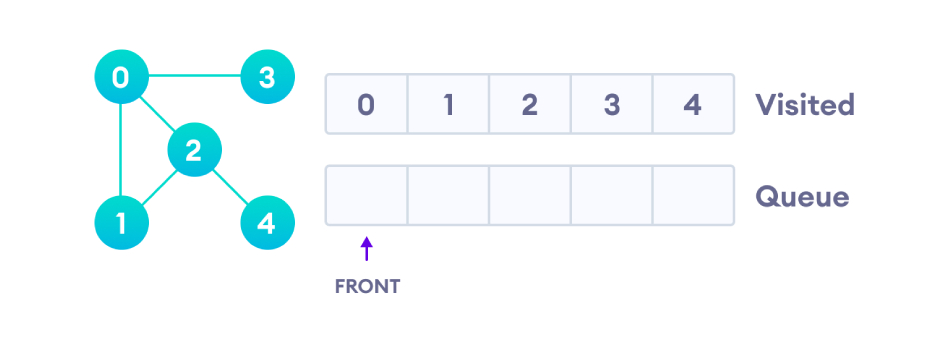
Prenons comme exemple un graphe non orienté avec 5 nœuds, comme indiqué ci-dessous :

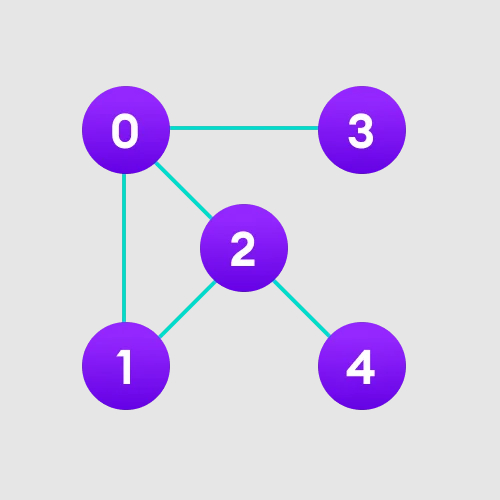
À partir du nœud 0, l'algorithme BFS le met d'abord dans la liste Visité et tous les nœuds voisins sont mis dans une file d'attente.

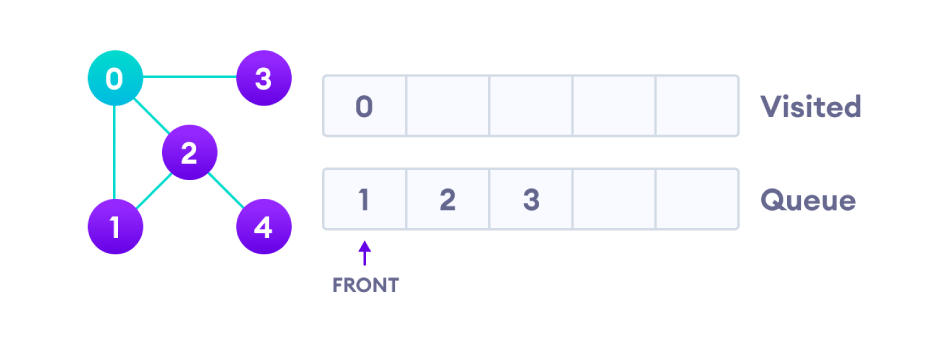
Ensuite, visitez le nœud 1 en tête de la file d'attente et accédez aux nœuds adjacents au nœud 1. Le nœud 0 ayant déjà été visité, le nœud 2 est visité.

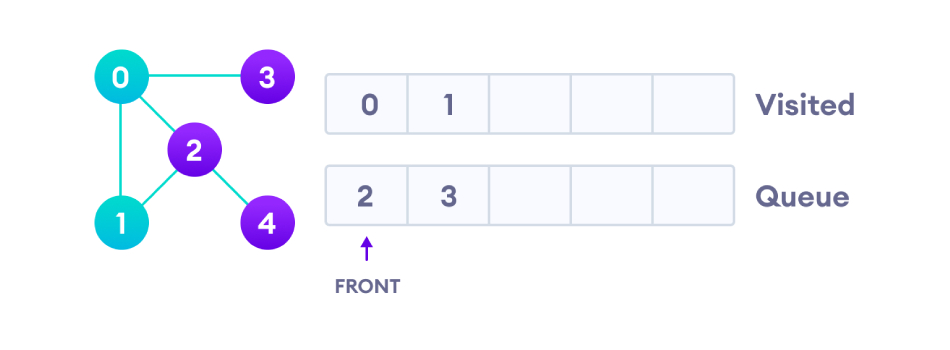
Le nœud 2 a un nœud voisin 4 non visité, mais comme le nœud 4 est à la fin de la file d'attente, nous voulons d'abord visiter le nœud 3 en tête de la file d'attente.

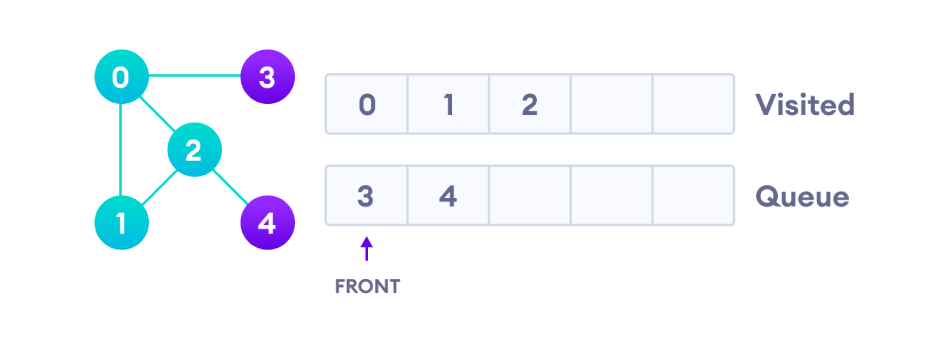
Seul le nœud 4 reste dans la file d'attente qui n'a pas été visité, donc le nœud 4 est visité en dernier.

À ce stade, le parcours en largeur de ce graphe non orienté est terminé.

Pseudocode de l'algorithme BFS

create a queue Q 
mark v as visited and put v into Q 
while Q is non-empty 
remove the head u of Q 
mark and enqueue all (unvisited) neighbours of u

Code Python pour implémenter l'algorithme BFS

import collections
def bfs(graph, root):
    visited, queue = set(), collections.deque([root])
    visited.add(root)

while queue:
        vertex = queue.popleft()
        print(str(vertex) + " ", end="")

        for neighbour in graph[vertex]:
            if neighbour not in visited:
                visited.add(neighbour)
                queue.append(neighbour)

if __name__ == '__main__':
    graph = {0: [1, 2], 1: [2], 2: [3], 3: [1, 2]}
    print("Following is Breadth First Traversal: ")
    bfs(graph, 0)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!