
La régularisation laplacienne est une méthode courante de régularisation de modèle d'apprentissage automatique utilisée pour empêcher le surajustement du modèle. Son principe est de limiter la complexité du modèle en ajoutant un terme de pénalité L1 ou L2 à la fonction de perte du modèle, afin que le modèle ne surajuste pas les données d'entraînement et améliore la capacité de généralisation du modèle.
En machine learning, le but d'un modèle est de trouver une fonction qui correspond le mieux aux données connues. Cependant, une dépendance excessive à l’égard des données d’entraînement peut entraîner de mauvaises performances sur les données de test, ce que l’on appelle le surapprentissage. Une des causes du surajustement est que le modèle est trop complexe, peut-être avec trop de paramètres ou de fonctionnalités libres. Afin d'éviter le surajustement, nous devons contraindre la complexité du modèle, ce qui est le rôle de la régularisation. Avec la régularisation, nous pouvons limiter le nombre de paramètres ou de fonctionnalités du modèle, empêchant ainsi le surajustement des données d'entraînement. Cette contrainte peut être obtenue en introduisant un terme de régularisation, qui pénalise la complexité du modèle lors du processus d'optimisation pour trouver un point d'équilibre plus approprié. Il existe de nombreuses méthodes de régularisation, telles que la régularisation L1 et la régularisation L2. Le choix d'une méthode de régularisation appropriée peut améliorer la capacité de généralisation du modèle et lui permettre de mieux fonctionner sur des données inconnues.
L'idée principale de la régularisation laplacienne est de contraindre la complexité du modèle en ajoutant un terme de pénalité L1 ou L2 à la fonction de perte du modèle. Ces termes de pénalité sont calculés en multipliant le paramètre de régularisation par la norme L1 ou L2 des paramètres du modèle, également appelée décroissance du poids. Le paramètre de régularisation est un hyperparamètre qui doit être ajusté pendant l'entraînement pour trouver le degré de régularisation optimal. En introduisant la régularisation, le modèle peut mieux résoudre le problème de surajustement et améliorer la capacité de généralisation du modèle.
Le terme de pénalité dans la régularisation L1 est la somme des valeurs absolues de tous les éléments du vecteur poids. Par conséquent, la régularisation L1 peut encourager certains poids à devenir nuls, réalisant ainsi une sélection de fonctionnalités, c'est-à-dire la suppression de fonctionnalités qui ne sont pas importantes pour le modèle. Cette caractéristique permet à la régularisation L1 de bien fonctionner sur des ensembles de données de grande dimension, réduisant le nombre de fonctionnalités et améliorant la capacité de généralisation du modèle.
Le terme de pénalité dans la régularisation L2 est la somme des carrés de tous les éléments du vecteur poids. Contrairement à la régularisation L1, la régularisation L2 ne ramène pas les poids à zéro, mais contraint la complexité du modèle en ralentissant la croissance des poids. Cela résout efficacement les problèmes de colinéarité, car cela répartit le poids sur plusieurs fonctionnalités liées et évite d'être trop dépendant d'une seule fonctionnalité.
La fonction de la régularisation laplacienne est de contrôler la complexité du modèle pendant le processus de formation, évitant ainsi le surajustement. Plus la valeur du paramètre de régularisation est grande, plus l’impact du terme de pénalité sur la perte du modèle est grand et plus le modèle est complexe. Par conséquent, en ajustant la valeur du paramètre de régularisation, nous pouvons contrôler le compromis entre la complexité et la capacité de généralisation du modèle.
En bref, la régularisation laplacienne est une méthode courante de régularisation de modèle d'apprentissage automatique. Elle limite la complexité du modèle en ajoutant un terme de pénalité L1 ou L2 à la fonction de perte, évitant ainsi le surajustement et améliorant la capacité de généralisation du modèle. Dans les applications pratiques, nous devons effectuer une sélection basée sur les caractéristiques de l'ensemble de données et les performances du modèle, et trouver le degré de régularisation optimal en ajustant la valeur du paramètre de régularisation.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 L'écart de compétences en IA ralentit les chaînes d'approvisionnementApr 26, 2025 am 11:13 AM
L'écart de compétences en IA ralentit les chaînes d'approvisionnementApr 26, 2025 am 11:13 AMLe terme «main-d'œuvre prêt pour l'IA» est fréquemment utilisé, mais qu'est-ce que cela signifie vraiment dans l'industrie de la chaîne d'approvisionnement? Selon Abe Eshkenazi, PDG de l'Association for Supply Chain Management (ASCM), il signifie des professionnels capables de critique
 Comment une entreprise travaille tranquillement pour transformer l'IA pour toujoursApr 26, 2025 am 11:12 AM
Comment une entreprise travaille tranquillement pour transformer l'IA pour toujoursApr 26, 2025 am 11:12 AMLa révolution de l'IA décentralisée prend tranquillement de l'ampleur. Ce vendredi à Austin, au Texas, le Sommet de fin de partie Bittensor marque un moment pivot, en transition de l'IA décentralisée (DEAI) de la théorie à l'application pratique. Contrairement à la publicité fastueuse
 NVIDIA publie des microservices NEMO pour rationaliser le développement des agents AIApr 26, 2025 am 11:11 AM
NVIDIA publie des microservices NEMO pour rationaliser le développement des agents AIApr 26, 2025 am 11:11 AML'IA de l'entreprise fait face à des défis d'intégration des données L'application de l'IA de l'entreprise est confrontée à un défi majeur: la construction de systèmes qui peuvent maintenir la précision et la pratique en apprenant continuellement les données commerciales. Les microservices NEMO résolvent ce problème en créant ce que NVIDIA décrit comme "Data Flywheel", permettant aux systèmes d'IA de rester pertinents par une exposition continue aux informations de l'entreprise et à l'interaction des utilisateurs. Cette boîte à outils nouvellement lancée contient cinq microservices clés: NEMO Customizer gère le réglage fin des modèles de grands langues avec un débit de formation plus élevé. L'évaluateur NEMO fournit une évaluation simplifiée des modèles d'IA pour les repères personnalisés. NEMO Guar-Rails met en œuvre des contrôles de sécurité pour maintenir la conformité et la pertinence
 L'IA dépeint une nouvelle image pour l'avenir de l'art et du designApr 26, 2025 am 11:10 AM
L'IA dépeint une nouvelle image pour l'avenir de l'art et du designApr 26, 2025 am 11:10 AMAI: L'avenir de l'art et du design L'intelligence artificielle (IA) modifie le domaine de l'art et de la conception de manière sans précédent, et son impact ne se limite plus aux amateurs, mais affectant plus profondément les professionnels. Les schémas d'œuvres d'art et de conception générés par l'IA remplacent rapidement les images et les concepteurs de matériaux traditionnels dans de nombreuses activités de conception transactionnelles telles que la publicité, la génération d'images des médias sociaux et la conception Web. Cependant, les artistes et designers professionnels trouvent également la valeur pratique de l'IA. Ils utilisent l'IA comme outil auxiliaire pour explorer de nouvelles possibilités esthétiques, mélanger différents styles et créer de nouveaux effets visuels. L'IA aide les artistes et les concepteurs à automatiser les tâches répétitives, à proposer différents éléments de conception et à fournir une contribution créative. L'IA prend en charge le transfert de style, qui doit appliquer un style d'image
 Comment le zoom révolutionne le travail avec l'agent AI: des réunions aux jalonsApr 26, 2025 am 11:09 AM
Comment le zoom révolutionne le travail avec l'agent AI: des réunions aux jalonsApr 26, 2025 am 11:09 AMZoom, initialement connu pour sa plate-forme de vidéoconférence, dirige une révolution en milieu de travail avec son utilisation innovante de l'IA agentique. Une conversation récente avec le CTO de Zoom, XD Huang, a révélé la vision ambitieuse de l'entreprise. Définition de l'IA agentique Huang D
 La menace existentielle pour les universitésApr 26, 2025 am 11:08 AM
La menace existentielle pour les universitésApr 26, 2025 am 11:08 AML'IA va-t-elle révolutionner l'éducation? Cette question provoque une réflexion sérieuse entre les éducateurs et les parties prenantes. L'intégration de l'IA dans l'éducation présente à la fois des opportunités et des défis. Comme le note Matthew Lynch de The Tech Edvocate, Universit
 Le prototype: les scientifiques américains recherchent des emplois à l'étrangerApr 26, 2025 am 11:07 AM
Le prototype: les scientifiques américains recherchent des emplois à l'étrangerApr 26, 2025 am 11:07 AMLe développement de la recherche scientifique et de la technologie aux États-Unis peut faire face à des défis, peut-être en raison de coupes budgétaires. Selon la nature, le nombre de scientifiques américains postulant pour des emplois à l'étranger a augmenté de 32% de janvier à mars 2025 par rapport à la même période en 2024. Un sondage précédent a montré que 75% des chercheurs interrogés envisageaient de rechercher des emplois en Europe et au Canada. Des centaines de subventions NIH et NSF ont été licenciées au cours des derniers mois, avec les nouvelles subventions du NIH d'environ 2,3 milliards de dollars cette année, une baisse de près d'un tiers. Le projet de budget divulgué montre que l'administration Trump envisage de réduire fortement les budgets pour les institutions scientifiques, avec une réduction possible allant jusqu'à 50%. La tourmente dans le domaine de la recherche fondamentale a également affecté l'un des principaux avantages des États-Unis: attirer des talents à l'étranger. 35
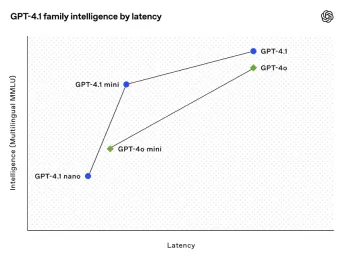 Tout sur la dernière famille GPT 4.1 d'Open AI - Analytics VidhyaApr 26, 2025 am 10:19 AM
Tout sur la dernière famille GPT 4.1 d'Open AI - Analytics VidhyaApr 26, 2025 am 10:19 AMOpenAI dévoile la puissante série GPT-4.1: une famille de trois modèles de langage avancé conçus pour des applications réelles. Ce saut significatif en avant offre des temps de réponse plus rapides, une compréhension améliorée et des coûts considérablement réduits par rapport à T


Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version anglaise
Recommandé : version Win, prend en charge les invites de code !

mPDF
mPDF est une bibliothèque PHP qui peut générer des fichiers PDF à partir de HTML encodé en UTF-8. L'auteur original, Ian Back, a écrit mPDF pour générer des fichiers PDF « à la volée » depuis son site Web et gérer différentes langues. Il est plus lent et produit des fichiers plus volumineux lors de l'utilisation de polices Unicode que les scripts originaux comme HTML2FPDF, mais prend en charge les styles CSS, etc. et présente de nombreuses améliorations. Prend en charge presque toutes les langues, y compris RTL (arabe et hébreu) et CJK (chinois, japonais et coréen). Prend en charge les éléments imbriqués au niveau du bloc (tels que P, DIV),

Version crackée d'EditPlus en chinois
Petite taille, coloration syntaxique, ne prend pas en charge la fonction d'invite de code

Adaptateur de serveur SAP NetWeaver pour Eclipse
Intégrez Eclipse au serveur d'applications SAP NetWeaver.






