Méthode d'implémentation Matlab et affichage graphique de solutions numériques et analytiques au problème de valeur initiale d'équations différentielles dans un intervalle

Utilisez Matlab pour résoudre le problème de la valeur initiale des équations différentielles. La solution numérique et la plage de solutions analytiques sont des intervalles et dessinées .

Utilisez Matlab pour résoudre l'équation différentielle 5261, solution numérique, problème de valeur initiale 4102 et solution analytique, vous pouvez le gérer comme ceci :

1.Solution numérique

La solution numérique au problème de la valeur initiale des équations différentielles peut être résolue à l'aide de la fonction ode.

Tout d'abord, personnalisez la fonction de l'équation différentielle, c'est-à-dire

dy = 3/x*y+x^3*(exp(x)+cos(x))-2*x;

Deuxièmement, déterminez les conditions initiales, c'est-à-dire

y0=[(exp(pi)+2/pi)*pi^3];

Troisièmement, utilisez la fonction ode45 pour trouver sa solution numérique [x, y]

2.Solution analytique

La solution analytique du problème de la valeur initiale des équations différentielles peut être résolue à l'aide de la fonction dsolve.

Tout d'abord, déclarez une variable pour y(x), c'est-à-dire

syms y(x)

Deuxièmement, la dérivée première de y(x), qui est

Dy=diff(y,1)

Troisièmement, utilisez la fonction dsolve pour trouver l'expression de sa solution analytique y(x)

y=dsolve(Dy==3/x*y+x^3*(exp(x)+cos(x))-2*x,y(pi)==(exp(pi)+2/pi) *pi^3)

3. Dessinez des courbes de solution numérique et de solution analytique

Tout d'abord, utilisez la fonction plot pour tracer la courbe de la solution numérique

intrigue (x.y)

Deuxièmement, calculez la valeur y qui est équivalente à y pour une série de valeurs de x dans l'intervalle [π, 2π]

Troisièmement, utilisez la fonction plot pour tracer la courbe de la solution analytique

Après avoir exécuté le code, vous pouvez obtenir les résultats suivants.

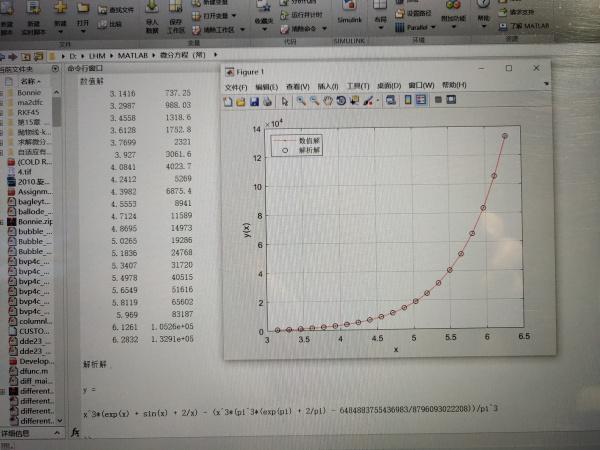
problème Matlab

%%%%%%%%%%%%%%%%%%%% programme source

i=0;equ=0;sum=0;

data=input('veuillez saisir le numéro : ');

pendant(données~=0)

somme=somme+données;

key=input('veuillez continuer : ');

data=clé;

i=i+1;

fin

equ=somme/i;

equ,sum

%%%%%%%%%%%%%%%%%%%%%%%%%

Résultat de l'exécution :

veuillez saisir le numéro : 1

continuez s'il vous plaît : 2

continuez s'il vous plaît : 3

continuez s'il vous plaît : 4

continuez s'il vous plaît : 5

continuez s'il vous plaît : 0

equ =

3

somme =

15

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!