Logique de code pour implémenter un algorithme de descente de gradient par mini-lots à l'aide de Python

Soit theta = paramètres du modèle et max_iters = nombre d'époques. Pour itr=1,2,3,...,max_iters : Pour mini_batch(X_mini,y_mini) :

Passage direct du lot X_mini :

1 Prédisez le mini-lot

2. des paramètres Calculer l'erreur de prédiction (J(theta))

Post-transmission : Calculer le gradient (theta)=J(theta) par rapport à la dérivée partielle de theta

Mettre à jour les paramètres : theta=theta–learning_rate*gradient(theta )

Python implémente le flux de code de l'algorithme de descente de gradient

Étape 1 : importez les dépendances, générez des données pour la régression linéaire et visualisez les données générées. Prenez 8 000 exemples de données, chaque exemple possède 2 caractéristiques d'attribut. Ces échantillons de données sont ensuite divisés en ensemble d'apprentissage (X_train, y_train) et ensemble de test (X_test, y_test), avec respectivement 7 200 et 800 échantillons.

import numpy as np
import matplotlib.pyplot as plt

mean=np.array([5.0,6.0])
cov=np.array([[1.0,0.95],[0.95,1.2]])
data=np.random.multivariate_normal(mean,cov,8000)

plt.scatter(data[:500,0],data[:500,1],marker='.')
plt.show()
data=np.hstack((np.ones((data.shape[0],1)),data))
split_factor=0.90
split=int(split_factor*data.shape[0])
X_train=data[:split,:-1]
y_train=data[:split,-1].reshape((-1,1))
X_test=data[split:,:-1]
y_test=data[split:,-1].reshape((-1,1))

print(& quot Number of examples in training set= % d & quot % (X_train.shape[0]))
print(& quot Number of examples in testing set= % d & quot % (X_test.shape[0]))

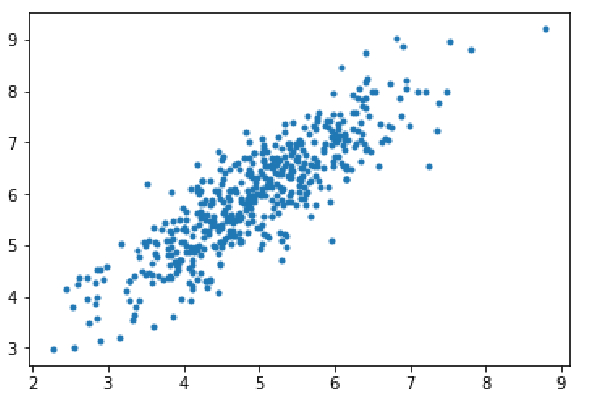
Nombre d'exemples dans l'ensemble d'entraînement = 7200 Nombre d'exemples dans l'ensemble de test = 800

Étape 2 :

Code pour implémenter la régression linéaire en utilisant la descente de gradient par mini-lots. gradientDescent() est la fonction motrice principale, et d'autres fonctions sont des fonctions auxiliaires :

Faire des prédictions - hypothese()

Calculer le dégradé - gradient()

Calculer l'erreur - cost()

Créer des mini lots - create_mini_batches ( )

La fonction pilote initialise les paramètres, calcule l'ensemble optimal de paramètres pour le modèle et renvoie ces paramètres ainsi qu'une liste contenant l'historique des erreurs au fur et à mesure de la mise à jour des paramètres.

def hypothesis(X,theta):
    return np.dot(X,theta)

def gradient(X,y,theta):
    h=hypothesis(X,theta)
    grad=np.dot(X.transpose(),(h-y))
    return grad

def cost(X,y,theta):
    h=hypothesis(X,theta)
    J=np.dot((h-y).transpose(),(h-y))
    J/=2
    return J[0]

def create_mini_batches(X,y,batch_size):
    mini_batches=[]
    data=np.hstack((X,y))
    np.random.shuffle(data)
    n_minibatches=data.shape[0]//batch_size
    i=0
    for i in range(n_minibatches+1):
        mini_batch=data[i*batch_size:(i+1)*batch_size,:]
        X_mini=mini_batch[:,:-1]
        Y_mini=mini_batch[:,-1].reshape((-1,1))
        mini_batches.append((X_mini,Y_mini))
    if data.shape[0]%batch_size!=0:
       mini_batch=data[i*batch_size:data.shape[0]]
       X_mini=mini_batch[:,:-1]
       Y_mini=mini_batch[:,-1].reshape((-1,1))
       mini_batches.append((X_mini,Y_mini))
    return mini_batches

def gradientDescent(X,y,learning_rate=0.001,batch_size=32):
    theta=np.zeros((X.shape[1],1))
    error_list=[]
    max_iters=3
    for itr in range(max_iters):
        mini_batches=create_mini_batches(X,y,batch_size)
        for mini_batch in mini_batches:
            X_mini,y_mini=mini_batch
            theta=theta-learning_rate*gradient(X_mini,y_mini,theta)
            error_list.append(cost(X_mini,y_mini,theta))
    return theta,error_list

Appelez la fonction gradientDescent() pour calculer les paramètres du modèle (thêta) et visualiser les changements dans la fonction d'erreur.

theta,error_list=gradientDescent(X_train,y_train)
print("Bias=",theta[0])
print("Coefficients=",theta[1:])

plt.plot(error_list)
plt.xlabel("Number of iterations")
plt.ylabel("Cost")
plt.show()

Deviation=[0.81830471]Coefficient=[[1.04586595]]

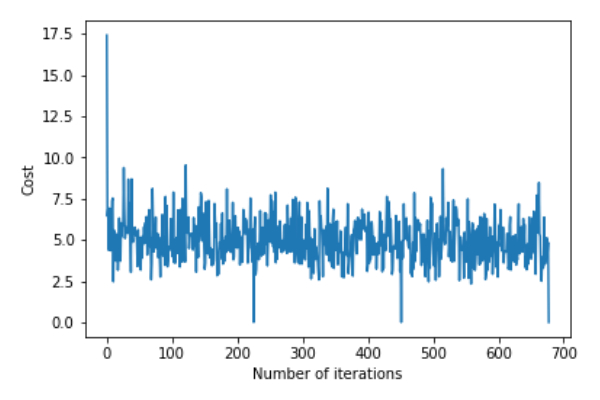
Étape 3 : Prédisez l'ensemble de test et calculez l'erreur absolue moyenne dans la prédiction.

y_pred=hypothesis(X_test,theta)
plt.scatter(X_test[:,1],y_test[:,],marker='.')
plt.plot(X_test[:,1],y_pred,color='orange')
plt.show()

error=np.sum(np.abs(y_test-y_pred)/y_test.shape[0])
print(& quot Mean absolute error=&quot,error)

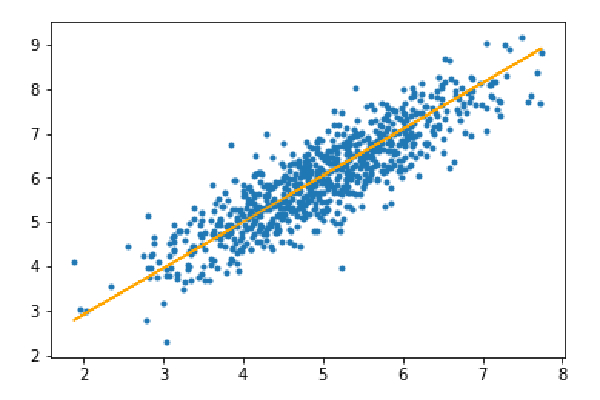
Erreur absolue moyenne=0,4366644295854125

La ligne orange représente la fonction d'hypothèse finale : theta[0]+theta[1]*X_test[:,1]+theta[2]*X_test[:,2]=0

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!