Google Mathematical AI publie un article dans Nature : Proving Beyond Wu Wenjun's 1978 Law Theorem, démontrant un niveau géométrique de classe mondiale

Google DeepMind publie à nouveau Nature, l'IA de la série Alpha revient et le niveau de mathématiques s'améliore à pas de géant.

AlphaGeometry, pas besoin de démonstration humaine pour atteindre le niveau de géométrie des joueurs médaillés d'or de l'OMI.

C'est comme quand AlphaZero apprenait le Go sans connaissance humaine "Maîtriser le jeu de Go sans connaissance humaine".

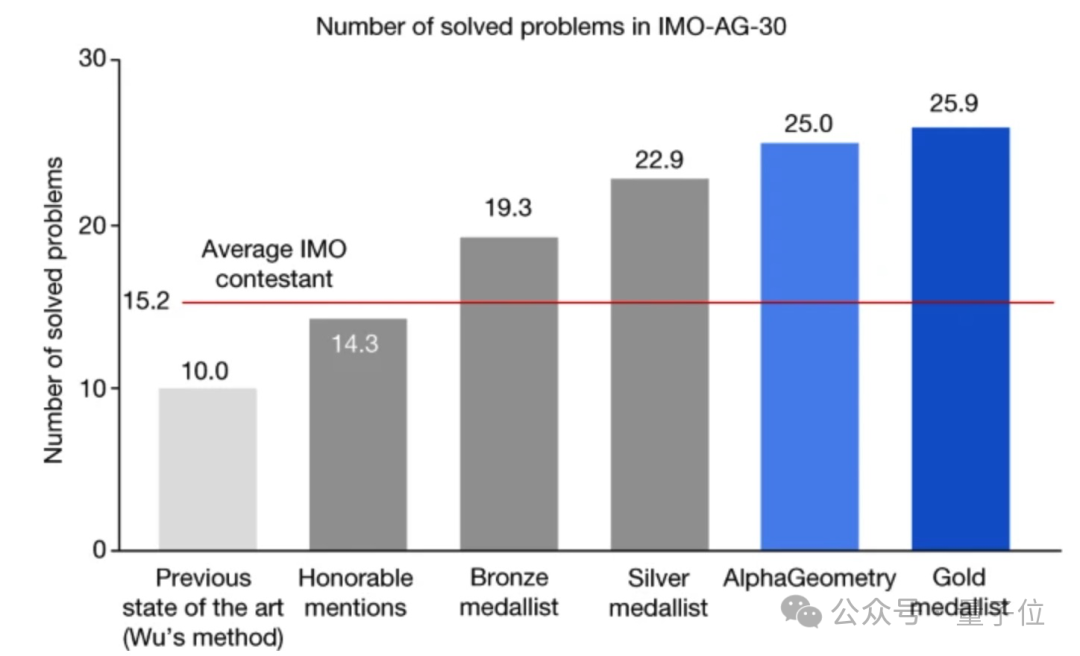
AlphaGeometry a obtenu 25 des 30 théorèmes géométriques de difficulté de l'OMI prouvant que les questions sont correctes, tandis que le joueur médaillé d'or humain moyen a obtenu 25,9 correctement. De plus, la méthode SOTA précédente (méthode Wu Wenjun en 1978) ne pouvait obtenir que 10 bonnes réponses.

Médaillé d'or de l'IMO Evan Chen(Evan Chen) était chargé d'évaluer les réponses générées par l'IA. Il a commenté :

Le résultat d'AlphaGeometry est impressionnant, à la fois fiable et propre. Les solutions d’IA précédentes ont été aléatoires, ce qui a donné lieu à des résultats qui nécessitaient parfois une révision manuelle.

Les solutions d'AlphaGeometry ont une structure vérifiable qui peut être vérifiée à la fois par les machines et comprise par les humains. Il utilise les règles de géométrie classiques comme les angles et les triangles similaires, tout comme les étudiants.

En plus des résultats exceptionnels, trois points clés de cette étude ont attiré l'attention de l'industrie :

• Aucune démonstration humaine n'est requise, c'est-à-dire que seule la formation des données synthétiques de l'IA est utilisée. , poursuivant la méthode d'auto-apprentissage Go d'AlphaZero.
• Grand modèle combiné avec d'autres méthodes d'IA, similaire aux rumeurs AlphaGo et OpenAI Q*.
• Contrairement à de nombreuses méthodes précédentes, AlphaGeometry peut générer des processus de preuve lisibles par l'homme, et le modèle et le code sont open source.

L'équipe estime qu'AlphaGeometry fournit un cadre potentiel pour atteindre des capacités de raisonnement avancées et découvrir de nouvelles connaissances.

Cela pourrait contribuer à faire progresser la démonstration de théorèmes en intelligence artificielle, considérée comme une étape clé dans la construction de l'AGI.

De plus, lors du processus de communication avec l'équipe de l'auteur, Qubits a demandé si AlphaGeometry serait réellement autorisé à participer à une compétition IMO, tout comme AlphaGo a défié le champion humain de Go.

Ils ont déclaré qu'ils travaillaient dur pour améliorer les capacités du système et qu'ils devaient également permettre à l'IA de résoudre un plus large éventail de problèmes mathématiques au-delà de la géométrie.

L'IA prouve que la géométrie dessine également des lignes auxiliaires

Auparavant, le système d'IA ne pouvait pas bien résoudre les problèmes géométriques et il était bloqué en raison du manque de données d'entraînement de haute qualité.

Les humains qui apprennent la géométrie peuvent utiliser les connaissances existantes sur les images pour découvrir des propriétés et des relations géométriques nouvelles et plus complexes à l'aide de papier et d'un stylo.

À cette fin, l'équipe de Google a généré 1 milliard de graphiques d'objets géométriques aléatoires, ainsi que toutes les relations entre leurs points et leurs lignes, et a finalement filtré 100 millions de théorèmes uniques et de preuves de différentes difficultés. AlphaGeometry a été entièrement formé à partir de zéro. ces données.

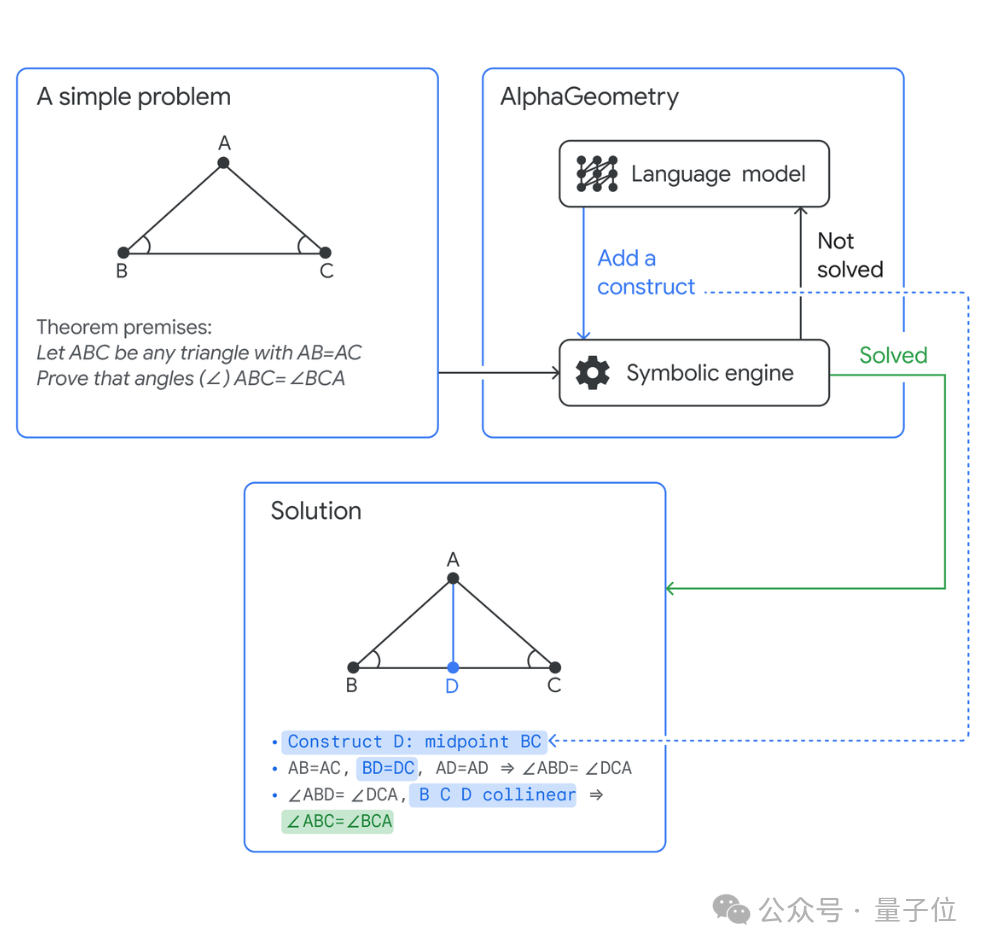
Le système se compose de deux modules qui fonctionnent ensemble pour trouver des preuves géométriques complexes.

• Modèle de langage, prédisant la géométrie qui peut être utilisée pour résoudre le problème (c'est-à-dire ajouter des lignes auxiliaires) .
• Moteur de raisonnement symbolique, utilisant des règles logiques pour tirer des conclusions.

Le premier auteur, Trieu Trinh, a expliqué que le processus de fonctionnement de l'AlphaGeometry est similaire à la façon dont le cerveau humain est divisé en deux types : rapide et lent.

C'est le concept de « Système 1, Système 2 » popularisé dans le livre à succès du prix Nobel Daniel Kahneman « Penser vite et lentement ».

Le système 1 fournit des idées rapides et intuitives, tandis que le système 2 fournit des décisions plus réfléchies et rationnelles.

D'une part, les modèles de langage sont efficaces pour identifier des modèles et des relations dans les données et peuvent rapidement prédire des structures auxiliaires potentiellement utiles, mais n'ont souvent pas la capacité de raisonner ou d'expliquer rigoureusement leurs décisions.

D'autre part, les moteurs de raisonnement symbolique sont basés sur une logique formelle et utilisent des règles explicites pour tirer des conclusions. Ils sont rationnels et explicables, mais ils sont lents et inflexibles, surtout lorsqu’ils traitent seuls de problèmes importants et complexes.

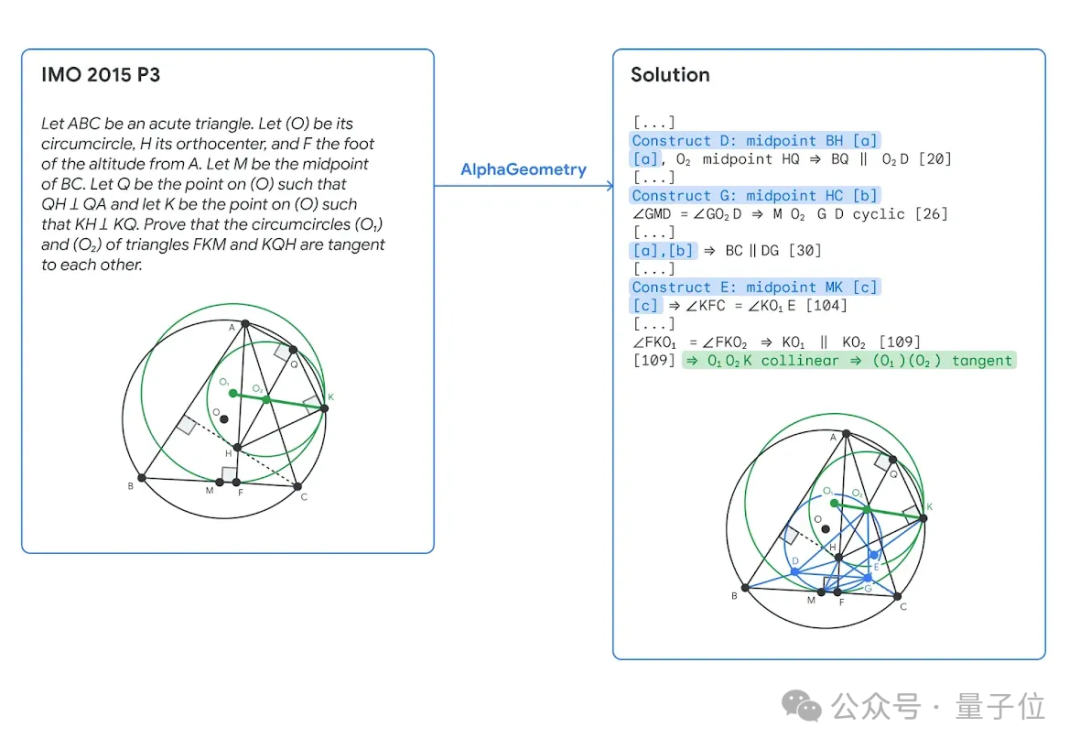
Par exemple, lors de la résolution d'une question du concours IMO 2015, la partie bleue est la structure auxiliaire ajoutée par le modèle de langage d'AlphaGeometry, et la partie verte est la version simplifiée de la preuve finale, avec un total de 109 étapes.

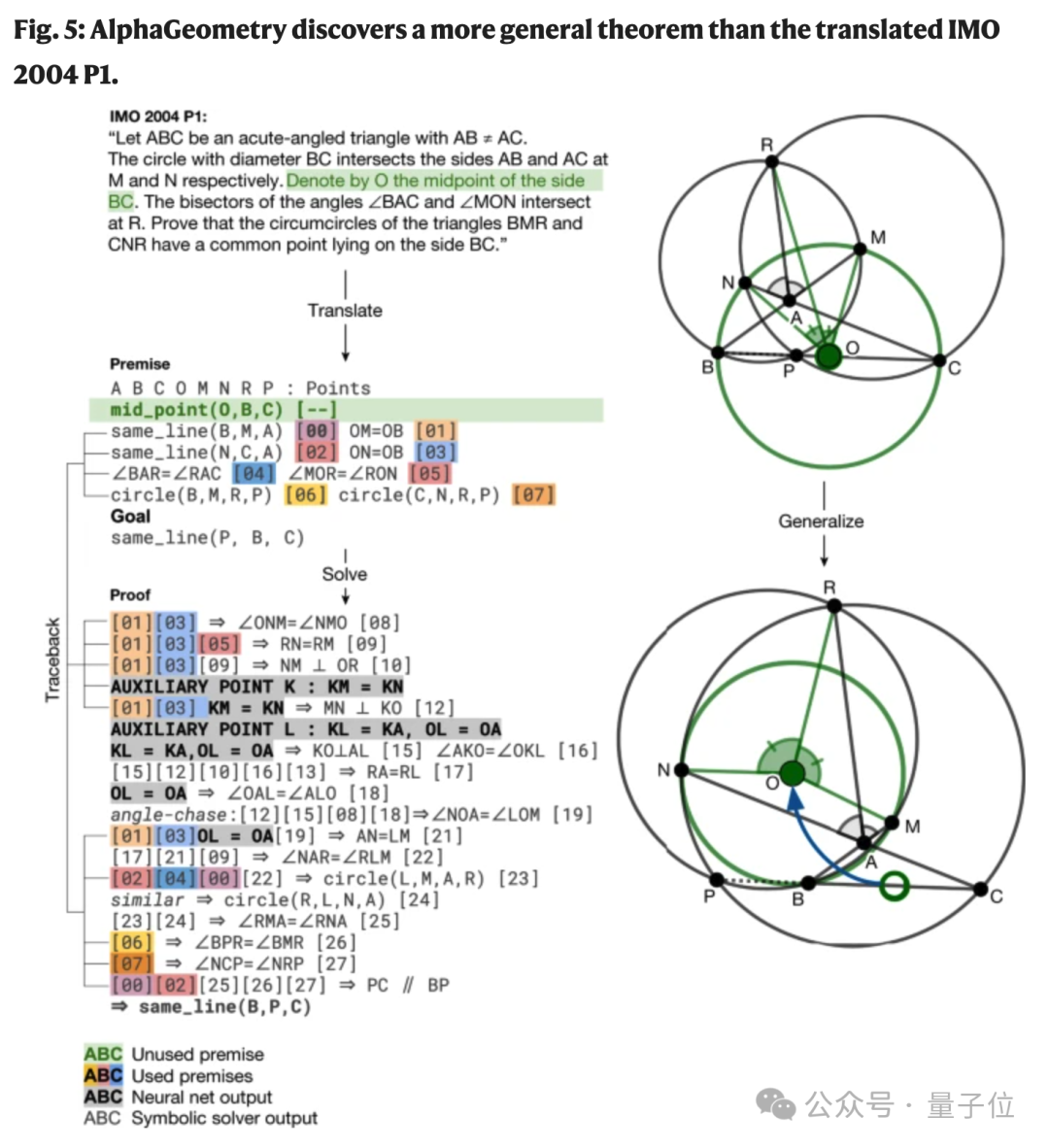
Au cours du processus de résolution du problème, AlphaGeometry a également découvert une condition préalable inutilisée dans le problème de compétition de l'OMI de 2004, et a ainsi découvert une version plus large du théorème.

On peut prouver que P, B et C sont colinéaires sans la condition que O soit le milieu de BC.

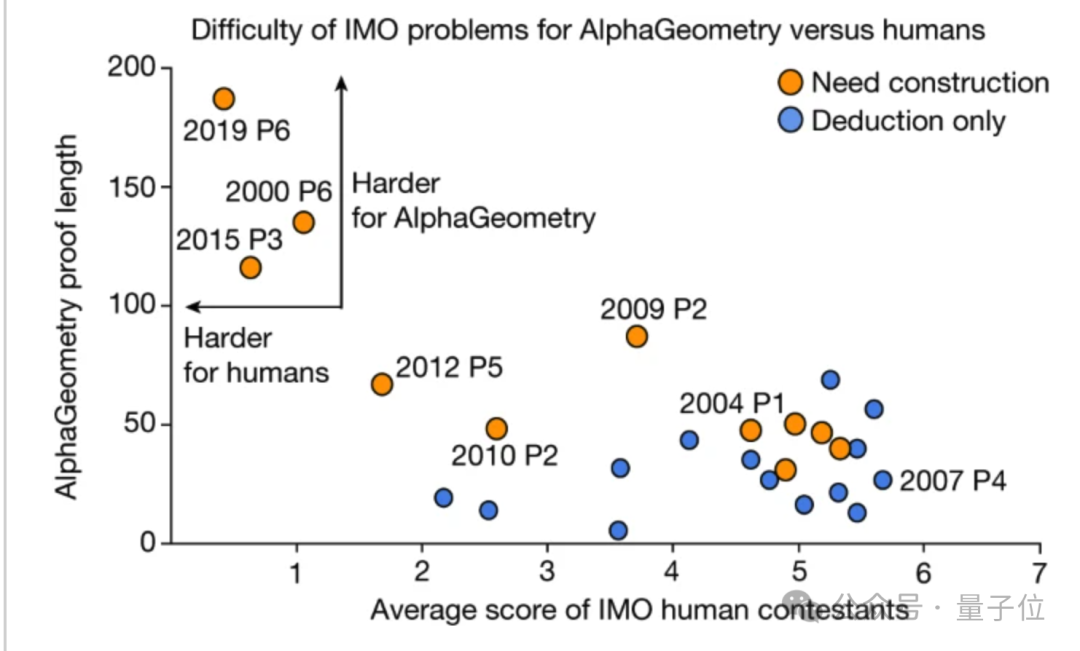
De plus, la recherche a également révélé que pour les trois problèmes avec les scores humains les plus bas, AlphaGeometry nécessite également un très long processus de preuve et l'ajout de nombreuses structures auxiliaires à résoudre.

Mais sur les questions relativement faciles, il n'y avait pas de corrélation significative entre le score humain moyen et la longueur des preuves générées par l'IA (p = −0,06).

One More Thing

Concernant la connexion et la différence entre AlphaGeometry et AlphaGo, lors du processus de communication avec l'équipe, le scientifique de Google Quoc Le a présenté :

Ils sont tous les deux dans une décision très complexe- faire de l'espace Recherche, mais la méthode d'AlphaGo est plus traditionnelle (Remarque : le réseau neuronal est responsable de la reconnaissance des formes) Le réseau neuronal d'AlphaGeometry est chargé de suggérer la prochaine action à entreprendre et de guider l'algorithme de recherche pour qu'il se déplace dans la bonne direction. dans l’espace de décision.

Bien que ce résultat porte le nom de la série Alpha et que la première unité soit également Google DeepMind, l'auteur est en fait un ancien membre de Google Brain.

Maître Quoc Le n'a pas besoin d'être présenté. Le premier auteur Trieu Trinh et l'auteur correspondant Thang Luong ont tous deux travaillé chez Google pendant six ou sept ans. Thang Luong lui-même était également un joueur de l'OMI au lycée.

Parmi les deux auteurs chinois, He He est professeur assistant à l'Université de New York. Wu Yuhuai a déjà participé à la recherche du grand modèle mathématique Minerva de Google et a maintenant quitté Google pour rejoindre l'équipe de Musk et devenir l'un des co-fondateurs de xAI.

Adresse papier : https://www.nature.com/articles/s41586-023-06747-5.

Lien de référence :
[1]https://www.nature.com/articles/d4186-024-00141-5.

[2]https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!