L'apprentissage profond atteint des performances de génie en raisonnement géométrique. Nature publie le modèle de DeepMind et reçoit des éloges dans l'actualité des lauréats de la médaille Fields.

Ce travail représente une percée dans les capacités de raisonnement mathématique de l’IA et constitue une étape importante dans le développement de systèmes généraux d’IA.

Cette fois, l'algorithme d'intelligence artificielle a réalisé une percée majeure lors de l'Olympiade de mathématiques (OMI).

Dans le dernier numéro de la revue de renommée internationale "Nature", un article a été publié présentant un système d'intelligence artificielle appelé AlphaGeometry. Le système est capable de résoudre les problèmes de géométrie olympique sans démonstration humaine. Les experts estiment qu'il s'agit d'une étape importante dans les progrès de l'intelligence artificielle vers la possession de capacités de raisonnement humain. La publication de ces résultats de recherche revêt une grande importance pour promouvoir le développement ultérieur de l’intelligence artificielle.

Lien de l'article : https://www.nature.com/articles/s41586-023-06747-5

DeepMind a également rendu le code et le modèle open source dès la publication de l'article, GitHub : https : // github.com/google-deepmind/alphageometry

Il s'agit d'un système d'intelligence artificielle des chercheurs de Google DeepMind, qui peut résoudre des problèmes géométriques complexes à un niveau proche de celui des médaillés d'or des Olympiades humaines.

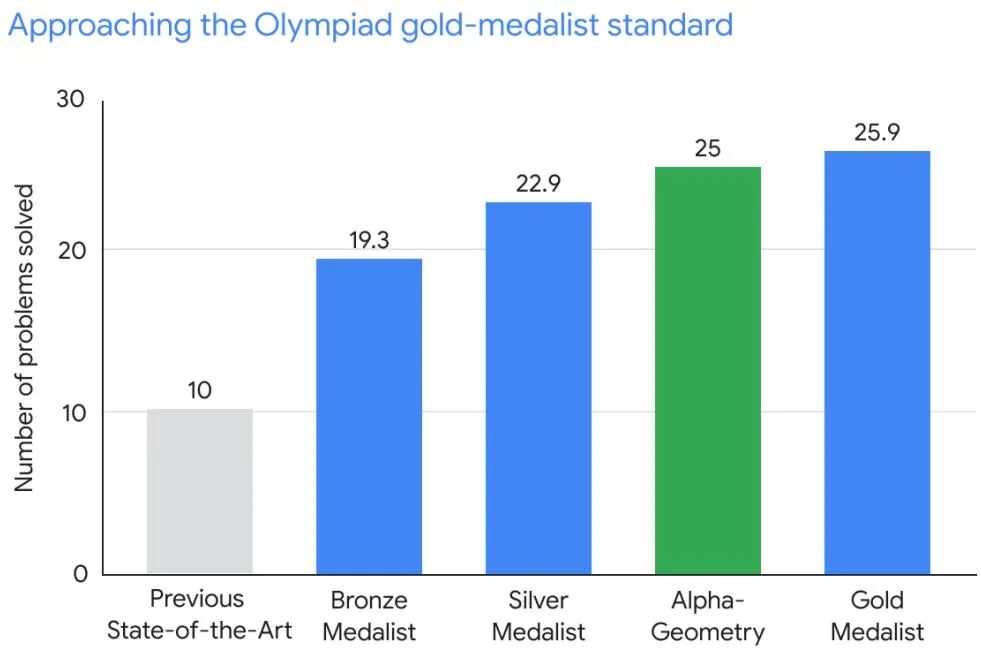
Dans un test de référence de 30 questions de géométrie de l'Olympiade mathématique, AlphaGeometry a résolu 25 des questions de géométrie dans le délai standard de l'Olympiade mathématique, alors que le système de pointe précédent n'a résolu que 10 des questions de géométrie. À titre de comparaison, les médaillés d’or humains ont résolu en moyenne 25,9 problèmes.

La preuve de théorèmes est une tâche difficile pour les modèles d'IA basés sur l'apprentissage. La raison principale est que les preuves humaines dans la plupart des domaines mathématiques sont difficiles à traduire dans un langage vérifiable par machine, limitant ainsi la quantité de données utilisées pour entraîner les modèles d’IA. Pour surmonter ce problème, DeepMind propose une méthode alternative d'utilisation de données synthétiques pour la preuve de théorèmes. Ils ont développé un cadre d’orientation général appelé AlphaGeometry qui est applicable dans de nombreux domaines. En exploitant des données synthétiques, AlphaGeometry est capable de former des modèles d'IA pour la preuve de théorèmes et de produire des résultats de haute qualité. Cette méthode apporte une solution efficace à la difficulté de la démonstration des théorèmes.

Introduction à la recherche

AlphaGeometry combine des modèles de langage avec des « moteurs symboliques » pour effectuer des inférences mathématiques à l'aide de symboles et de règles logiques. Parmi eux, le modèle de langage est efficace pour identifier et prédire les étapes ultérieures du processus, mais manque de la rigueur requise pour le raisonnement mathématique ; en revanche, le moteur symbolique est purement basé sur une logique formelle et des règles strictes, qui lui permet d’orienter le modèle linguistique vers une prise de décision rationnelle.

Dans le cadre de la recherche sur AlphaGeometry, DeepMind a effectué des tests à partir de l'ensemble de tests de référence de 30 problèmes de géométrie olympique (IMO-AG-30) s'étalant de 2000 à 2022. Les résultats ont montré qu'AlphaGeometry peut résoudre le problème dans le délai de compétition de 25 questions. . La méthode de pointe précédente (méthode de Wu) ne pouvait en résoudre que 10.

Il est bien connu que les systèmes d’IA ont souvent du mal à résoudre des problèmes complexes de géométrie et de mathématiques en raison d’un manque de capacités de raisonnement et de données d’entraînement. Le système AlphaGeometry combine la puissance prédictive des modèles de langage neuronal avec un moteur d'inférence contraint par des règles, qui travaillent ensemble pour trouver de nouvelles solutions.

De plus, pour relever le défi des données, l'étude a généré une grande quantité de données d'entraînement synthétiques, soit 100 millions d'exemples, dans lesquels les preuves de nombreux théorèmes nécessitent plus de 200 étapes, soit 4 fois plus longues que la durée moyenne de preuve de Théorèmes de l'Olympiade mathématique.

AlphaGeometry démontre les capacités croissantes de raisonnement logique de l’IA et sa capacité à découvrir et vérifier de nouvelles connaissances. La résolution de problèmes de géométrie de niveau olympique constitue une étape importante pour l’IA sur la voie de systèmes d’intelligence artificielle plus avancés et plus généraux.

Ngô Bảo Châu, lauréat de la médaille Fields et médaillé d'or de l'OMI, a déclaré : « Maintenant, je comprends parfaitement pourquoi les chercheurs en IA tentent d'abord de résoudre les problèmes de géométrie de l'Olympiade mathématique internationale (OMI), car les trouver. La solution, c'est un peu comme jouer aux échecs, nous avons relativement peu de mouvements raisonnables à chaque mouvement, mais je suis toujours choqué qu'ils aient pu réussir cela

^{Wu Baozhu, lauréat de la médaille Fields 2010, est actuellement professeur à l'Université de. Chicago.}

AlphaGeometry est un système neuro-symbolique composé d'un modèle de langage neuronal et d'un moteur de déduction symbolique qui travaillent ensemble pour trouver des preuves de théorèmes géométriques complexes. Un système fournit des idées rapides et intuitives, tandis que l'autre fournit des décisions plus réfléchies et rationnelles.

Étant donné que les modèles de langage sont efficaces pour identifier les modèles généraux et les relations dans les données, ils peuvent rapidement prédire des structures potentiellement utiles, mais manquent souvent de raisonnement ou d'interprétation rigoureux. Le moteur de déduction symbolique, quant à lui, est basé sur une logique formelle et utilise des règles explicites pour parvenir à des conclusions qui, ensemble, constituent AlphaGeometry.

Le modèle de langage d'AlphaGeometry guide son moteur de déduction symbolique pour trouver des solutions possibles aux problèmes géométriques. Les problèmes de géométrie générale des Olympiades sont basés sur des diagrammes et nécessitent l'ajout de nouvelles structures géométriques à résoudre, telles que des points, des lignes ou des cercles. Le modèle de langage d'AlphaGeometry peut prédire quelles nouvelles structures seraient les plus utiles à ajouter parmi d'innombrables possibilités. Ces indices aident à combler les lacunes et permettent au moteur symbolique de faire d'autres déductions sur le diagramme et de se rapprocher d'une solution.

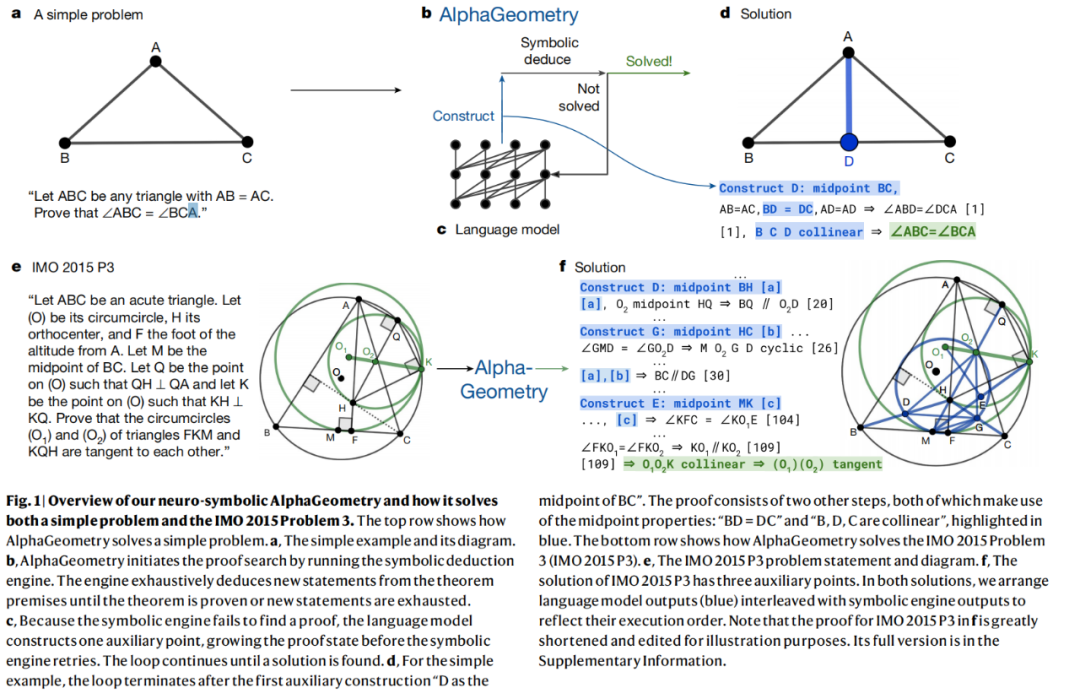
Par exemple, l'image ci-dessous (ci-dessus) montre le processus d'AlphaGeometry pour résoudre une question simple. La question est "Laissez ABC être n'importe quel triangle avec AB = AC. Prouvez que ∠ABC =

AlphaGeometry Le processus de preuve." est la suivante : AlphaGeometry Démarrez la recherche de preuves en exécutant le moteur de déduction symbolique. Ce moteur part des prémisses du théorème et dérive de manière exhaustive de nouveaux énoncés jusqu'à ce que le théorème soit prouvé ou que les nouveaux énoncés soient épuisés. Si le moteur symbolique ne parvient pas à trouver une preuve, le modèle de langage construit un point auxiliaire qui ajoute des conditions prouvables avant le redémarrage du moteur symbolique. Ce cycle continue jusqu'à ce qu'une solution soit trouvée. Pour l'exemple simple, la boucle se termine après la première structure auxiliaire "ajouter le point D au milieu de BC".

L'image ci-dessous montre la solution d'AlphaGeometry au problème de l'OMI. "Prouver que les cercles circonscrits (O1) et (O2) des triangles FKM et KQH sont tangents entre eux..." AlphaGeometry peut également prouver un problème aussi complexe, et le processus de preuve fournit également des points auxiliaires, etc. La preuve a été considérablement raccourcie et éditée à des fins d'illustration.

Génération de 100 millions de données de formation à l'inférence mathématique

Les humains peuvent apprendre la géométrie en dessinant sur papier, en examinant des diagrammes et en utilisant les connaissances existantes pour découvrir de nouvelles propriétés et relations géométriques plus complexes. L'approche de cette étude pour générer des données synthétiques simule ce processus de création de connaissances à grande échelle. La méthode de génération de données synthétiques est illustrée à la figure 3.

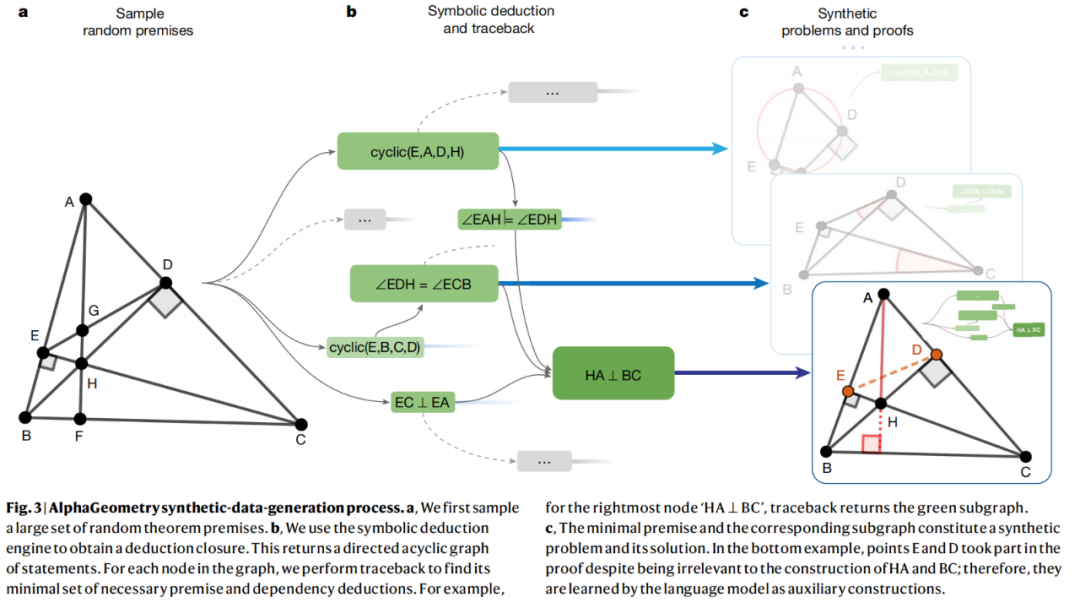
Grâce au calcul hautement parallèle, le système génère d'abord des graphiques aléatoires de 500 millions d'objets géométriques et dérive de manière exhaustive toutes les relations entre les points et les lignes de chaque graphique. AlphaGeometry trouve toutes les preuves contenues dans chaque graphique, puis travaille à rebours pour découvrir quelle structure supplémentaire, le cas échéant, est nécessaire pour obtenir ces preuves. Ce processus est « la déduction symbolique et la rétrospection ».

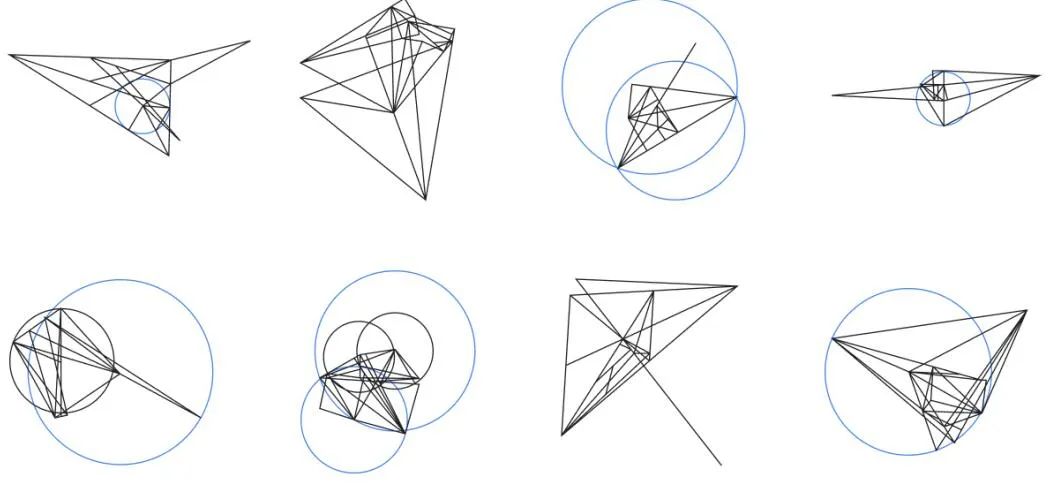
^{Représentation visuelle des données synthétiques générées par AlphaGeometry}

Ensuite, cet énorme pool de données a été filtré pour exclure des exemples similaires, ce qui a donné 100 millions d'ensembles de données d'entraînement.

Capacités pionnières de raisonnement de l'intelligence artificielle

Chaque solution fournie par AlphaGeometry a été vérifiée et vérifiée par des ordinateurs. Les chercheurs ont également comparé leurs résultats avec les précédentes méthodes d’intelligence artificielle et les performances humaines lors des compétitions olympiques. De plus, Evan Chen, coach en mathématiques et ancien médaillé d'or aux Olympiades, évalue pour nous une gamme de solutions AlphaGeometry.

^{Chen Yiting, doctorant en mathématiques au MIT, a remporté la médaille d'or de l'OMI 2014.}

Evan Chen a déclaré : « Le résultat d'AlphaGeometry est impressionnant car il est à la fois vérifiable et propre. Les solutions d'IA passées aux problèmes de concurrence fondés sur des preuves étaient parfois aléatoires (le résultat était parfois correct et nécessitait une vérification humaine), tandis que AlphaGeometry n'a pas cette faiblesse : sa solution a une structure vérifiable par machine. D'un autre côté, sa sortie est toujours lisible par l'homme. On peut imaginer un programme informatique qui résout des problèmes géométriques grâce à des systèmes de coordonnées par force brute : pensez aux pages. et des pages de calculs algébriques fastidieux, AlphaGeometry ne fait pas ça, il utilise des règles de géométrie classiques avec des angles et des triangles similaires comme le ferait un étudiant humain."

Récemment, la société de technologie financière XTX Markets a créé l'Olympiade mathématique de l'intelligence artificielle (prix AI-MO) pour encourager le développement de modèles d'intelligence artificielle capables d'effectuer un raisonnement mathématique. Étant donné que chaque Olympiade comporte six problèmes, dont seulement deux portent généralement sur la géométrie, l'AlphaGeometry ne peut être appliquée qu'à un tiers des problèmes d'une Olympiade donnée.

Malgré cela, AlphaGeometry est devenu le premier modèle d'intelligence artificielle au monde à franchir le seuil de la médaille de bronze de l'OMI en 2000 et 2015, en s'appuyant uniquement sur ses capacités de résolution de problèmes géométriques.

DeepMind travaille déjà à faire progresser l'inférence pour les systèmes d'intelligence artificielle de nouvelle génération. Les chercheurs pensent qu’étant donné le large potentiel d’utilisation de données synthétiques à grande échelle pour former des systèmes d’IA à partir de zéro, cette approche pourrait influencer la direction dans laquelle les futurs systèmes d’IA découvriront de nouvelles connaissances en mathématiques et dans d’autres domaines.

AlphaGeometry est un pionnier du raisonnement mathématique dans l'intelligence artificielle - de l'exploration de la beauté des mathématiques pures à l'utilisation de modèles de langage pour résoudre des problèmes mathématiques et scientifiques. On espère que cette technologie continuera à s’améliorer pour résoudre des problèmes mathématiques plus avancés et plus abstraits.

En plus des mathématiques, l'impact d'AlphaGeometry peut également couvrir davantage de domaines, notamment les problèmes géométriques, tels que la vision par ordinateur, l'architecture et même la physique théorique.

^{Contenu de référence :}

^{https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry/}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!