Pourquoi le Gaussian Splatting est-il si populaire dans la conduite autonome que le NeRF commence à être abandonné ?

Écrit avant et compréhension personnelle de l'auteur

Les éclaboussures gaussiennes tridimensionnelles (3DGS) sont une technologie révolutionnaire qui a émergé dans les domaines des champs de rayonnement explicites et de l'infographie ces dernières années. Cette méthode innovante se caractérise par l’utilisation de millions de gaussiennes 3D, ce qui est très différent de la méthode du champ de rayonnement neuronal (NeRF), qui utilise principalement un modèle implicite basé sur les coordonnées pour mapper les coordonnées spatiales aux valeurs des pixels. Avec sa représentation explicite des scènes et ses algorithmes de rendu différenciables, 3D GS garantit non seulement des capacités de rendu en temps réel, mais introduit également un niveau sans précédent de contrôle et d'édition de scènes. Cela positionne 3D GS comme un révolutionnaire potentiel pour la reconstruction et la représentation 3D de nouvelle génération. À cette fin, nous fournissons le premier aperçu systématique des derniers développements et des contributions clés dans le domaine du 3D GS. Tout d’abord, les principes et formules de base pour l’émergence de 3D GS sont explorés en détail, jetant les bases pour comprendre sa signification. Ensuite, le côté pratique de 3D GS est discuté en profondeur. En facilitant les performances en temps réel, 3D GS ouvre une multitude d'applications, de la réalité virtuelle aux médias interactifs et bien plus encore. De plus, une analyse comparative des principaux modèles GS 3D est menée et évaluée sur diverses tâches de référence afin de mettre en évidence leurs performances et leur praticité. L'analyse se termine en identifiant les défis actuels et en suggérant des pistes potentielles pour de futures recherches dans ce domaine. Avec cette enquête, nous visons à fournir aux chercheurs débutants et expérimentés une ressource précieuse, stimulant une exploration plus approfondie et des progrès dans les représentations applicables et sans ambiguïté des champs de rayonnement.

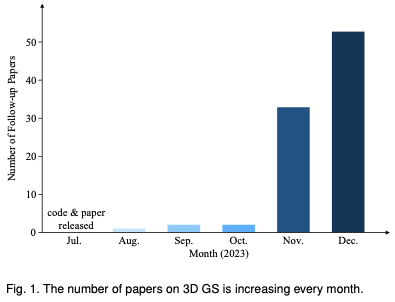
Pour aider les lecteurs à suivre le développement rapide de 3D GS, nous proposons la première enquête sur 3D GS. Nous avons systématiquement et en temps opportun rassemblé la littérature la plus récente et la plus importante sur ce sujet, principalement provenant d'arxiv. L'objectif de cet article est de fournir une analyse complète et à jour du développement initial, des fondements théoriques et des applications émergentes de 3D GS, soulignant son potentiel révolutionnaire dans le domaine. Compte tenu de la nature naissante mais en évolution rapide de la 3D GS, cette enquête vise également à identifier et discuter des défis actuels et des perspectives d'avenir dans ce domaine. Nous fournissons un aperçu des orientations de recherche en cours et des avancées potentielles que 3D GS peut faciliter. Nous espérons que cette étude fournira non seulement des connaissances académiques, mais stimulera également la poursuite de la recherche et de l'innovation dans ce domaine. La structure de cet article est la suivante : (Figure 2) Veuillez noter que tout le contenu est basé sur la littérature et les résultats de recherche les plus récents et vise à fournir aux lecteurs des informations complètes et actuelles sur 3D GS.

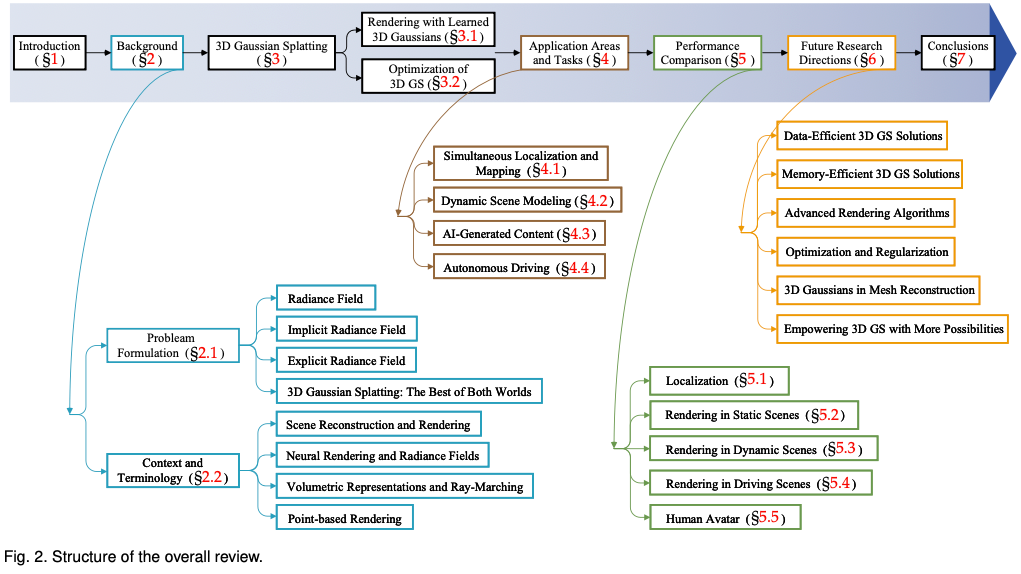
Introduction au contexte

Cette section présente la brève formule du champ de rayonnement, qui est un concept clé dans le rendu de scène. Les champs de rayonnement peuvent être représentés par deux types principaux : implicites, comme NeRF, qui utilise des réseaux de neurones pour un rendu direct mais exigeant en termes de calcul ; et explicites, comme les maillages, qui utilisent des structures discrètes pour un accès plus rapide mais une utilisation moindre de la mémoire. Ensuite, nous explorerons plus en détail les liens avec des domaines connexes tels que la reconstruction et le rendu de scènes.

Définition du problème

Champ de rayonnement : Un champ de rayonnement est une représentation de la distribution de la lumière dans un espace tridimensionnel, qui capture la manière dont la lumière interagit avec les surfaces et les matériaux de l'environnement. Mathématiquement, un champ de rayonnement peut être décrit comme une fonction qui mappe un point dans l'espace et une direction spécifiée par des coordonnées sphériques à des valeurs de rayonnement non négatives. Les champs de rayonnement peuvent être encapsulés par des représentations implicites ou explicites, chacune présentant des avantages spécifiques en matière de représentation de scène et de rendu.

Champ de rayonnement implicite : Un champ de rayonnement implicite représente la distribution de la lumière dans une scène sans définir explicitement la géométrie de la scène. À l’ère de l’apprentissage profond, il utilise souvent des réseaux de neurones pour apprendre des représentations volumétriques continues de scènes. L’exemple le plus frappant est NeRF. Dans NeRF, un réseau MLP est utilisé pour mapper un ensemble de coordonnées spatiales et de directions de visualisation aux valeurs de couleur et de densité. La radiance d'un point quelconque n'est pas stockée explicitement mais est calculée en temps réel en interrogeant le réseau neuronal. Par conséquent, la fonction peut s'écrire comme suit :

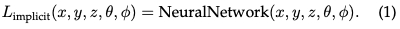
Ce format permet une représentation compacte et différentiable de scènes complexes, bien qu'avec une charge de calcul plus élevée lors du rendu en raison du déplacement volumétrique des rayons.

Champs de rayonnement explicites : En revanche, les champs de rayonnement explicites représentent directement la distribution de la lumière dans une structure spatiale discrète, telle qu'une grille de voxels ou un ensemble de points. Chaque élément de la structure stocke des informations de rayonnement pour sa position correspondante dans l'espace. Cette approche permet un accès plus direct et souvent plus rapide aux données radiométriques, mais au prix d'une utilisation plus importante de la mémoire et d'une résolution potentiellement inférieure. La forme générale de la représentation explicite du champ de rayonnement peut s'écrire :

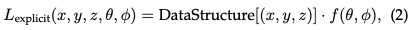
Où DataStructure peut être une grille ou un nuage de points, qui est une fonction qui modifie le rayonnement en fonction de la direction de visualisation.

Le meilleur des deux mondes 3D Gaussian Splatting : 3D GS représente la transition des champs de rayonnement implicites aux champs de rayonnement explicites. Il exploite les avantages des deux méthodes en exploitant les gaussiennes 3D comme représentation flexible et efficace. Ces coefficients gaussiens sont optimisés pour représenter avec précision la scène, combinant les avantages de l'optimisation basée sur les réseaux neuronaux et du stockage de données structurées explicites. Cette approche hybride vise à obtenir un rendu de haute qualité avec un entraînement plus rapide et des performances en temps réel, en particulier pour les scènes complexes et les sorties haute résolution. La représentation gaussienne 3D est formulée comme suit :

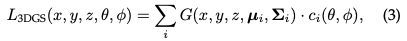
Contexte et terminologie

De nombreuses technologies et disciplines de recherche sont étroitement liées à la GS 3D, qui seront brièvement décrites ci-dessous.

Reconstruction et rendu de scène : En gros, la reconstruction de scène implique la création d'un modèle 3D d'une scène à partir d'une collection d'images ou d'autres données. Le rendu est un terme plus spécifique qui se concentre sur la conversion d'informations lisibles par ordinateur (par exemple, des objets 3D dans une scène) en images pixelisées. Les premières techniques étaient basées sur des champs lumineux pour générer des images réalistes. Les algorithmes de structure à partir du mouvement (SfM) et de stéréo multi-vues (MVS) font progresser le domaine en estimant la structure 3D à partir de séquences d'images. Ces méthodes historiques ont jeté les bases de techniques de reconstruction et de rendu de scènes plus complexes.

Rendu neuronal avec champs radiants : le rendu neuronal combine l'apprentissage en profondeur avec des techniques graphiques traditionnelles pour créer des images photoréalistes. Les premières tentatives utilisaient des réseaux de neurones convolutifs (CNN) pour estimer des poids hybrides ou des solutions d'espace de texture. Un champ de rayonnement représente une fonction qui décrit la quantité de lumière se propageant dans chaque direction à travers chaque point de l'espace. Les NeRF utilisent des réseaux de neurones pour modéliser les champs de rayonnement, permettant un rendu de scène détaillé et réaliste.

Représentation volumique et Ray-Marching : La représentation volumique modélise les objets et les scènes non seulement comme des surfaces, mais aussi comme des volumes remplis de matériaux ou d'espace vide. Cette méthode permet un rendu plus précis de phénomènes tels que le brouillard, la fumée ou les matériaux translucides. Ray-Marching est une technique utilisée avec des représentations volumétriques pour restituer des images en traçant progressivement le chemin de la lumière à travers un volume. NeRF partage le même esprit de marche de rayons volumétriques et introduit l'importance de l'échantillonnage et du codage de position pour améliorer la qualité des images synthétisées. Tout en fournissant des résultats de haute qualité, le déplacement des rayons de volume est coûteux en calcul, ce qui incite à rechercher des méthodes plus efficaces telles que la 3D GS.

Rendu basé sur des points : Le rendu basé sur des points est une technique permettant de visualiser des scènes 3D en utilisant des points au lieu de polygones traditionnels. Cette approche est particulièrement efficace pour restituer des données géométriques complexes, non structurées ou clairsemées. Les points peuvent être améliorés avec des propriétés supplémentaires, telles que des descripteurs neuronaux apprenables, et rendus efficacement, mais cette approche peut souffrir de problèmes tels que des trous ou des effets d'alias dans le rendu. 3D GS étend ce concept en utilisant des gaussiennes anisotropes pour obtenir une représentation plus continue et cohérente de la scène.

3D Gaussian for Explicit Radiation Fields

3D GS est une avancée majeure dans le rendu d'images haute résolution en temps réel sans recourir à des composants neuronaux.

Gaussiens 3D appris pour une nouvelle synthèse de perspective

Considérez une scène représentée par (des millions de) Gaussiens 3D optimisés. L'objectif est de générer une image basée sur une pose de caméra spécifiée. Rappelons que NeRF accomplit cette tâche en exigeant un déplacement de rayon volumétrique, en échantillonnant un point spatial 3D pour chaque pixel. Ce mode rend difficile la synthèse d'images haute résolution et ne permet pas d'atteindre une vitesse de rendu en temps réel. À l'opposé, 3D GS projette d'abord ces gaussiennes 3D sur un plan d'image basé sur des pixels, un processus appelé « éclaboussement » (Fig. 3a). 3D GS trie ensuite ces gaussiennes et calcule la valeur de chaque pixel. Comme le montre la figure, le rendu de NeRF et de 3D GS peut être considéré comme le processus inverse l'un de l'autre. Dans ce qui suit, nous commençons par la définition d'une gaussienne 3D, qui est le plus petit élément de représentation de scène dans un GS 3D. Nous décrivons ensuite comment utiliser ces Gaussiennes 3D pour un rendu différentiable. Enfin, la technologie d'accélération utilisée dans 3D GS est introduite, qui est la clé d'un rendu rapide.

Propriétés de la gaussienne tridimensionnelle : Les caractéristiques de la gaussienne tridimensionnelle sont son centre (position) μ, son opacité α, sa matrice de covariance tridimensionnelle ∑ et sa couleur c. Pour l'apparence dépendant de la vue, c est représenté par les harmoniques sphériques. Tous les attributs peuvent être appris et optimisés via la rétropropagation.

Frustum Culling : Étant donné une pose de caméra spécifiée, cette étape détermine quelles gaussiennes 3D se trouvent à l'extérieur du tronc de la caméra. En faisant cela, les Gaussiennes 3D en dehors d'une vue donnée ne seront pas impliquées dans les calculs ultérieurs, économisant ainsi les ressources de calcul.

Splatting : ** Dans cette étape, une gaussienne 3D (ellipsoïde) est projetée dans un espace image 2D (ellipsoïde) pour le rendu. Étant donné une transformation de visualisation W et une matrice de covariance 3D Σ, la matrice de covariance 2D projetée Σ′ est calculée à l'aide de la formule suivante :

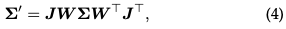
où J est la matrice jacobienne de l'approximation affine de la transformation projective.

Rendu des pixels : Avant de plonger dans la version finale de 3D GS, nous détaillons d'abord sa forme la plus simple pour mieux comprendre son fonctionnement. 3D GS utilise plusieurs technologies pour faciliter le calcul parallèle. Étant donné la position d'un pixel La synthèse alpha est ensuite utilisée pour calculer la couleur finale de ce pixel :

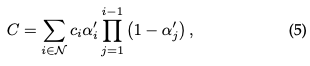
où est la couleur apprise et l'opacité finale est le produit de l'opacité apprise et de la valeur gaussienne :

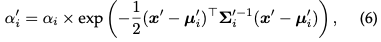
où x′ et μ sont les coordonnées dans l’espace de projection. Étant donné qu'il est difficile de paralléliser la génération des listes triées requises, le processus de rendu décrit peut être plus lent que celui du NeRF, ce qui constitue une préoccupation légitime. En fait, cette préoccupation est valable ; la vitesse de rendu peut être considérablement affectée lors de l’utilisation de cette approche simple pixel par pixel. Afin d'obtenir un rendu en temps réel, 3DGS a fait quelques concessions pour s'adapter au calcul parallèle.

Tuiles (patchs) : Pour éviter le coût de calcul lié à la dérivation de coefficients gaussiens pour chaque pixel, 3D GS transfère la précision du niveau de pixel au niveau de détail du patch. Plus précisément, 3D GS divise initialement l'image en plusieurs blocs qui ne se chevauchent pas, appelés « tuiles » dans le document original. La figure 3b fournit une illustration de tuiles. Chaque tuile se compose de 16×16 pixels. 3D GS détermine en outre quelles tuiles croisent ces cartes gaussiennes projetées. En supposant que la gaussienne projetée puisse couvrir plusieurs tuiles, l'approche logique consiste à copier la gaussienne, en attribuant à chaque copie l'identifiant de la tuile concernée (c'est-à-dire l'ID de la tuile).

Rendu parallèle : Après la copie, 3D GS combine les ID de tuile individuels avec les valeurs de profondeur obtenues à partir de la transformation de vue de chaque gaussienne. Cela produit une liste d'octets non triée, où les bits de poids fort représentent l'ID de tuile et les bits de poids faible représentent la profondeur. En faisant cela, la liste triée peut être utilisée directement pour le rendu (c'est-à-dire la composition alpha). Les figures 3c et 3d fournissent des démonstrations visuelles de ces concepts. Il convient de souligner que le rendu de chaque tuile et pixel s’effectue indépendamment, ce qui rend ce processus idéal pour le calcul parallèle. Un autre avantage est que les pixels de chaque tuile ont accès à une mémoire partagée commune et maintiennent une séquence de lecture uniforme, permettant ainsi d'effectuer la composition alpha en parallèle avec une plus grande efficacité. Dans la mise en œuvre officielle de l'article original, le framework traite respectivement le traitement des tuiles et des pixels comme similaire aux blocs et aux threads de l'architecture de programmation CUDA.

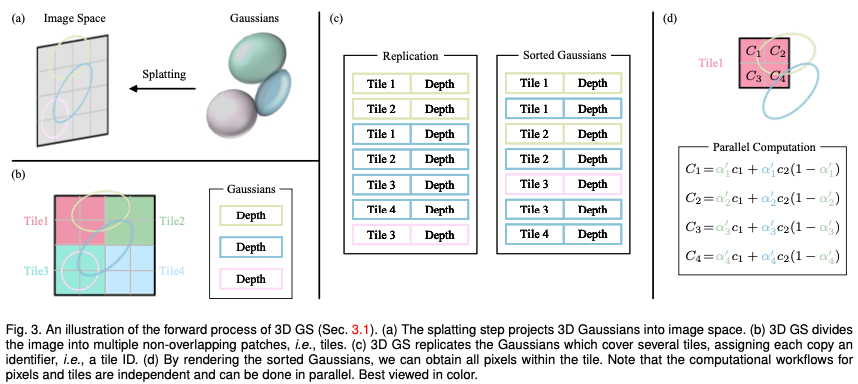
En bref, 3D GS introduit plusieurs approximations dans l'étape de traitement direct pour améliorer l'efficacité des calculs tout en maintenant un niveau élevé de qualité de synthèse d'image.

Optimisation des éclaboussures gaussiennes 3D

Au cœur de 3D GS se trouve un processus d'optimisation conçu pour créer une large collection de gaussiennes 3D qui capturent avec précision l'essence de la scène, facilitant ainsi le rendu avec un point de vue libre. D'une part, les propriétés des Gaussiennes 3D doivent être optimisées via un rendu différenciable pour s'adapter à la texture d'une scène donnée. En revanche, le nombre de Gaussiennes 3D pouvant bien représenter une scène donnée n’est pas connu à l’avance. Une approche prometteuse consiste à faire en sorte que les réseaux de neurones apprennent automatiquement les densités gaussiennes 3D. Nous verrons comment optimiser les propriétés de chaque gaussienne et comment contrôler la densité des gaussiennes. Ces deux processus sont entrelacés dans le flux de travail d'optimisation. Étant donné qu'il existe de nombreux hyperparamètres définis manuellement lors de l'optimisation, nous omettons les symboles de la plupart des hyperparamètres par souci de clarté.

Optimisation des paramètres

Fonction de perte : Une fois la synthèse de l'image terminée, la perte est calculée comme la différence entre l'image rendue et le GT :

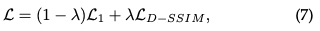
La fonction de perte de 3D-GS est légèrement différent de celui des NeRF. En raison du temps de marche des rayons, NeRF est généralement calculé au niveau des pixels plutôt qu'au niveau de l'image.

Mise à jour des paramètres : La plupart des propriétés de la gaussienne 3D peuvent être optimisées directement par rétropropagation. Il est à noter que l'optimisation directe de la matrice de covariance Σ conduit à une matrice semi-définie non positive, qui n'est pas conforme à l'interprétation physique habituellement associée à la matrice de covariance. Pour éviter ce problème, 3D GS choisit d'optimiser le quaternion q et le vecteur 3D s. q et s représentent respectivement la rotation et la mise à l'échelle. Cette approche permet de reconstruire la matrice de covariance ∑ comme suit :

Contrôle de la densité

Initialisation : 3D GS démarre à partir d'un ensemble initial de SfM ou de points clairsemés initialisés de manière aléatoire. Ensuite, la densification ponctuelle et l’élagage sont utilisés pour contrôler la densité des gaussiennes tridimensionnelles.

Densification des points : Dans l'étape de densification des points, 3D GS augmente de manière adaptative la densité gaussienne pour mieux capturer les détails de la scène. Ce processus accorde une attention particulière aux zones où les caractéristiques géométriques sont absentes ou où la distribution gaussienne est trop dispersée. La densification est effectuée après un certain nombre d'itérations, ciblant les gaussiennes qui présentent de grands gradients de position dans l'espace de visualisation (c'est-à-dire au-dessus d'un certain seuil). Cela implique de cloner une petite gaussienne dans des zones sous-reconstruites ou de diviser une grande gaussienne dans des zones sur-reconstruites. Pour le clonage, une copie de la gaussienne est créée et déplacée vers le dégradé de position. Pour le fractionnement, deux gaussiennes plus petites remplacent une gaussienne plus grande, réduisant ainsi leur taille d'un facteur spécifique. Cette étape recherche la distribution et la représentation optimales des gaussiennes dans l'espace 3D, améliorant ainsi la qualité globale de la reconstruction.

Élagage ponctuel : L'étape d'élagage ponctuel consiste à supprimer les gaussiennes redondantes ou moins influentes, ce qui peut être considéré dans une certaine mesure comme un processus de régularisation. Cette étape est réalisée en éliminant les gaussiennes presque transparentes (α en dessous d'un seuil spécifié) et les gaussiennes trop grandes dans l'espace mondial ou dans l'espace de visualisation. De plus, pour éviter une augmentation déraisonnable de la densité des gaussiennes à proximité de la caméra d'entrée, la valeur alpha des gaussiennes est fixée proche de zéro après un certain nombre d'itérations. Cela permet de contrôler l’augmentation nécessaire de la densité des Gaussiennes tout en éliminant les Gaussiennes en excès. Ce processus permet non seulement d'économiser des ressources informatiques, mais garantit également que la représentation de la scène par les gaussiennes dans le modèle reste précise et efficace.

Domaines d'application et tâches

Le potentiel de transformation de 3D GS s'étend bien au-delà de ses avancées théoriques et informatiques. Cette section explore divers domaines d'application pionniers dans lesquels la 3D GS a un impact significatif, tels que la robotique, la reconstruction et la représentation de scènes, le contenu généré par l'IA, la conduite autonome et même d'autres disciplines scientifiques. L'application du 3D GS démontre sa polyvalence et son potentiel révolutionnaire. Nous décrivons ici certains des domaines d'application les plus remarquables, en donnant un aperçu de la manière dont la 3D GS trace de nouvelles frontières dans chaque domaine.

SLAM

SLAM est un problème informatique central pour la robotique et les systèmes autonomes. Il s’agit du défi d’un robot ou d’un appareil comprenant sa position dans un environnement inconnu tout en cartographiant la configuration de l’environnement. Le SLAM est essentiel dans diverses applications, notamment les voitures autonomes, la réalité augmentée et la navigation des robots. Le cœur de SLAM est de créer une carte de l’environnement inconnu et de déterminer l’emplacement de l’appareil sur la carte en temps réel. Par conséquent, SLAM pose un énorme défi à la technologie de représentation de scènes à forte intensité de calcul et constitue également un bon banc d'essai pour 3D GS.

3D GS entre dans le domaine du SLAM en tant que méthode innovante de représentation de scène. Les systèmes SLAM traditionnels utilisent généralement des nuages ​​de points/surfaces ou des maillages voxels pour représenter l'environnement. En revanche, 3D GS utilise des gaussiennes anisotropes pour mieux représenter l'environnement. Cette représentation offre plusieurs avantages : 1) Efficacité : contrôlez de manière adaptative la densité des gaussiennes 3D pour représenter de manière compacte les données spatiales et réduire la charge de calcul. 2) Précision : la gaussienne anisotrope permet une modélisation de l'environnement plus détaillée et plus précise, particulièrement adaptée aux scènes complexes ou changeantes dynamiquement. 3) Adaptabilité : 3D GS peut s'adapter à différentes échelles et environnements complexes, ce qui le rend adapté à différentes applications SLAM. Plusieurs études innovantes ont utilisé l'éclaboussement gaussien 3D dans SLAM, démontrant le potentiel et la polyvalence de ce paradigme.

Modélisation dynamique de scène

La modélisation dynamique de scène fait référence au processus de capture et de représentation de la structure tridimensionnelle et de l'apparence d'une scène qui change au fil du temps. Cela implique de créer un modèle numérique qui reflète avec précision la géométrie, le mouvement et les aspects visuels des objets de la scène. La modélisation dynamique de scènes est essentielle dans diverses applications, notamment la réalité virtuelle et augmentée, l'animation 3D et la vision par ordinateur. La diffusion gaussienne 4D (4D GS) étend le concept de 3D GS aux scènes dynamiques. Il intègre la dimension temporelle, permettant la représentation et le rendu de scènes qui évoluent au fil du temps. Ce paradigme apporte des améliorations significatives dans le rendu des scènes dynamiques en temps réel tout en conservant une sortie visuelle de haute qualité.

AIGC

AIGC fait référence à un contenu numérique créé de manière autonome ou modifié de manière significative par des systèmes d'intelligence artificielle, notamment dans les domaines de la vision par ordinateur, du traitement du langage naturel et de l'apprentissage automatique. AIGC se caractérise par sa capacité à simuler, étendre ou améliorer le contenu généré artificiellement, permettant des applications allant de la synthèse d'images photoréalistes à la création narrative dynamique. L’importance de l’AIGC réside dans son potentiel de transformation dans divers domaines, notamment le divertissement, l’éducation et le développement technologique. Il s’agit d’un élément clé dans le paysage évolutif de la création de contenu numérique, offrant une alternative évolutive, personnalisable et souvent plus efficace aux méthodes traditionnelles.

Cette fonctionnalité sans ambiguïté de 3D GS facilite les capacités de rendu en temps réel et un niveau de contrôle et d'édition sans précédent, ce qui la rend très pertinente pour les applications AIGC. La représentation explicite de la scène et l'algorithme de rendu différenciable de 3D GS répondent pleinement aux exigences de l'AIGC en matière de génération de contenu haute fidélité, en temps réel et modifiable, ce qui est crucial pour les applications de réalité virtuelle, de médias interactifs et d'autres domaines.

Conduite autonome

La conduite autonome est conçue pour permettre aux véhicules de naviguer et de fonctionner sans intervention humaine. Ces véhicules sont équipés d'une suite de capteurs, notamment de caméras, de LiDAR et de radar, combinés à des algorithmes avancés, des modèles d'apprentissage automatique et une puissante puissance de calcul. L’objectif principal est de détecter l’environnement, de prendre des décisions éclairées et d’exécuter des manœuvres de manière sûre et efficace. La conduite autonome a le potentiel de transformer les transports, offrant des avantages clés tels que l'amélioration de la sécurité routière en réduisant les erreurs humaines, l'amélioration de la mobilité pour ceux qui ne peuvent pas conduire et l'optimisation de la circulation, réduisant ainsi les embouteillages et l'impact environnemental.

Les voitures autonomes doivent détecter et interpréter l'environnement qui les entoure afin de conduire en toute sécurité. Cela inclut la reconstruction des scènes de conduite en temps réel, l'identification précise des objets statiques et dynamiques et la compréhension de leurs relations spatiales et de leurs mouvements. Dans les scénarios de conduite dynamique, l'environnement change constamment en raison des objets en mouvement tels que d'autres véhicules, des piétons ou des animaux. Reconstruire avec précision ces scènes en temps réel est essentiel pour une navigation sûre, mais constitue un défi en raison de la complexité et de la variabilité des éléments impliqués. En conduite autonome, la 3D GS peut être utilisée pour reconstruire des scènes en mélangeant des points de données, tels que ceux obtenus à partir de capteurs tels que LiDAR, dans une représentation cohérente et continue. Ceci est particulièrement utile pour gérer différentes densités de points de données et garantir une reconstruction fluide et précise des arrière-plans statiques et des objets dynamiques dans une scène. Jusqu'à présent, peu de travaux utilisent la gaussienne 3D pour modéliser des scènes dynamiques de conduite/de rue et montrent d'excellentes performances en matière de reconstruction de scène par rapport aux méthodes existantes.

Comparaison des performances

Cette section fournit plus de preuves empiriques en montrant les performances de plusieurs algorithmes GS 3D dont nous avons discuté précédemment. Les diverses applications de 3D GS dans de nombreuses tâches, associées à la conception d’algorithmes personnalisés pour chaque tâche, rendent peu pratique une comparaison uniforme de tous les algorithmes 3D GS au sein d’une seule tâche ou d’un seul ensemble de données. Par conséquent, nous sélectionnons trois tâches représentatives dans le domaine 3D GS pour une évaluation approfondie des performances. Les performances proviennent principalement des documents originaux, sauf indication contraire. Performances de rendu de scène statique

Performance Humaine Digitale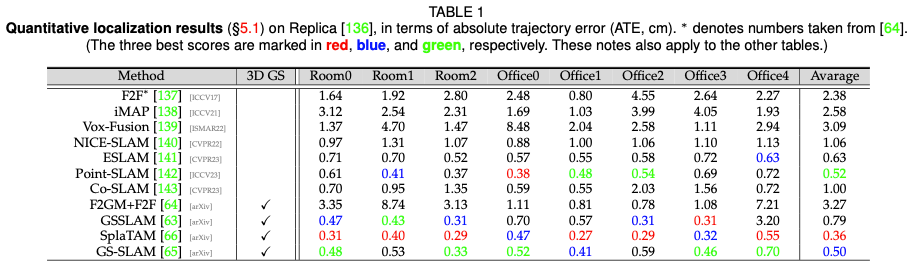

Orientations futures de la recherche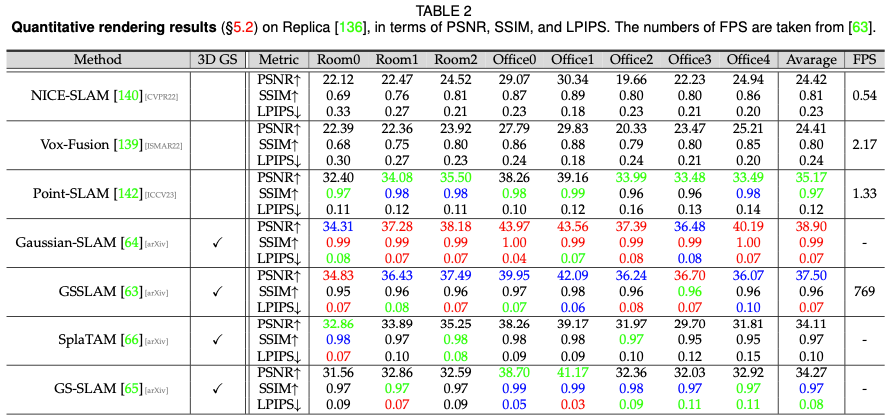

Bien que les travaux de suivi sur 3D GS aient fait des progrès significatifs ces derniers mois, nous pensons qu'il reste encore certains défis à surmonter.

• Solutions 3D GS économes en données : générer de nouvelles vues et reconstruire des scènes à partir de points de données limités présente un grand intérêt, d'autant plus qu'elles ont le potentiel d'améliorer le réalisme et l'expérience utilisateur avec une contribution minimale. Des progrès récents ont exploré l'utilisation d'informations sur la profondeur, de distributions de probabilité denses et de cartographie pixel-gaussienne pour faciliter cette capacité. Cependant, des explorations plus approfondies dans ce domaine restent nécessaires de toute urgence. De plus, un problème important de la GS 3D est l’apparition d’artefacts dans des zones où les données d’observation sont insuffisantes. Ce défi constitue une limitation courante dans le rendu des champs de rayonnement, car des données éparses conduisent souvent à des reconstructions inexactes. Par conséquent, le développement de nouvelles méthodes d’interpolation ou d’intégration de données dans ces régions clairsemées représente une voie prometteuse pour les recherches futures.
• Solution 3D GS économe en mémoire : bien que 3D GS démontre des capacités extraordinaires, son évolutivité pose des défis importants, en particulier lorsqu'il est associé à des approches basées sur NeRF. Ce dernier bénéficie de la simplicité de stocker uniquement les paramètres du MLP appris. Ce problème d'évolutivité devient de plus en plus grave dans le contexte de la gestion de scènes à grande échelle, où les besoins en calcul et en mémoire augmentent considérablement. Par conséquent, il existe un besoin urgent d’optimiser l’utilisation de la mémoire pendant la phase de formation et de stockage du modèle. L'exploration de structures de données plus efficaces et l'étude de techniques de compression avancées sont des voies prometteuses pour remédier à ces limitations.
• Algorithme de rendu avancé : le pipeline de rendu actuel de 3D GS est tourné vers l'avenir et peut être encore optimisé. Par exemple, un simple algorithme de visibilité peut provoquer un changement radical de l’ordre de profondeur/mélange gaussien. Cela met en évidence une opportunité importante pour les recherches futures : la mise en œuvre d’algorithmes de rendu plus avancés. Ces méthodes améliorées devraient viser à simuler plus précisément les interactions complexes entre la lumière et les propriétés des matériaux dans une scène donnée. Une approche prometteuse pourrait impliquer l’assimilation et l’adaptation des principes établis de l’infographie traditionnelle au contexte spécifique de la 3D GS. Il convient de noter à cet égard les efforts en cours pour intégrer des techniques de rendu améliorées ou des modèles hybrides dans le cadre informatique actuel de 3D GS. De plus, l’exploration du rendu inverse et de ses applications constitue un terrain fertile pour la recherche.
• Optimisation et régularisation : bien que les gaussiennes anisotropes soient utiles pour représenter des géométries complexes, elles peuvent produire des artefacts visuels. Par exemple, ces grandes Gaussiennes 3D, en particulier dans les zones dont l'apparence dépend de la vue, peuvent provoquer des artefacts pop-in, où des éléments visuels apparaissent ou disparaissent soudainement, interrompant l'immersion. Il existe un potentiel d’exploration considérable dans la régularisation et l’optimisation de 3D GS. L'introduction de l'anticrénelage peut atténuer les changements soudains de profondeur gaussienne et d'ordre de fusion. Les améliorations apportées à l'algorithme d'optimisation peuvent permettre un meilleur contrôle des coefficients gaussiens dans l'espace. De plus, l’intégration de la régularisation dans le processus d’optimisation peut accélérer la convergence, atténuer le bruit visuel ou améliorer la qualité de l’image. De plus, un si grand nombre d’hyperparamètres affecte la généralisation de la 3D GS, qui nécessite de toute urgence des solutions.
• Gaussiennes 3D dans la reconstruction de maillage : le potentiel de la GS 3D dans la reconstruction de maillage et sa place dans le spectre des représentations de volumes et de surfaces doivent encore être pleinement explorés. Il existe un besoin urgent d’étudier comment les primitives gaussiennes conviennent aux tâches de reconstruction de maillage. Cette exploration pourrait combler le fossé entre le rendu volumétrique et les méthodes traditionnelles basées sur les surfaces, en fournissant un aperçu de nouvelles techniques et applications de rendu.
• Donner à la 3D GS plus de possibilités : malgré l'énorme potentiel de la 3D GS, la gamme complète des applications de la 3D GS reste largement inexplorée. Une voie prometteuse à explorer consiste à améliorer les Gaussiennes 3D avec des propriétés supplémentaires, telles que des propriétés linguistiques et physiques adaptées à des applications spécifiques. En outre, des recherches récentes ont commencé à révéler les capacités de la 3D GS dans plusieurs domaines, tels que l'estimation de la pose de la caméra, la capture des interactions main-objet et la quantification de l'incertitude. Ces résultats préliminaires offrent aux chercheurs interdisciplinaires d’importantes opportunités d’explorer davantage la GS 3D.

Conclusion

À notre connaissance, cette revue fournit le premier aperçu complet de 3D GS, un champ de rayonnement explicite révolutionnaire et une technologie d'infographie. Il représente un changement de paradigme par rapport aux méthodes NeRF traditionnelles, mettant en évidence les avantages de la 3D GS en termes de rendu en temps réel et de contrôlabilité améliorée. Notre analyse détaillée démontre les avantages de 3D GS dans les applications du monde réel, en particulier celles nécessitant des performances en temps réel. Nous fournissons un aperçu des orientations futures de la recherche et des défis non résolus dans le domaine. Dans l’ensemble, 3D GS est une technologie transformatrice qui devrait avoir un impact significatif sur le développement futur de la reconstruction et de la représentation 3D. Cette enquête est destinée à servir de ressource fondamentale pour stimuler l’exploration et les progrès dans ce domaine en développement rapide.

Lien original : https://mp.weixin.qq.com/s/jH4g4Cx87nPUYN8iKaKcBA

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!