Maison >tutoriels informatiques >connaissances en informatique >Comment utiliser l'angle de phase φ dans la fonction trigonométrique y=Asin(wx+φ)
Comment utiliser l'angle de phase φ dans la fonction trigonométrique y=Asin(wx+φ)
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2024-01-15 22:06:111120parcourir
Qu'en est-il de φ dans la fonction trigonométrique y Asinwx φ
1. Méthode des points clés :
Lors de la détermination de la valeur φ, considérez l'intersection de la fonction y=Asin(ωx+φ)+B et l'axe des x. Nous devons trouver l’abscisse du point qui coupe initialement l’axe des x, c’est-à-dire soit ωx+φ=0. De cette façon, la valeur de φ peut être déterminée. Afin de choisir le bon point à substituer dans la formule analytique, nous devons faire attention à quel point de la « méthode en cinq points » le point appartient. Dans la « méthode des cinq points », on choisit le « premier point », qui fait référence au point où l'image coupe l'axe des x lorsqu'elle monte. Par conséquent, ωx+φ=0 à ce moment. Veuillez noter que votre réponse ne peut excéder 112 mots.
Quand le "point maximum" (c'est-à-dire le "point culminant" de l'image)
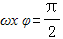
Quand le "point minimum" (c'est-à-dire le "point de vallée" de l'image)
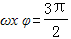
2. Méthode de substitution :
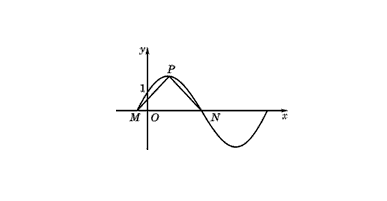
Les valeurs de A, ω et B peuvent être déterminées en substituant des points connus dans l'équation ou en résolvant l'intersection de l'image et de la ligne droite. Faites attention à l'emplacement de l'intersection.
Informations détaillées :
Méthode de monotonie de la fonction trigonométrique y=Asin(ωx+φ):
1. Nous pouvons comprendre la monotonie de la fonction y=Asin(ωx+φ) du point de vue des fonctions composites. La monotonie d'une fonction composite est déterminée à la fois par la fonction interne et la fonction externe.
Si la monotonie de la fonction interne et de la fonction externe est la même dans un certain intervalle, la fonction composite est une fonction croissante. Si la monotonie de la fonction interne et de la fonction externe est opposée dans un certain intervalle, la fonction composite est une fonction décroissante. Bref, à la fois augmenter et diminuer.
2. L'image de la fonction y=Asin (ωx+φ) est obtenue par la fonction y=sinx par étirement et transformation de translation. La monotonie de la fonction y=Asin(ωx+φ) est également résolue à partir de la fonction y=sinx.
La fonction y=Asin (ωx+φ) peut être considérée comme un composite de la fonction y=sint et de la fonction t=ωx+φ. La fonction t=ωx+φ est une fonction linéaire et sa monotonie est déterminée par le signe de ω.
Il suffit donc de considérer (ωx+φ) dans son ensemble et de le substituer dans l'intervalle monotone de y=sint.
Par exemple, l'intervalle croissant monotone de la fonction y=sint est [-(π/2)+2kπ, (π/2)+2kπ], alors on peut remplacer t dans son ensemble par ωx+φ, c'est-à-dire -( π/2)+ 2kπ≤ωx+φ≤(π/2)+2kπ.
Il suffit de résoudre l'inégalité - (π/2) + 2kπ ≤ (ωx + φ) ≤ (π/2) + 2kπ pour obtenir l'intervalle monotone de la fonction y = Asin (ωx + φ).
3. Afin de réduire la difficulté de l'analyse, nous utilisons généralement la formule de récurrence pour changer ω dans la fonction y=Asin (ωx+φ) en un nombre positif, afin de pouvoir garantir que la fonction linéaire t=ωx+ φ sur l'ensemble de nombres réels est une fonction croissante.
Nous savons d'après les propriétés des fonctions composites que si nous voulons l'intervalle d'augmentation (diminution) monotone de la fonction y=Asin (ωx+φ), nous amènerons le tout (ωx+φ) dans l'intervalle d'augmentation (diminution) monotone de la fonction y=sint, puis combinez le positif et le négatif de A, et enfin résolvez la plage de x. La plage x résolue est l'intervalle monotone de la fonction y=Asin(ωx+φ).
Source de référence : Encyclopédie - Fonctions trigonométriques
Formule de pente d'une ligne droite
La formule de calcul de la pente d'une droite : k=(y2-y1)/(x2-x1)
La tangente de l'angle formé par une droite et l'axe X à droite.
k=tanα=(y2-y1)/(x2-x1) ou (y1-y2)/(x1-x2)
Lorsque la pente de la droite L existe, pour la fonction linéaire y=kx+b (forme d'intersection de pente), k est la pente de la fonction image (droite).
Informations détaillées
Lorsque la pente de la droite L n'existe pas, la formule d'origine de la pente y=kx+b Quand k=0 y=b
Lorsque la pente de la droite L existe, la formule de pente du point y2—y1=k(X2—X1),
Lorsque la droite L a une origine non nulle sur les deux axes de coordonnées, il existe une formule d'origine X/a+y/b=1
Pour tout point de n'importe quelle fonction, sa pente est égale à l'angle entre sa tangente et la direction positive de l'axe des x, c'est-à-dire tanα
Calcul de la pente : ax+by+c=0, k=-a/b.
Formule de pente de ligne : k=(y2-y1)/(x2-x1)
Le produit des pentes de deux droites perpendiculaires sécantes est -1:k1*k2=-1.
Quand k>0, plus l'angle entre la droite et l'axe des x est grand, plus la pente est grande ; lorsque k
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

