Récemment, un article a été publié sur arxiv, qui fournit une nouvelle interprétation des principes mathématiques de Transformer. Le contenu est très long et il y a beaucoup de connaissances. Je recommande fortement de lire l'article original.
En 2017, « L'attention est tout ce dont vous avez besoin » publié par Vaswani et al. est devenu une étape importante dans le développement de l'architecture des réseaux neuronaux. La principale contribution de cet article est le mécanisme d'auto-attention, qui est l'innovation qui distingue les Transformers des architectures traditionnelles et joue un rôle important dans ses excellentes performances pratiques. En fait, cette innovation est devenue un catalyseur clé pour l'avancement de l'intelligence artificielle dans des domaines tels que la vision par ordinateur et le traitement du langage naturel, tout en jouant également un rôle clé dans l'émergence de grands modèles de langage. Par conséquent, comprendre les transformateurs, et en particulier les mécanismes par lesquels l’attention personnelle traite les données, est un domaine crucial mais largement sous-étudié. 
Adresse papier : https://arxiv.org/pdf/2312.10794.pdfLes réseaux de neurones profonds (DNN) ont une caractéristique commune : les données d'entrée sont traitées couche par couche dans l'ordre, formant un Système dynamique discret temporel (pour un contenu spécifique, veuillez vous référer au « Deep Learning » publié par le MIT, également connu sous le nom de « Flower Book » en Chine). Cette perspective a été utilisée avec succès pour modéliser des réseaux résiduels sur des systèmes dynamiques continus dans le temps, appelés équations différentielles ordinaires neuronales (ODE neuronales). Dans l'équation différentielle constante divine, l'image d'entrée  évoluera en fonction du champ de vitesse variable dans le temps donné
évoluera en fonction du champ de vitesse variable dans le temps donné  sur l'intervalle de temps (0, T). Par conséquent, le DNN peut être considéré comme une Flow Map
sur l'intervalle de temps (0, T). Par conséquent, le DNN peut être considéré comme une Flow Map  d’un
d’un  à un autre
à un autre  . Il existe une forte similitude entre les cartes de flux même dans les champs de vitesse
. Il existe une forte similitude entre les cartes de flux même dans les champs de vitesse  sous les contraintes des architectures DNN classiques. Les chercheurs ont découvert que les transformateurs sont en fait des mappages de flux sur
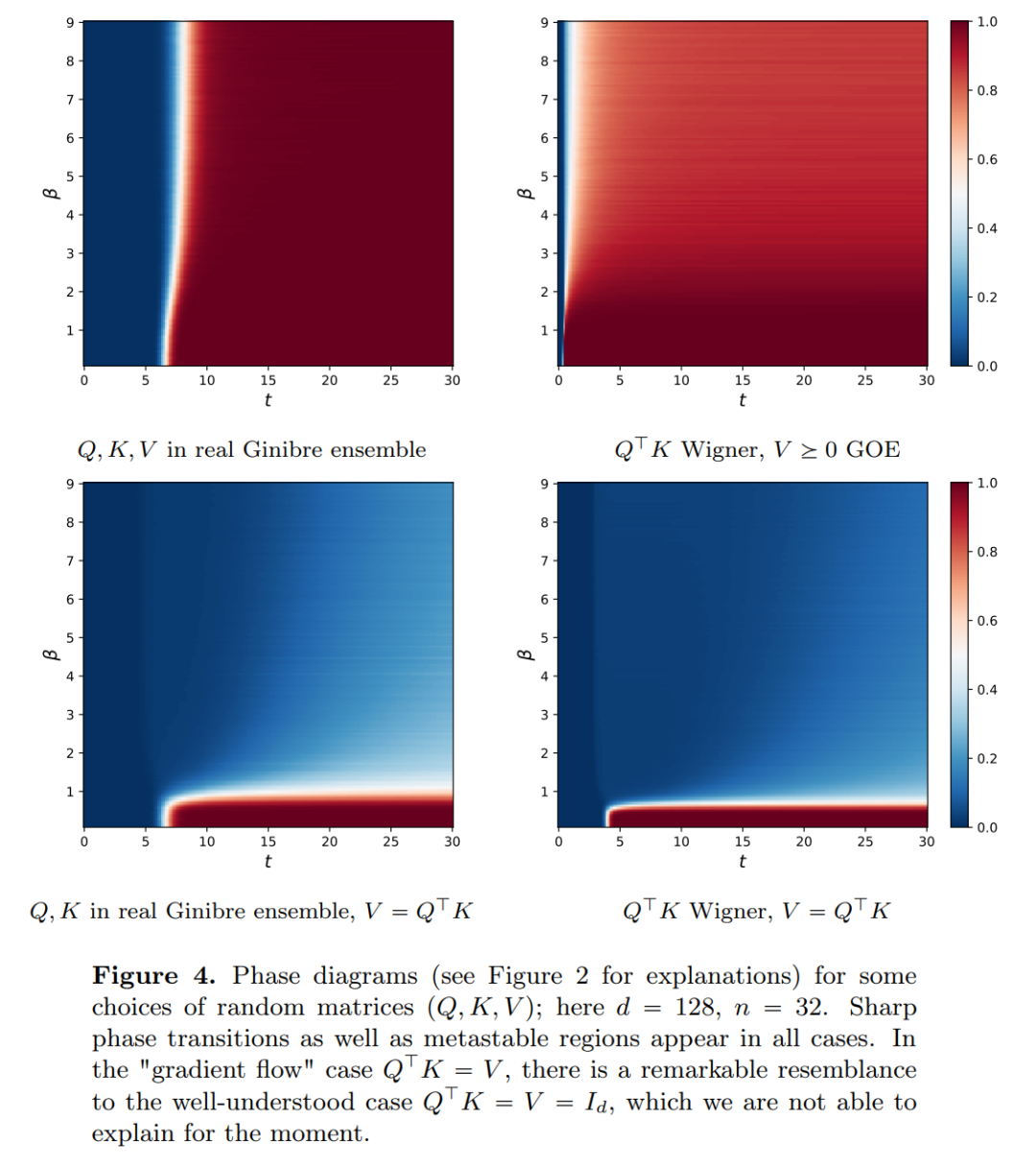
sous les contraintes des architectures DNN classiques. Les chercheurs ont découvert que les transformateurs sont en fait des mappages de flux sur  , c'est-à-dire des mappages entre des espaces de mesures de probabilité à d dimensions (l'espace des mesures de probabilité). Afin de mettre en œuvre cette cartographie de flux qui convertit entre les espaces métriques, les Transformers doivent établir un système de particules interagissant en champ moyen. Plus précisément, chaque particule (qui peut être comprise comme un jeton dans le contexte de l'apprentissage profond) suit le flux du champ vectoriel, et le flux dépend de la mesure empirique de toutes les particules. À leur tour, les équations déterminent l’évolution des mesures empiriques des particules, un processus qui peut durer longtemps et nécessiter une attention soutenue. Le principal constat des chercheurs est que les particules ont tendance à finir par s'agglutiner. Ce phénomène est particulièrement évident dans les tâches d'apprentissage telles que la dérivation unidirectionnelle (c'est-à-dire prédire le mot suivant dans une séquence). La métrique de sortie code la distribution de probabilité du jeton suivant, et un petit nombre de résultats possibles peuvent être filtrés en fonction des résultats de regroupement. Les résultats de recherche de cet article montrent que la distribution limite est en fait une masse ponctuelle et qu'il n'y a ni diversité ni caractère aléatoire, mais cela n'est pas cohérent avec les résultats d'observation réels. Cet apparent paradoxe est résolu par le fait que les particules existent dans des états variables pendant de longues périodes. Comme le montrent les figures 2 et 4, les transformateurs ont deux échelles de temps différentes : dans la première étape, tous les jetons forment rapidement plusieurs clusters, tandis que dans la deuxième étape (beaucoup plus lente que la première étape), pendant le processus de fusion par paires de clusters, tous les jetons finissent par s'effondrer en un seul point.
, c'est-à-dire des mappages entre des espaces de mesures de probabilité à d dimensions (l'espace des mesures de probabilité). Afin de mettre en œuvre cette cartographie de flux qui convertit entre les espaces métriques, les Transformers doivent établir un système de particules interagissant en champ moyen. Plus précisément, chaque particule (qui peut être comprise comme un jeton dans le contexte de l'apprentissage profond) suit le flux du champ vectoriel, et le flux dépend de la mesure empirique de toutes les particules. À leur tour, les équations déterminent l’évolution des mesures empiriques des particules, un processus qui peut durer longtemps et nécessiter une attention soutenue. Le principal constat des chercheurs est que les particules ont tendance à finir par s'agglutiner. Ce phénomène est particulièrement évident dans les tâches d'apprentissage telles que la dérivation unidirectionnelle (c'est-à-dire prédire le mot suivant dans une séquence). La métrique de sortie code la distribution de probabilité du jeton suivant, et un petit nombre de résultats possibles peuvent être filtrés en fonction des résultats de regroupement. Les résultats de recherche de cet article montrent que la distribution limite est en fait une masse ponctuelle et qu'il n'y a ni diversité ni caractère aléatoire, mais cela n'est pas cohérent avec les résultats d'observation réels. Cet apparent paradoxe est résolu par le fait que les particules existent dans des états variables pendant de longues périodes. Comme le montrent les figures 2 et 4, les transformateurs ont deux échelles de temps différentes : dans la première étape, tous les jetons forment rapidement plusieurs clusters, tandis que dans la deuxième étape (beaucoup plus lente que la première étape), pendant le processus de fusion par paires de clusters, tous les jetons finissent par s'effondrer en un seul point. 

L'objectif de cet article est double. D'une part, Cet article vise à fournir un cadre général et facile à comprendre pour étudier les Transformers d'un point de vue mathématique. En particulier, la structure de ces systèmes de particules en interaction permet aux chercheurs d’établir des liens concrets avec des sujets mathématiques établis, notamment les équations de transport non linéaires, les flux gradients de Wasserstein, les modèles de comportement collectif et les configurations optimales de points sur une sphère. D’autre part, cet article décrit plusieurs directions de recherche prometteuses, avec un accent particulier sur les phénomènes de clustering sur de longues périodes. Les principales mesures de résultats proposées par les chercheurs sont nouvelles et soulèvent également tout au long de l’article des questions ouvertes qu’ils jugent intéressantes. Les principales contributions de cet article sont divisées en trois parties. 
Partie 1 : Modélisation. Cet article définit un modèle idéal de l'architecture Transformer qui traite le nombre de couches comme une variable temporelle continue. Cette approche de l'abstraction n'est pas nouvelle et est similaire à l'approche adoptée par les architectures classiques telles que ResNets. Le modèle de cet article se concentre uniquement sur deux composants clés de l'architecture Transformer : le mécanisme d'auto-attention et la normalisation des couches. La normalisation des couches confine efficacement les particules à l'espace de la sphère unitaire  , tandis que le mécanisme d'auto-attention réalise un couplage non linéaire entre les particules grâce à des mesures empiriques. À son tour, la mesure empirique évolue selon une équation aux dérivées partielles de continuité. Cet article présente également un modèle alternatif plus simple et plus facile à utiliser pour l'attention personnelle, un flux gradient de Wasserstein d'une fonction énergétique. Il existe déjà des méthodes de recherche matures pour la configuration optimale des points sur la sphère de la fonction énergétique. Partie 2 : Clustering. Dans cette partie, les chercheurs proposent de nouveaux résultats mathématiques sur le clustering de jetons sur une période plus longue. Comme le montre le théorème 4.1, dans un espace de grande dimension, un groupe de n particules initialisées aléatoirement sur la boule unité se rassemblera en un point en
, tandis que le mécanisme d'auto-attention réalise un couplage non linéaire entre les particules grâce à des mesures empiriques. À son tour, la mesure empirique évolue selon une équation aux dérivées partielles de continuité. Cet article présente également un modèle alternatif plus simple et plus facile à utiliser pour l'attention personnelle, un flux gradient de Wasserstein d'une fonction énergétique. Il existe déjà des méthodes de recherche matures pour la configuration optimale des points sur la sphère de la fonction énergétique. Partie 2 : Clustering. Dans cette partie, les chercheurs proposent de nouveaux résultats mathématiques sur le clustering de jetons sur une période plus longue. Comme le montre le théorème 4.1, dans un espace de grande dimension, un groupe de n particules initialisées aléatoirement sur la boule unité se rassemblera en un point en  . La description précise par les chercheurs du taux de retrait des amas de particules complète ce résultat. Plus précisément, les chercheurs ont tracé des histogrammes des distances entre toutes les particules, ainsi que les moments où toutes les particules étaient sur le point de terminer leur regroupement (voir la section 4 de l'article original). Les chercheurs ont également obtenu des résultats de regroupement sans supposer une grande dimension d (voir la section 5 de l'article original). Partie 3 : Regarder vers l'avenir. Cet article propose des pistes potentielles de recherche future en posant principalement des questions sous la forme de questions ouvertes et en les étayant par des observations numériques. Les chercheurs se concentrent d’abord sur le cas de la dimension d = 2 (voir la section 6 de l’article original) et établissent le lien avec l’oscillateur de Kuramoto. Il est ensuite brièvement montré comment des problèmes difficiles liés à l'optimisation sphérique peuvent être résolus en apportant des modifications simples et naturelles au modèle (voir la section 7 de l'article original). Les chapitres suivants explorent les systèmes de particules en interaction qui permettent d'ajuster les paramètres de l'architecture du Transformer, ce qui pourra ultérieurement conduire à des applications pratiques.
. La description précise par les chercheurs du taux de retrait des amas de particules complète ce résultat. Plus précisément, les chercheurs ont tracé des histogrammes des distances entre toutes les particules, ainsi que les moments où toutes les particules étaient sur le point de terminer leur regroupement (voir la section 4 de l'article original). Les chercheurs ont également obtenu des résultats de regroupement sans supposer une grande dimension d (voir la section 5 de l'article original). Partie 3 : Regarder vers l'avenir. Cet article propose des pistes potentielles de recherche future en posant principalement des questions sous la forme de questions ouvertes et en les étayant par des observations numériques. Les chercheurs se concentrent d’abord sur le cas de la dimension d = 2 (voir la section 6 de l’article original) et établissent le lien avec l’oscillateur de Kuramoto. Il est ensuite brièvement montré comment des problèmes difficiles liés à l'optimisation sphérique peuvent être résolus en apportant des modifications simples et naturelles au modèle (voir la section 7 de l'article original). Les chapitres suivants explorent les systèmes de particules en interaction qui permettent d'ajuster les paramètres de l'architecture du Transformer, ce qui pourra ultérieurement conduire à des applications pratiques. Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

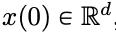 évoluera en fonction du champ de vitesse variable dans le temps donné
évoluera en fonction du champ de vitesse variable dans le temps donné 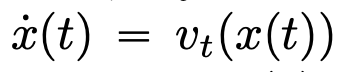 sur l'intervalle de temps (0, T). Par conséquent, le DNN peut être considéré comme une Flow Map
sur l'intervalle de temps (0, T). Par conséquent, le DNN peut être considéré comme une Flow Map 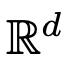 d’un
d’un  à un autre
à un autre 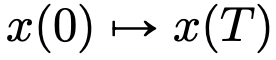 . Il existe une forte similitude entre les cartes de flux même dans les champs de vitesse
. Il existe une forte similitude entre les cartes de flux même dans les champs de vitesse 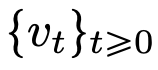 sous les contraintes des architectures DNN classiques.
sous les contraintes des architectures DNN classiques. 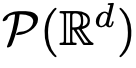 , c'est-à-dire des mappages entre des espaces de mesures de probabilité à d dimensions (l'espace des mesures de probabilité). Afin de mettre en œuvre cette cartographie de flux qui convertit entre les espaces métriques, les Transformers doivent établir un système de particules interagissant en champ moyen.
, c'est-à-dire des mappages entre des espaces de mesures de probabilité à d dimensions (l'espace des mesures de probabilité). Afin de mettre en œuvre cette cartographie de flux qui convertit entre les espaces métriques, les Transformers doivent établir un système de particules interagissant en champ moyen. 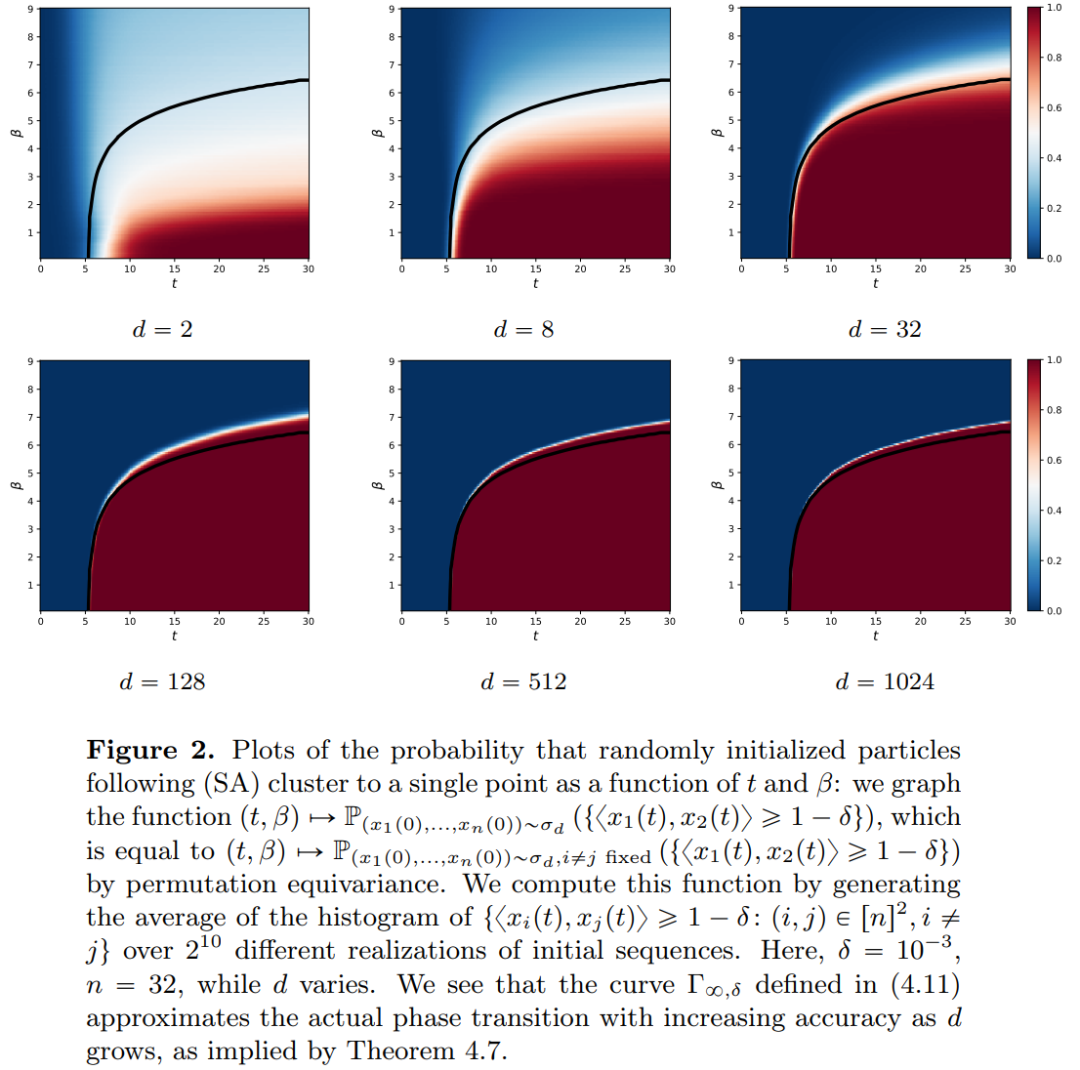

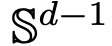 , tandis que le mécanisme d'auto-attention réalise un couplage non linéaire entre les particules grâce à des mesures empiriques. À son tour, la mesure empirique évolue selon une équation aux dérivées partielles de continuité. Cet article présente également un modèle alternatif plus simple et plus facile à utiliser pour l'attention personnelle, un flux gradient de Wasserstein d'une fonction énergétique. Il existe déjà des méthodes de recherche matures pour la configuration optimale des points sur la sphère de la fonction énergétique.
, tandis que le mécanisme d'auto-attention réalise un couplage non linéaire entre les particules grâce à des mesures empiriques. À son tour, la mesure empirique évolue selon une équation aux dérivées partielles de continuité. Cet article présente également un modèle alternatif plus simple et plus facile à utiliser pour l'attention personnelle, un flux gradient de Wasserstein d'une fonction énergétique. Il existe déjà des méthodes de recherche matures pour la configuration optimale des points sur la sphère de la fonction énergétique. 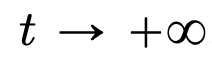 . La description précise par les chercheurs du taux de retrait des amas de particules complète ce résultat. Plus précisément, les chercheurs ont tracé des histogrammes des distances entre toutes les particules, ainsi que les moments où toutes les particules étaient sur le point de terminer leur regroupement (voir la section 4 de l'article original). Les chercheurs ont également obtenu des résultats de regroupement sans supposer une grande dimension d (voir la section 5 de l'article original).
. La description précise par les chercheurs du taux de retrait des amas de particules complète ce résultat. Plus précisément, les chercheurs ont tracé des histogrammes des distances entre toutes les particules, ainsi que les moments où toutes les particules étaient sur le point de terminer leur regroupement (voir la section 4 de l'article original). Les chercheurs ont également obtenu des résultats de regroupement sans supposer une grande dimension d (voir la section 5 de l'article original). 
