Maison >tutoriels informatiques >connaissances en informatique >Implémentez la fonction power de manière récursive en langage C et appelez-la dans la fonction principale
Implémentez la fonction power de manière récursive en langage C et appelez-la dans la fonction principale
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2024-01-09 09:54:321600parcourir
Question en langage C : utilisez la méthode récursive pour écrire une fonction de puissance et appelez-la dans la fonction principale en utilisant le langage C La valeur de
/*x^n doit être inférieure à 32767, sinon le résultat sera un nombre négatif. En effet, la plage de valeurs du type int est limitée. Les fonctions pow normales utilisent généralement des types float ou double, et les paramètres doivent également être des types float ou double. */
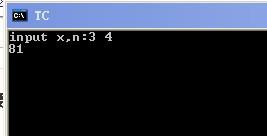
#inclure
int puissance(int x,int n)
{
si (n>1)
{
retour x*puissance(x,n-1);
}
autre
{
si (n>0)
retour x;
autre
retour 1;
}
}
void main()
{
int x,n;
printf("entrée x,n:");
scanf("%d%d",&x,&n);
printf("%d",puissance(x,n));
getch();
clrscr();
}
Langage C sur la récursivité des fonctions
Votre programme récursif est erroné. Je vais en transférer un correct avec explication. Vous pouvez y jeter un œil.
Récursion et appel de fonctions de langage
1. Contenu de base :
Les fonctions en langage C peuvent être appelées de manière récursive, c'est-à-dire qu'elles peuvent être appelées directement (récursion simple) ou indirectement (récursion indirecte).
Points :
1. Les fonctions du langage C peuvent être appelées de manière récursive.
2. Il peut être appelé directement ou indirectement. Actuellement, seuls les appels récursifs directs sont discutés.
2. Condition de récursion
Utiliser des méthodes récursives pour résoudre des problèmes doit répondre aux trois conditions suivantes :
1. Le problème à résoudre peut être transformé en un nouveau problème, et la solution à ce nouveau problème est toujours la même que la solution originale, sauf que les objets en cours de traitement augmentent ou diminuent régulièrement.
Remarque : La méthode pour résoudre le problème est la même. Les paramètres d'appel de la fonction sont différents à chaque fois (incrémentation ou décrémentation régulière). S'il n'y a pas de modèle, l'appel récursif ne peut pas être appliqué.
2. Ce processus de transformation peut être appliqué pour résoudre le problème.
Remarque : l'utilisation d'autres méthodes est lourde ou difficile à résoudre, mais l'utilisation de méthodes récursives peut bien résoudre le problème.
3. Il doit y avoir une condition claire pour mettre fin à la récursion.
Remarque : assurez-vous de mettre fin à l'appel récursif à l'endroit approprié. Sinon, le système pourrait planter.
3. Exemple récursif
Exemple : Utilisation de la méthode récursive n !
Quand n>1, n! Le problème peut se transformer en n*(n-1) ! de nouvelles questions.
Par exemple n=5 :
Première partie : 5*4*3*2*1 n*(n-1) !
Partie 2 : 4*3*2*1 (n-1)*(n-2) !
Partie 3 : 3*2*1 (n-2)(n-3) !
Partie 4 : 2*1 (n-3)(n-4) !
Partie 5 : 1 (n-5) ! 5-5=0, obtenez la valeur 1, terminez la récursion.
Programme source :
fac(int n)
{int t;
if(n==1)||(n==0) renvoie 1;
autre
{t=n*fac(n-1);
retourner;
}
}
principale( )
{int m,y;
printf("Entrez m:");
scanf("%d",&m);
if(m
autre
{y=fac(m);
printf("n%d! =%d n",m,y);
}
}
4. Explication de la récursion
1. Lorsqu'une fonction s'appelle elle-même, le système conservera automatiquement temporairement les variables et les paramètres formels actuels dans la fonction. Lors d'un nouveau cycle d'appel, le système ouvrira un autre emplacement pour les variables et les paramètres formels utilisés par la fonction nouvellement appelée. . unité de stockage (espace mémoire). Les variables utilisées dans chaque appel de fonction se trouvent dans des espaces mémoire différents.
2. Plus il y a de niveaux d'appels récursifs, plus il y a d'unités de stockage occupées par des variables du même nom. Il est important de se rappeler qu’à chaque fois qu’une fonction est appelée, le système ouvrira un nouvel espace mémoire pour les variables de la fonction.
3. Lorsque la fonction appelée cette fois se termine, le système libérera l'espace mémoire occupé par cet appel. Le flux du programme revient au point d'appel de la couche précédente et obtient en même temps les données de l'espace mémoire occupé par les variables et les paramètres formels de la fonction lors de l'entrée dans cette couche.
4. Tous les problèmes récursifs peuvent être résolus avec des méthodes non récursives, mais pour certains problèmes récursifs plus complexes, l'utilisation de méthodes non récursives rend souvent le programme très compliqué et difficile à lire. L'appel récursif de fonctions est très utile pour résoudre de tels problèmes. . Cela peut rendre le programme concis et clair avec une meilleure lisibilité ; cependant, pendant le processus d'appel récursif, le système doit ouvrir de l'espace mémoire pour les variables dans chaque couche d'appels, mémoriser les points de retour après chaque couche d'appels et a besoin. pour ajouter beaucoup de surcharge supplémentaire, de sorte que les appels récursifs aux fonctions réduisent généralement l'efficacité d'exécution du programme.
5. Procédure
fac(int n) /*Utiliser des paramètres différents pour chaque appel*/
{ int t; /* Chaque appel ouvrira un espace mémoire différent pour la variable t*/
if(n==1)||(n==0) /*Renvoyer 1 lorsque ces conditions sont remplies */
retour 1;
autre
{ t=n*fac(n-1); /*Chaque fois que le programme s'exécute ici, cette fonction sera à nouveau appelée avec n-1 comme paramètre*/
.return t; /*Exécuter ici uniquement lorsque tous les processus appelés dans la phrase précédente sont terminés. */
}
}
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Comprendre la fonction du masquage de sous-réseau et son importance dans la planification du réseau
- Analyse approfondie des fonctions et principes des masques de sous-réseau
- Fichier TmP : comment ouvrir et inspecter son contenu ?
- Quelles sont les fonctions et fonctions des fichiers TmP ?
- Quel type de format de fichier est un fichier TmP ?

