Maison >tutoriels informatiques >connaissances en informatique >Explication détaillée de la méthode de mise en œuvre de la méthode d'itération des équations non linéaires dans Matlab
Explication détaillée de la méthode de mise en œuvre de la méthode d'itération des équations non linéaires dans Matlab
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2024-01-08 16:06:351005parcourir
Description détaillée de l'implémentation Matlab de la méthode d'itération du système d'équations non linéaires
Méthode d'itération de Newton :
fonction[x0,n]=newton(fx,dfx,x0,tol,N)
Méthode d'itération% Newton
% Le premier paramètre fx est l'expression de fonction souhaitée concernant la variable x.
% Le deuxième paramètre dfx est la dérivée première de fx.
% x0 est la valeur initiale de l'itération.
% tol est la limite d'erreur d'itération.
% N Nombre maximum d'itérations.
x=x0;f0=eval(fx);df0=eval(dfx);
n=0;
disp('[ n xn xn+1 delta ]');
pendant que n
x1=x0-f0/df0;
x=x1;f1=eval(fx);df1=eval(dfx);
delta=abs(x0-x1);
% X=[n,x0,x1,delta];
disp(X); % est utilisé pour afficher les résultats intermédiaires
si delta fprintf('Calcul d'itération réussi') retour autre n=n+1; x0=x1;f0=f1;df0=df1; fin fin si n==N+1 fprintf('Le calcul de l'itération a échoué') fin Les deux autres peuvent être légèrement modifiés en fonction de cela. Je vous donne une version complète : % Méthode de Newton pour résoudre des équations non linéaires fonction principale() clc ; tout effacer ; f = @(x)log(x+sin(x)); % fonction de test df = @(x)(1+cos(x))/(x+sin(x)); % fonction dérivée x0 = 0,1 ; % valeur initiale de l'itération x = TestNewton(f, df, x0) % Méthode de Newton fonction x = TestNewton(fname, dfname, x0, e, N) % Objectif : méthode d'itération de Newton pour résoudre l'équation non linéaire f(x)=0 % fname et dfname représentent respectivement le handle de fonction M ou l'expression de fonction intégrée de f(x) et sa fonction dérivée % x0 est la valeur initiale de l'itération, e est la précision (valeur par défaut 1e-7) % x renvoie la solution numérique et affiche le processus de calcul. Définissez la limite supérieure du nombre d'itérations N pour éviter la divergence (par défaut 500 fois) % paramètres d'entrée si nargin
N = 500; fin si nargin
e = 1e-7; fin x = x0 ; % valeur initiale x0 = x+2*e; % flottant k = 0 ; % nombre de pas fprintf('x[%d]=%12.9fn', k, x) % informations d'impression while abs(x0-x)>e & k k = k+1 ; % enregistre le nombre de pas x0 = x; % mise à jour x(k) x = x0 - feval(fname,x0)/feval(dfname,x0); % mise à jour x(k+1) fprintf('x[%d]=%12.9fn', k, x) % informations d'impression fin si k == N fprintf('Le nombre maximum d'itérations a été atteint'); % itération terminée fin Résultat : Programme MATLAB pour utiliser l'itération de Newton pour résoudre des équations non linéaires
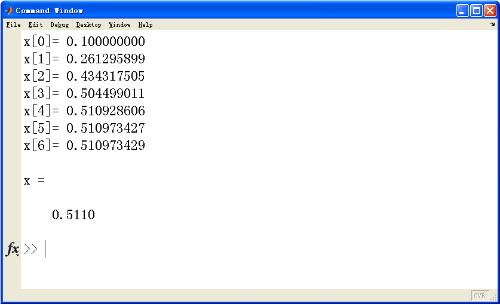
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Comprendre la fonction du masquage de sous-réseau et son importance dans la planification du réseau
- Analyse approfondie des fonctions et principes des masques de sous-réseau
- Fichier TmP : comment ouvrir et inspecter son contenu ?
- Quelles sont les fonctions et fonctions des fichiers TmP ?
- Quel type de format de fichier est un fichier TmP ?

