11 distributions de base que les data scientists utilisent 95 % du temps

Suite au dernier inventaire des "11 graphiques de base utilisés par les data scientists 95% du temps", nous vous présenterons aujourd'hui 11 distributions de base que les data scientists utilisent 95% du temps. La maîtrise de ces distributions nous aide à comprendre plus profondément la nature des données et à faire des inférences et des prédictions plus précises lors de l'analyse des données et de la prise de décision.

1. Distribution normale

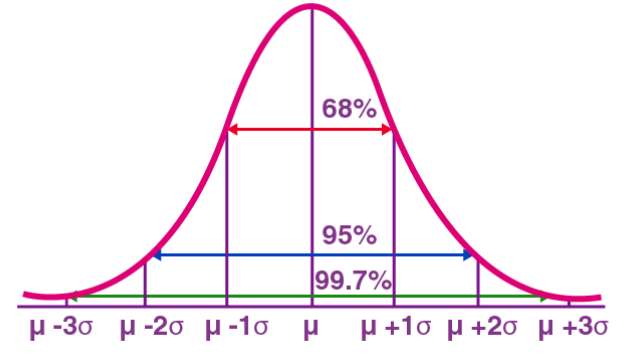
La distribution normale, également connue sous le nom de distribution gaussienne, est une distribution de probabilité continue. Il présente une courbe symétrique en forme de cloche avec la moyenne (μ) comme centre et l'écart type (σ) comme largeur. La distribution normale a une valeur d'application importante dans de nombreux domaines tels que les statistiques, la théorie des probabilités et l'ingénierie.

La fonction de densité de probabilité de la distribution normale peut être exprimée comme suit :

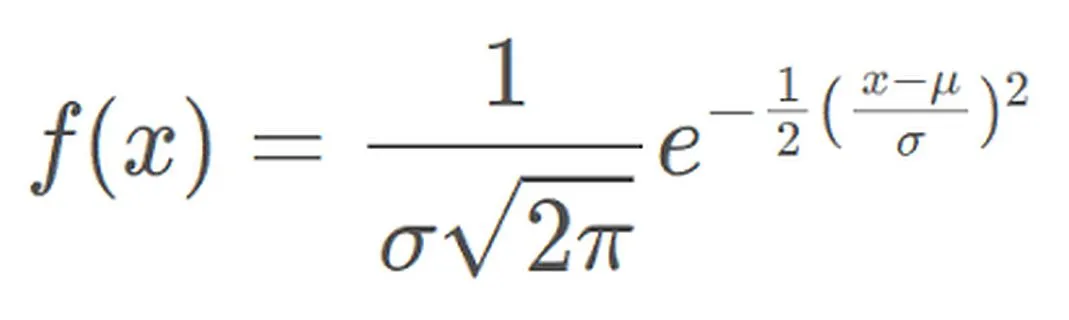
La fonction de densité de probabilité représente la densité de probabilité des valeurs d'une variable aléatoire normalement distribuée dans l'intervalle unitaire près d'une valeur donnée X. Parmi eux, μ représente la moyenne et σ représente l'écart type. La distribution normale est largement utilisée dans la pratique. Par exemple, la distribution de la taille et du poids humains se rapproche d’une distribution normale. En outre, les résultats des tests sont souvent distribués normalement, avec moins de personnes ayant des scores élevés et faibles et davantage de personnes ayant des scores moyens. Ce modèle de distribution a une valeur d'application importante dans de nombreux domaines

2. La distribution de Bernoulli

La distribution de Bernoulli (distribution de Bernoulli) est une distribution de probabilité discrète utilisée pour décrire un seul événement avec seulement deux résultats possibles. Les essais de Bernoulli peuvent être pile ou face, succès ou échec, oui ou non, etc. Par exemple, lancer une pièce de monnaie, tester si un produit est qualifié, si quelqu'un achète un certain produit, etc.

La fonction de masse de probabilité de la distribution de Bernoulli est :

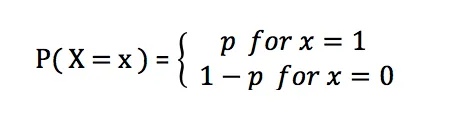Dans la distribution de Bernoulli, p représente la probabilité de succès et sa valeur varie de 0 à 1. Lorsque p est égal à 0,5, la distribution de Bernoulli se rapproche d'une distribution uniforme

Application de la distribution de Bernoulli en pratique : Par exemple, la distribution binomiale est n expériences répétées indépendantes de la distribution de Bernoulli.

3. Distribution binomiale

La distribution binomiale (distribution binomiale) est une distribution de probabilité discrète utilisée pour décrire la distribution de probabilité du nombre de réussites dans n expériences répétées indépendantes. Chaque essai n'a que deux résultats possibles : le succès (enregistré comme 1) ou l'échec (enregistré comme 0). La probabilité de succès est p et la probabilité d’échec est 1-p.

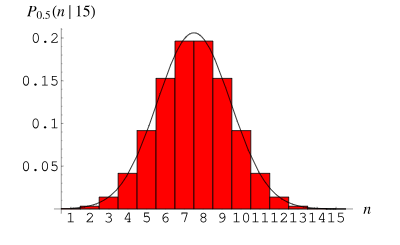La fonction de masse de probabilité de la distribution binomiale peut être exprimée comme suit :

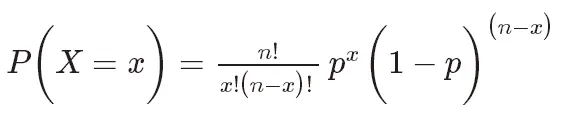où, P(X=k) représente la probabilité de k fois de réussite,

est le nombre de combinaisons, indiquant la sélection de k à partir de n essais Le nombre de combinaisons réussies. p est la probabilité de succès, allant de 0 à 1. n est le nombre d'essais.

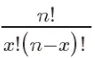La distribution binomiale est largement utilisée dans la pratique. Par exemple, dans la recherche médicale, nous pouvons utiliser la distribution binomiale pour calculer le taux de réussite d’un patient recevant un certain traitement. Dans le domaine de l'ingénierie, on peut utiliser la distribution binomiale pour évaluer le taux de qualification d'un produit au cours du processus de production. Ce sont des exemples importants de distribution binomiale dans des applications pratiques

4. La distribution de Poisson

La distribution de Poisson (distribution de Poisson) est une distribution de probabilité discrète utilisée pour décrire le nombre d'événements qui se produisent dans une période de temps fixe. La distribution de Poisson convient aux situations où les événements sont indépendants et se produisent à un rythme moyen constant.

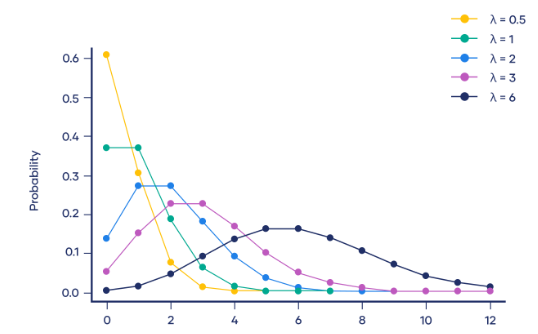La fonction de densité de probabilité de la distribution de Poisson est :

Ici, P(X=k) représente la probabilité qu'un événement se produise k fois dans une période de temps fixe, et λ représente le taux d'occurrence moyen d'un événement, qui est le nombre moyen d'événements se produisant par unité de temps. e est une constante naturelle, approximativement égale à 2,718. k représente le nombre d'événements qui se produisent. La distribution de Poisson est largement utilisée dans la pratique. Par exemple, dans un centre d'appels, le nombre d'appels par minute peut être considéré comme une distribution de Poisson, où le nombre moyen d'appels par minute est λ

.

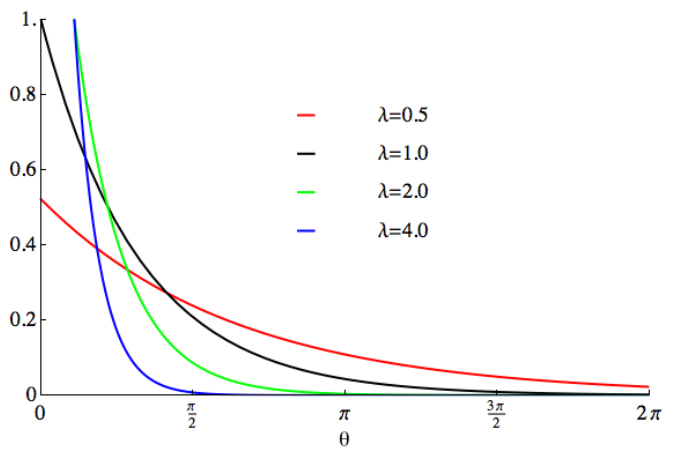
5. Distribution exponentielle

La distribution exponentielle (distribution exponentielle) est une distribution de probabilité continue utilisée pour décrire la probabilité qu'un événement se produise dans un temps fixe. La distribution exponentielle convient aux situations dans lesquelles les événements sont indépendants les uns des autres et se produisent à un rythme moyen constant.

La fonction de densité de probabilité de la distribution exponentielle est :

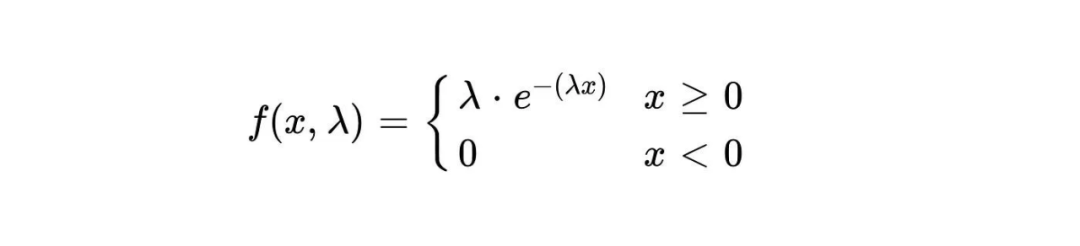La densité de probabilité d'un événement se produisant dans un temps donné x est représentée par f(x,λ). λ représente le taux d'occurrence moyen des événements, c'est-à-dire le nombre moyen d'événements se produisant par unité de temps. e est une constante naturelle, approximativement égale à 2,718

La distribution exponentielle a de nombreuses applications dans la vie réelle. Par exemple, dans la désintégration radioactive, les temps de désintégration des noyaux radioactifs peuvent être considérés comme distribués de manière exponentielle. Cela signifie que la distribution de probabilité des temps de décroissance suit une fonction exponentielle. Le temps de décroissance moyen correspond au paramètre λ de la fonction exponentielle

6. Distribution gamma

La distribution gamma est une distribution de probabilité continue utilisée pour décrire la probabilité qu'un événement se produise dans un temps donné. Cela s'applique à la situation où les événements sont indépendants les uns des autres et le taux d'occurrence moyen est toujours constant. La fonction de densité de probabilité de la distribution gamma est :

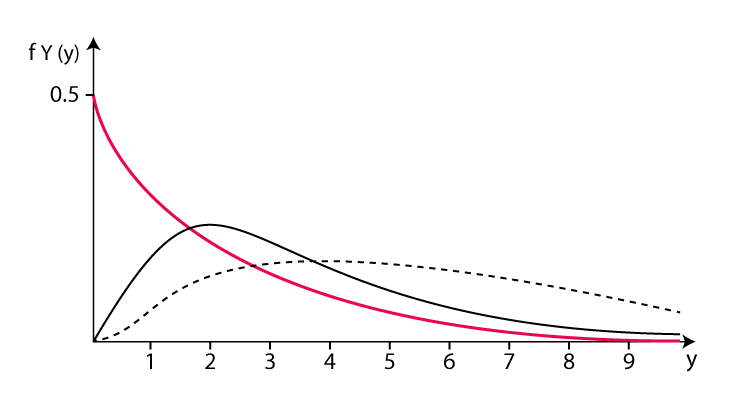où f(x) représente le temps x à un instant précis. densité de probabilité des événements internes. α et β sont les paramètres de forme et les paramètres de taux de la distribution gamma. α est utilisé pour déterminer la forme de la distribution gamma et sa valeur va de 0 à l’infini positif. β représente le taux d'occurrence moyen des événements, c'est-à-dire le nombre moyen d'événements se produisant par unité de temps, et la plage de valeurs va de 0 à l'infini positif. e est une constante naturelle, approximativement égale à 2,718. Applications pratiques de la distribution gamma : Par exemple, désintégration radioactive : Dans la désintégration radioactive, le temps nécessaire à la désintégration des noyaux radioactifs peut être considéré comme une distribution gamma, et le temps de désintégration moyen est β/. α.

7. Distribution bêta

La distribution bêta est une distribution de probabilité continue qui est utilisée pour décrire la distribution de probabilité du nombre de succès dans un ensemble de valeurs. Il comporte deux paramètres, représentant la valeur attendue (moyenne) et l'écart type (écart type) de la probabilité de succès.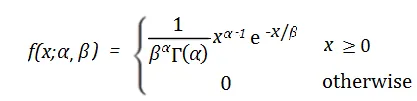

La fonction de densité de probabilité de la distribution bêta est la suivante :

En cela, x représente le nombre de succès, α et β représentent respectivement les paramètres de forme de la distribution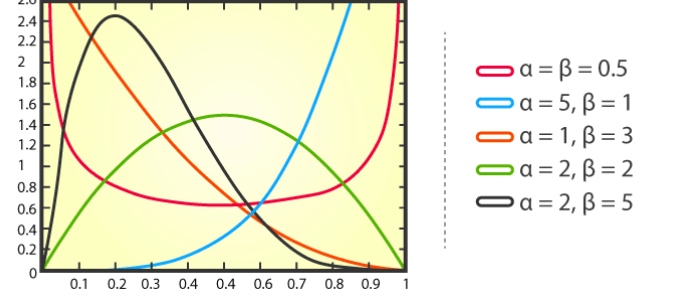

La distribution bêta a des applications dans de nombreux problèmes pratiques. Par exemple, dans le domaine de l’édition génétique, les chercheurs peuvent utiliser une distribution bêta pour prédire la probabilité qu’une technologie d’édition génétique parvienne à modifier un certain site cible. Dans le domaine financier, la distribution bêta peut être utilisée pour décrire la volatilité des prix des actifs ou pour calculer le rendement attendu d'un portefeuille d'investissement

8 Distribution uniforme

La distribution uniforme est une distribution de probabilité utilisée pour décrire un ensemble. de valeurs dans un certain uniformément réparties dans l'intervalle. Il existe deux types de distributions uniformes : la distribution uniforme discrète et la distribution uniforme continue.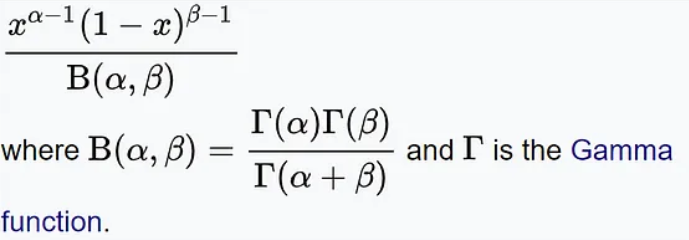

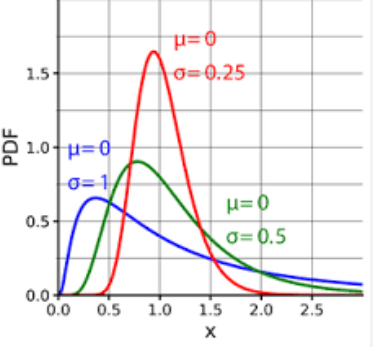
Distribution uniforme discrète : Lorsqu'une variable aléatoire discrète Elle obéit à une distribution uniforme discrète. Distribution uniforme continue : lorsque la fonction de densité de probabilité d'une variable aléatoire continue X est f(x) = 1/(b-a), nous disons que la caractéristique d'une distribution uniforme est que dans un intervalle donné, chaque valeur a une chance égale de se produisant. Par exemple, si vous lancez une pièce équitable, la probabilité d’obtenir pile ou face est de 1/2, ce qui est une distribution uniforme.

9. Distribution log-normale

La distribution log-normale (Distribution Log-normale) est une distribution de probabilité continue, qui est caractérisée par le logarithme de la variable aléatoire obéissant à la distribution normale. En d’autres termes, si le logarithme ln(X) d’une variable aléatoire X obéit à la distribution normale, alors la variable aléatoire X obéit à la distribution lognormale.

La fonction de densité de probabilité de la distribution lognormale peut être exprimée comme suit :

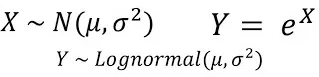
où μ est la moyenne de la distribution lognormale et σ est l'écart type de la distribution lognormale.

La distribution lognormale revêt une grande importance dans de nombreuses applications pratiques, telles que la finance (cours des actions, rendements, etc.), la biologie (taux de croissance, etc.), l'économie (dépenses de consommation, etc.), etc.

10. Distribution T

La distribution T est une distribution de probabilité continue, qui est principalement utilisée pour décrire la distribution de la moyenne dans le cas de petits échantillons. La distribution t est similaire à la distribution normale, mais sa queue peut s'étendre vers la gauche et la droite, en fonction du degré de liberté (k). La distribution t est largement utilisée dans l'inférence statistique, comme dans les tests d'hypothèses pour évaluer la différence significative entre la moyenne de l'échantillon et la moyenne de la population.

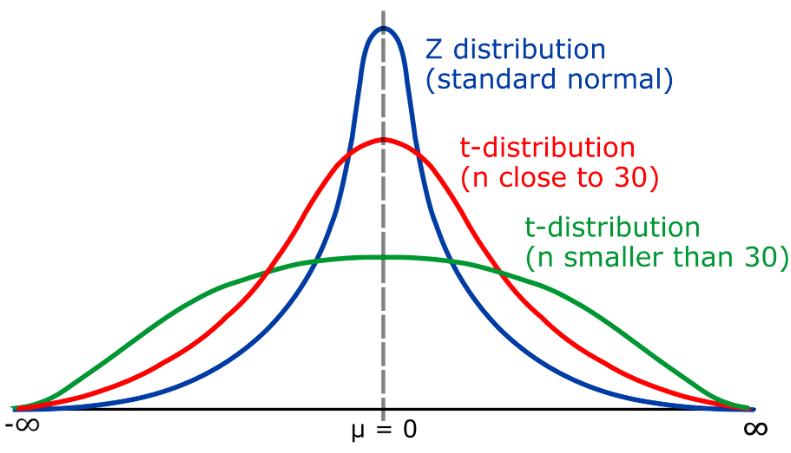
L'espérance et la variance de la distribution t sont les suivantes :

E(t)=0

Le contenu à réécrire est : Var(t)=k/(k-1)

Les degrés de la distribution de liberté de t (k) représente la relation entre la taille de l'échantillon (n) et l'écart type de la population. Lorsque k > 30, la distribution t est proche de la distribution normale ; lorsque k est proche de 1, la distribution t devient la distribution de Cauchy (distribution de Cauchy)

Dans les applications pratiques, lorsque la taille de l'échantillon est grande (n>30) , cela peut Le test d'hypothèse est effectué en utilisant la distribution normale. Dans ce cas, la statistique z peut être utilisée pour établir un intervalle de confiance. Cependant, lorsque la taille de l'échantillon est petite (n

11. Distribution de Weibull

La distribution de Weibull (distribution de Weibull) est une distribution de probabilité continue.

La fonction de densité de probabilité de la distribution de Weibull est :

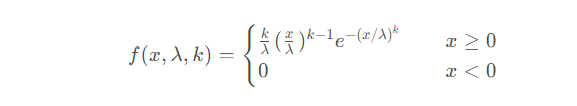
Dans la distribution de Weibull, x est considéré comme une variable aléatoire, λ est appelé le paramètre d'échelle (échelle) et k est le paramètre de forme (forme). En ce qui concerne la distribution de Weber, lorsque k est égal à 1, il s'agit d'une distribution exponentielle. Si λ est égal à 1, c'est la distribution de Weber minimisée

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!