Maison >Périphériques technologiques >IA >Algorithmes de régression couramment utilisés et leurs caractéristiques dans les applications d'apprentissage automatique
Algorithmes de régression couramment utilisés et leurs caractéristiques dans les applications d'apprentissage automatique
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-11-29 17:29:261006parcourir
La régression est l'un des outils les plus puissants en statistique. Les algorithmes d'apprentissage supervisé du machine learning sont divisés en deux types : les algorithmes de classification et les algorithmes de régression. L'algorithme de régression est utilisé pour la prédiction de distribution continue et peut prédire des données continues plutôt que de simples étiquettes de catégories discrètes.
L'analyse de régression est largement utilisée dans le domaine de l'apprentissage automatique, comme la prévision des ventes de produits, du flux de trafic, des prix des logements, des conditions météorologiques, etc. L'algorithme de régression est un algorithme d'apprentissage automatique couramment utilisé pour établir la relation entre les indépendants relation entre la variable X et la variable dépendante Y. Du point de vue de l'apprentissage automatique, il est utilisé pour créer un modèle d'algorithme (fonction) afin d'obtenir la relation de mappage entre l'attribut X et l'étiquette Y. Pendant le processus d'apprentissage, l'algorithme essaie de trouver la meilleure relation de paramètres afin que l'ajustement soit le meilleur Dans l'algorithme de régression, le résultat final de l'algorithme (fonction) est une valeur de données continue. La valeur d'entrée (valeur d'attribut) est un attribut/vecteur numérique à dimensions DCertains algorithmes de régression couramment utilisés incluent la régression linéaire, la régression polynomiale, la régression d'arbre de décision, la régression Ridge, la régression Lasso, la régression ElasticNet, etc.Cet article sera présenter quelques algorithmes de régression courants et leurs caractéristiques respectives régression arborescente
- Random La forêt est de retour
- LASSO est de retour
- Ridge est de retour
- ElasticNet est de retour
- X GBoost est de retour
- Local Weighted Régression linéaire
- Premièrement, la régression linéaireLa régression linéaire est souvent le premier algorithme que les gens découvrent sur l'apprentissage automatique et la science des données. La régression linéaire est un modèle linéaire qui suppose une relation linéaire entre une variable d'entrée (X) et une seule variable de sortie (y). De manière générale, il existe deux situations :
- La régression linéaire univariée est une méthode de modélisation utilisée pour analyser la relation entre une variable d'entrée unique (c'est-à-dire une variable de caractéristique unique) et une variable de sortie unique.
- Régression linéaire multivariée (également appelée régression linéaire multiple) : elle modélise la relation entre plusieurs variables d'entrée (plusieurs variables de caractéristiques) et une seule variable de sortie. Quelques points clés sur la régression linéaire :
- Rapide et facile à modéliser
Elle est particulièrement utile lorsque la relation que vous souhaitez modéliser n'est pas très complexe et que vous n'avez pas beaucoup de données.
Compréhension et explication très intuitives.
Il est très sensible aux valeurs aberrantes.
2. Régression polynomiale
Lorsque nous souhaitons créer un modèle pour des données séparables non linéaires, la régression polynomiale est l'un des choix les plus populaires. Elle est similaire à la régression linéaire mais utilise la relation entre les variables X et y pour trouver la meilleure façon de tracer une courbe qui correspond aux points de données.
- Quelques points clés sur la régression polynomiale :
- est capable de modéliser des données séparables non linéaires ; En général, il est plus flexible et permet de modéliser des relations assez complexes.
- Contrôle total sur la modélisation des variables de caractéristiques (exposants à définir).
- Nécessite une conception soignée. Une certaine connaissance des données est nécessaire pour sélectionner le meilleur indice.
Si l'index n'est pas choisi correctement, il est facile de le surajuster.
3. Régression des machines à vecteurs de support
Les machines à vecteurs de support sont bien connues dans les problèmes de classification. L'utilisation de SVM en régression est appelée Support Vector Regression (SVR). Scikit-learn a cette méthode intégrée à SVR().
- Quelques points clés sur la régression vectorielle de support :
- Elle est robuste aux valeurs aberrantes et efficace dans un espace de grande dimension
- Elle possède une excellente capacité de généralisation (capacité de s'adapter correctement à de nouveaux données)
- Si le nombre de caractéristiques est beaucoup plus grand que le nombre d'échantillons, il est facile de surajuster
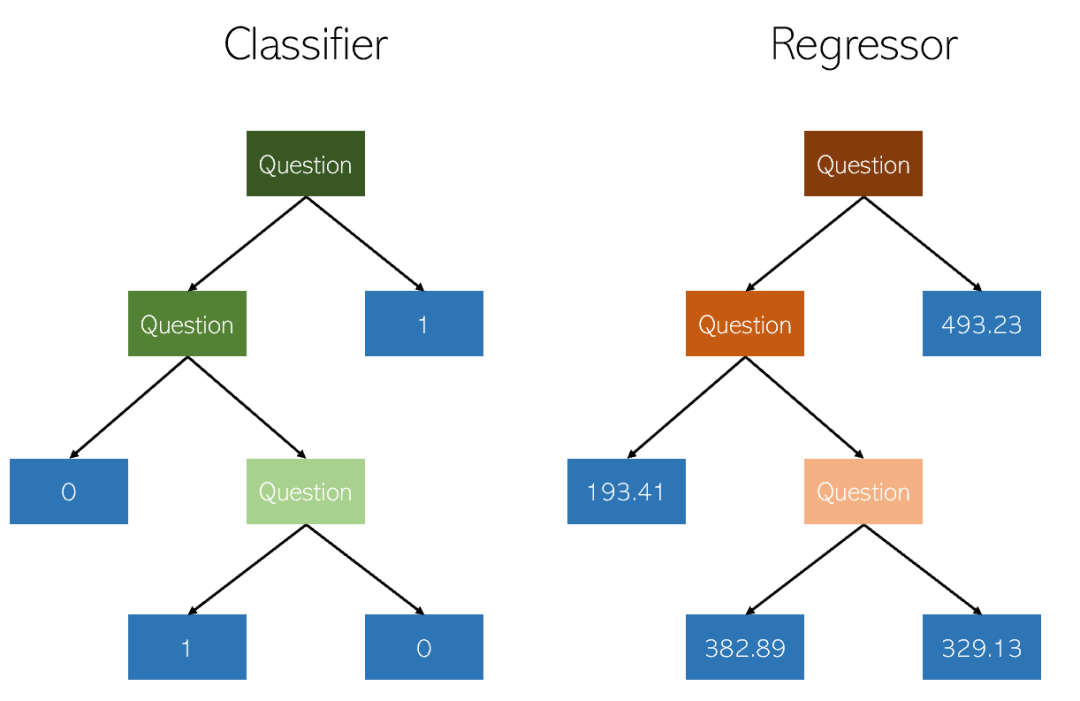
4. Régression de l'arbre de décision
L'arbre de décision est une méthode utilisée pour la classification et la régression non paramétrique méthode d'apprentissage supervisé. L'objectif est de créer un modèle qui prédit la valeur d'une variable cible en apprenant des règles de décision simples déduites des caractéristiques des données. Un arbre peut être considéré comme une approximation constante par morceaux.
Quelques points clés sur les arbres de décision :
- Facile à comprendre et à expliquer. Les arbres peuvent être visualisés.
- S'applique à la fois aux valeurs catégorielles et continues
- Le coût d'utilisation de DT (c'est-à-dire les données de prédiction) est logarithmique par rapport au nombre de points de données utilisés pour entraîner l'arbre
- Les prédictions des arbres de décision ne sont ni fluides ni continue (Comme le montre la figure ci-dessus, il s'agit d'une approximation constante par morceaux)
5. Régression de forêt aléatoire
La régression de forêt aléatoire et la régression d'arbre de décision sont fondamentalement très similaires. Il s'agit d'un méta-estimateur qui peut ajuster plusieurs arbres de décision sur divers sous-échantillons de l'ensemble de données et les moyenner pour améliorer la précision des prédictions et contrôler le surajustement
Régresseur de forêt aléatoire dans les problèmes de régression Les performances peuvent être meilleures ou pires que celles des arbres de décision (bien que souvent meilleur dans les problèmes de classification) en raison de subtils compromis de surajustement et de sous-ajustement inhérents à l'algorithme de construction d'arbres
À propos des forêts aléatoires Quelques points de régression :
- Réduisez le surajustement dans les arbres de décision et améliorez la précision.
- Cela fonctionne également pour les valeurs catégorielles et continues.
- Nécessite beaucoup de puissance de calcul et de ressources car il s'adapte à de nombreux arbres de décision pour combiner leurs résultats.
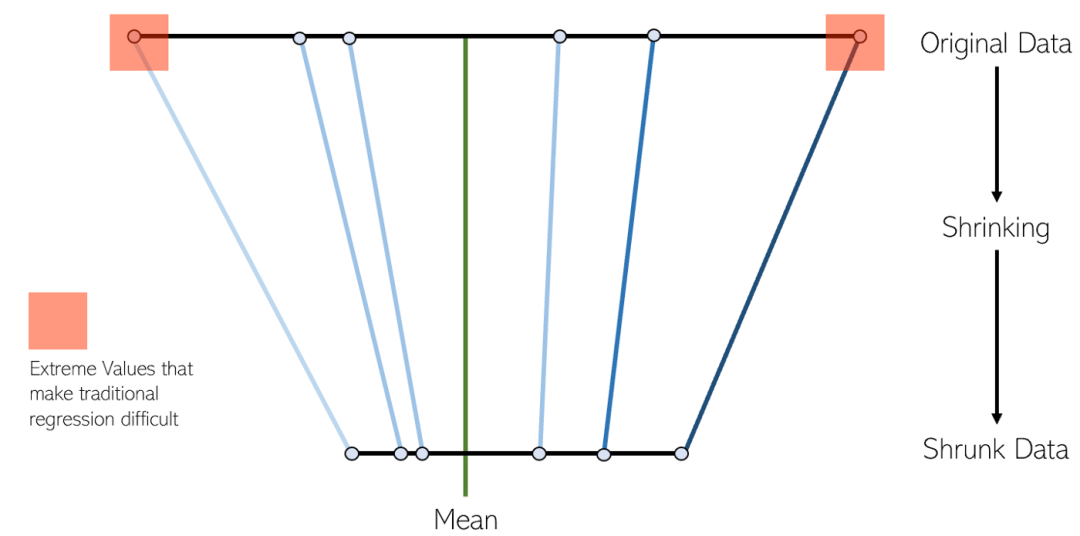
6. Régression LASSO
La régression LASSO est une variante de la régression linéaire par retrait. La réduction est le processus de réduction des valeurs de données jusqu'à un point central en tant que moyenne. Ce type de régression est idéal pour les modèles présentant une multicolinéarité sévère (forte corrélation entre les caractéristiques)

Quelques points sur la régression Lasso :
- Elle est le plus souvent utilisée pour éliminer les variables automatiques et sélectionner les caractéristiques. .
- Il est idéal pour les modèles qui présentent une multicolinéarité sévère (les caractéristiques sont fortement corrélées les unes aux autres).
- La régression LASSO utilise la régularisation L1
- La régression LASSO est considérée comme meilleure que Ridge car elle ne sélectionne que certaines caractéristiques et réduit les coefficients des autres caractéristiques à zéro.
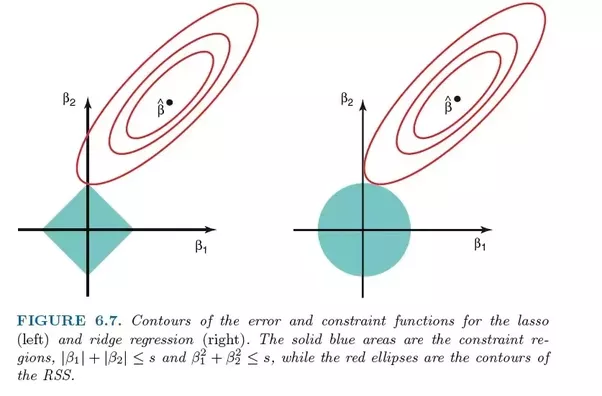
7. Régression Ridge
La régression Ridge est très similaire à la régression LASSO car les deux techniques utilisent des méthodes de retrait. Les régressions Ridge et LASSO conviennent toutes deux aux modèles présentant de graves problèmes de multicolinéarité (c'est-à-dire une corrélation élevée entre les caractéristiques). La principale différence entre eux est que Ridge utilise la régularisation L2, ce qui signifie qu'aucun des coefficients n'ira à zéro (mais proche de zéro) comme dans la régression LASSO

Quelques points sur la régression Ridge :
- Il est idéal pour les modèles qui présentent une multicolinéarité sévère (les caractéristiques sont fortement corrélées les unes aux autres).
- La régression Ridge utilise la régularisation L2. Les fonctionnalités qui contribuent moins auront des coefficients proches de zéro.
- La régression Ridge est considérée comme pire que LASSO en raison de la nature de la régularisation L2.
8. Régression ElasticNet
ElasticNet est un autre modèle de régression linéaire entraîné à l'aide de la régularisation L1 et L2. Il s'agit d'un hybride des techniques de régression Lasso et Ridge, il convient donc également aux modèles présentant une multicolinéarité sévère (les caractéristiques sont fortement corrélées les unes aux autres).
Lors de la pesée entre Lasso et Ridge, un avantage pratique est qu'Elastic-Net peut hériter d'une partie de la stabilité de Ridge sous rotation
9 XGBoost Regression
XGBoost est une version efficace de l'algorithme d'amplification de gradient et. effectivement mis en œuvre. Le boosting de gradient est un type d'algorithme d'apprentissage automatique d'ensemble qui peut être utilisé pour des problèmes de classification ou de régression.
XGBoost est une bibliothèque open source développée à l'origine par Chen Tianqi dans son article de 2016 « XGBoost : A Scalable Tree Boosting System ». L'algorithme est conçu pour être efficace et efficient en termes de calcul
Quelques points sur XGBoost :
- XGBoost ne fonctionne pas bien sur des données clairsemées et non structurées.
- L'algorithme est conçu pour être efficace et efficient sur le plan informatique, mais le temps de formation est encore assez long pour les grands ensembles de données.
- Il est sensible aux valeurs aberrantes.
10. Régression linéaire pondérée locale
Dans la régression linéaire des poids locaux (régression linéaire des poids locaux), nous effectuons également une régression linéaire. Cependant, contrairement à la régression linéaire ordinaire, la régression linéaire pondérée localement est une méthode de régression linéaire locale. En introduisant des poids (fonctions de noyau), lors des prédictions, seuls certains échantillons proches des points de test sont utilisés pour calculer les coefficients de régression. La régression linéaire ordinaire est une régression linéaire globale, qui utilise tous les échantillons pour calculer les coefficients de régression
Avantages et inconvénients et scénarios applicables
L'avantage est d'éviter le sous-ajustement grâce à la pondération des fonctions du noyau, et les inconvénients sont également évidentsK Débogage est requis. Lorsque la régression linéaire multiple est surajustée, vous pouvez essayer la pondération locale du noyau gaussien pour éviter le surajustement.
11. Régression bayésienne de crête
Le modèle de régression linéaire résolu à l'aide de la méthode d'inférence bayésienne est appelé régression linéaire bayésienne
La régression linéaire bayésienne est une méthode qui combine les paramètres d'un modèle linéaire Traiter comme une variable aléatoire et calculer le postérieur à partir du antérieur. La régression linéaire bayésienne peut être résolue par des méthodes numériques et, sous certaines conditions, des statistiques postérieures ou associées sous forme analytique peuvent également être obtenues
La régression linéaire bayésienne a les propriétés de base des modèles statistiques bayésiens et peut résoudre des coefficients de poids Fonction de densité de probabilité , apprentissage en ligne et tests d'hypothèses de modèles basés sur le facteur Bayes (facteur Bayes)
Avantages et inconvénients et scénarios applicables
L'avantage de la régression bayésienne est son adaptabilité des données, peut réutiliser les données et empêcher le surajustement. Dans le processus d'estimation, des termes de régularisation peuvent être introduits.Par exemple, en introduisant le terme de régularisation L2 dans la régression linéaire bayésienne, la régression bayésienne de crête peut être réalisée.L'inconvénient est que le processus d'apprentissage est trop coûteux. Lorsque le nombre de fonctionnalités est inférieur à 10, vous pouvez essayer la régression bayésienne.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Qu'est-ce que l'intelligence artificielle, l'apprentissage automatique et l'apprentissage profond ?
- Introduction aux bibliothèques d'apprentissage automatique et d'apprentissage profond couramment utilisées en python (partage de résumé)
- Intelligence artificielle (IA), apprentissage automatique (ML) et apprentissage profond (DL) : quelle est la différence ?
- Quelles sont les applications du machine learning ?
- Démonstration de la règle 68-95-99.7 dans les statistiques à l'aide de Python

