Maison >Périphériques technologiques >IA >Explorer l'histoire et la matrice de l'intelligence artificielle : tutoriel sur l'intelligence artificielle (2)
Explorer l'histoire et la matrice de l'intelligence artificielle : tutoriel sur l'intelligence artificielle (2)
- PHPzavant
- 2023-11-20 17:25:411852parcourir

Dans le premier article de cette série, nous avons discuté des liens et des différences entre l'intelligence artificielle, l'apprentissage automatique, l'apprentissage profond, la science des données et d'autres domaines. Nous avons également fait des choix difficiles concernant les langages de programmation, les outils et bien plus encore que toute la série utiliserait. Enfin, nous avons également introduit un peu de connaissances matricielles. Dans cet article, nous aborderons en profondeur la matrice, le cœur de l’intelligence artificielle. Mais avant cela, comprenons d’abord l’histoire de l’intelligence artificielle
Pourquoi avons-nous besoin de comprendre l’histoire de l’intelligence artificielle ? Il y a eu de nombreux booms de l’IA au cours de l’histoire, mais dans de nombreux cas, les énormes attentes quant au potentiel de l’IA ne se sont pas concrétisées. Comprendre l’histoire de l’intelligence artificielle peut nous aider à voir si cette vague d’intelligence artificielle créera des miracles ou n’est qu’une autre bulle sur le point d’éclater.
Quand avons-nous commencé à comprendre l’origine de l’intelligence artificielle ? Était-ce après l’invention de l’ordinateur numérique ? Ou plus tôt ? Je crois que la quête d'un être omniscient remonte au début de la civilisation. Par exemple, Delphes dans la mythologie grecque antique était un prophète capable de répondre à n’importe quelle question. La recherche de machines créatives dépassant l’intelligence humaine nous fascine également depuis l’Antiquité. Il y a eu plusieurs tentatives infructueuses de construction de machines d’échecs au cours de l’histoire. Parmi eux se trouve le tristement célèbre Mechanical Turk, qui n'est pas un vrai robot mais est contrôlé par un joueur d'échecs caché à l'intérieur. L'invention des logarithmes de John Napier, la calculatrice de Blaise Pascal et le moteur analytique de Charles Babbage ont tous joué un rôle clé dans le développement de l'intelligence artificielle
Alors, quelles sont les étapes marquantes du développement de l'intelligence artificielle jusqu'à présent ? Comme mentionné précédemment, l’invention de l’ordinateur numérique constitue l’événement le plus important de l’histoire de la recherche sur l’intelligence artificielle. Contrairement aux appareils électromécaniques, dont l'évolutivité dépend des besoins en énergie, les appareils numériques bénéficient des avancées technologiques, comme les tubes à vide, les transistors, les circuits intégrés et maintenant le VLSI.
Une autre étape importante dans le développement de l’intelligence artificielle est la première analyse théorique d’Alan Turing sur l’intelligence artificielle. Il a proposé le célèbre test de Turing
À la fin des années 1950, John McCarthy
Dans les années 1970 et 1980, les algorithmes ont joué un rôle majeur dans cette période. Durant cette période, de nombreux nouveaux algorithmes efficaces ont été proposés. A la fin des années 1960, Donald Knuth (je vous recommande fortement de le connaître, dans le monde informatique, il est l'équivalent de Gauss ou d'Euler dans le monde mathématique) célèbre "L'Art de la programmation informatique". La publication du premier volume de programmation a marqué le début de l’ère des algorithmes. Au cours de ces années, de nombreux algorithmes à usage général et algorithmes graphiques ont été développés. De plus, une programmation basée sur des réseaux de neurones artificiels fait également son apparition à cette époque. Bien que dès les années 1940, Warren S. McCulloch et Walter Pitts
il existe au moins deux opportunités prometteuses pour l'intelligence artificielle à l'ère numérique, mais ces deux opportunités n'ont ni répondu aux attentes. La vague actuelle d’intelligence artificielle est-elle similaire à celle-ci ? Il est difficile de répondre à cette question. Cependant, je crois personnellement que l'intelligence artificielle aura un impact énorme cette fois-ci (annotation de traduction LCTT : cet article a été publié en juin 2022, ChatGTP a été lancé six mois plus tard). Pourquoi ai-je une telle prédiction ? Premièrement, les équipements informatiques hautes performances sont désormais bon marché et facilement disponibles. Dans les années 1960 ou 1980, il n’existait que quelques appareils informatiques aussi puissants, alors qu’aujourd’hui nous en avons des millions, voire des milliards. Deuxièmement, il existe désormais une grande quantité de données disponibles pour la formation de programmes d’intelligence artificielle et d’apprentissage automatique. Imaginez combien d’ingénieurs en images numériques engagés dans le traitement d’images numériques dans les années 1990 pourraient utiliser pour former des algorithmes ? Peut-être des milliers ou des dizaines de milliers. Désormais, la plateforme de science des données Kaggle (filiale de Google) compte à elle seule plus de 10 000 ensembles de données. La grande quantité de données générées quotidiennement par Internet facilite la formation des algorithmes. Troisièmement, les connexions Internet à haut débit facilitent la collaboration avec les grandes institutions. Dans la première décennie du XXIe siècle, la collaboration entre informaticiens était difficile. Cependant, la vitesse d’Internet fait désormais de la collaboration avec des projets d’intelligence artificielle tels que Google Colab, Kaggle et Project Jupiter une réalité. Sur la base de ces trois facteurs, je crois que l'intelligence artificielle existera pour toujours cette fois, et qu'il y aura de nombreuses excellentes applications
Plus de connaissances sur les matrices
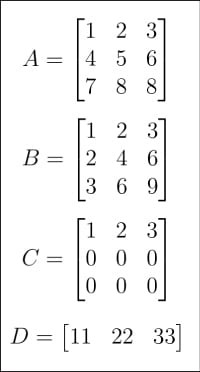 Figure 1 : Matrice A, B, C, D
Figure 1 : Matrice A, B, C, D
Après avoir compris l'histoire de l'intelligence artificielle, il est temps de revenir au sujet des matrices et des vecteurs. Je les ai brièvement présentés dans des articles précédents. Cette fois, nous plongerons plus profondément dans le monde de Matrix. Tout d’abord, regardez les figures 1 et 2, qui montrent un total de 8 matrices de A à H. Pourquoi tant de matrices sont-elles nécessaires dans les didacticiels sur l’intelligence artificielle et l’apprentissage automatique ? Tout d'abord, comme mentionné précédemment, les matrices sont au cœur de l'algèbre linéaire, et l'algèbre linéaire n'est pas le cerveau de l'apprentissage automatique, mais elle est le cœur de l'apprentissage automatique. Deuxièmement, dans la discussion suivante, chaque matrice a un objectif spécifique
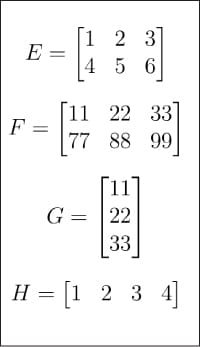 Figure 2 : Matrices E, F, G, H
Figure 2 : Matrices E, F, G, H
Voyons comment les matrices sont représentées et comment obtenir leurs détails. La figure 3 montre comment représenter la matrice A à l'aide de NumPy. Bien que les matrices et les tableaux ne soient pas exactement les mêmes, nous les utilisons souvent comme synonymes dans des applications pratiques
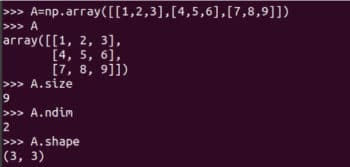 Figure 3 : Représentation de la matrice A dans NumPy
Figure 3 : Représentation de la matrice A dans NumPy
Je vous recommande fortement d'apprendre attentivement à utiliser le array La fonction crée une matrice. Bien que NumPy fournisse également fonction matricielle pour créer des tableaux et des matrices bidimensionnels. Mais il sera obsolète à l’avenir, son utilisation n’est donc plus recommandée. Certains détails de la matrice A sont également présentés sur la figure 3 . A.size nous indique le nombre d'éléments dans le tableau. Dans notre cas, il est 9 heures. Code A.nidm représente la dimension du tableau. Il est facile de voir que la matrice A est bidimensionnelle. A.shape représente l'ordre de la matrice A. L'ordre de la matrice est le nombre de lignes et de colonnes de la matrice. Bien que je ne l'explique pas davantage, vous devez être conscient de la taille, de la dimension et de l'ordre de vos matrices lorsque vous utilisez la bibliothèque NumPy. La figure 4 montre pourquoi la taille, la dimension et l'ordre d'une matrice doivent être soigneusement identifiés. De petites différences dans la façon dont un tableau est défini peuvent entraîner des différences dans sa taille, sa dimensionnalité et son ordre. Par conséquent, les programmeurs doivent accorder une attention particulière à ces détails lors de la définition des matrices. array 函数创建矩阵。虽然 NumPy 也提供了 matrix 函数来创建二维数组和矩阵。但是它将在未来被废弃,所以不再建议使用了。在图 3 还显示了矩阵 A 的一些详细信息。A.size 告诉我们数组中元素的个数。在我们的例子中,它是 9。代码 A.nidm 表示数组的 维数dimension。很容易看出矩阵 A 是二维的。A.shape 表示矩阵 A 的阶数order,矩阵的阶数是矩阵的行数和列数。虽然我不会进一步解释,但使用 NumPy 库时需要注意矩阵的大小、维度和阶数。图 4 显示了为什么应该仔细识别矩阵的大小、维数和阶数。定义数组时的微小差异可能导致其大小、维数和阶数的不同。因此,程序员在定义矩阵时应该格外注意这些细节。
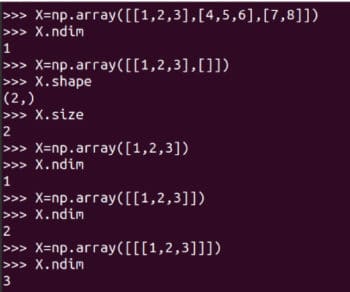 图 4:数组的大小、维数和阶数
图 4:数组的大小、维数和阶数
现在我们来做一些基本的矩阵运算。图 5 显示了如何将矩阵 A 和 B 相加。NumPy 提供了两种方法将矩阵相加,add 函数和 +

Figure 4 : Taille, dimension et ordre du tableau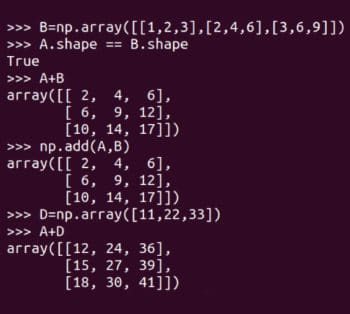 Faisons maintenant quelques opérations matricielles de base. La figure 5 montre comment les matrices A et B sont ajoutées. NumPy fournit deux méthodes pour ajouter des matrices,
Faisons maintenant quelques opérations matricielles de base. La figure 5 montre comment les matrices A et B sont ajoutées. NumPy fournit deux méthodes pour ajouter des matrices, ajouter fonction et +. Notez que seules des matrices du même ordre peuvent être ajoutées. Par exemple, deux matrices 4 × 3 peuvent être ajoutées, mais une matrice 3 × 4 et une matrice 2 × 3 ne peuvent pas être ajoutées. Cependant, comme la programmation est différente des mathématiques, NumPy ne suit pas réellement cette règle. La figure 5 montre également l'ajout des matrices A et D. N'oubliez pas que ce type d'addition matricielle est mathématiquement illégal. L'une s'appelle la diffusion
Réexpression : Figure 5 : Sommation matricielle
🎜🎜Réexpression : Figure 5 : Sommation matricielle🎜A.shape == B.shape🎜Le mécanisme de diffusion n'est pas tout-puissant, si vous essayez d'ajouter les matrices D et H , une erreur de fonctionnement se produira. 🎜
当然除了矩阵加法外还有其它矩阵运算。图 6 展示了矩阵减法和矩阵乘法。它们同样有两种形式,矩阵减法可以由 subtract 函数或减法运算符 - 来实现,矩阵乘法可以由 matmul 函数或矩阵乘法运算符 @ 来实现。图 6 还展示了 逐元素乘法element-wise multiplication 运算符 * 的使用。请注意,只有 NumPy 的 matmul 函数和 @ 运算符执行的是数学意义上的矩阵乘法。在处理矩阵时要小心使用 * 运算符。
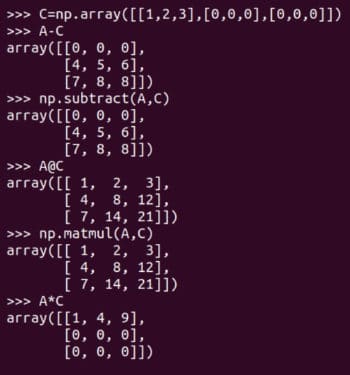 图 6:更多矩阵运算
图 6:更多矩阵运算
对于一个 m x n 阶和一个 p x q 阶的矩阵,当且仅当 n 等于 p 时它们才可以相乘,相乘的结果是一个 m x q 阶矩的阵。图 7 显示了更多矩阵相乘的示例。注意 E@A 是可行的,而 A@E 会导致错误。请仔细阅读对比 D@G 和 G@D 的示例。使用 shape 属性,确定这 8 个矩阵中哪些可以相乘。虽然根据严格的数学定义,矩阵是二维的,但我们将要处理更高维的数组。作为例子,下面的代码创建一个名为 T 的三维数组。
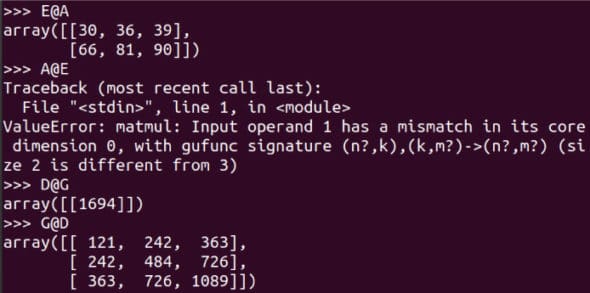 图 7:更多矩阵乘法的例子
图 7:更多矩阵乘法的例子
T = np.array([[[11,22], [33,44]], [[55,66], [77,88]]])
Pandas
到目前为止,我们都是通过键盘输入矩阵的。如果我们需要从文件或数据集中读取大型矩阵并处理,那该怎么办呢?这时我们就要用到另一个强大的 Python 库了——Pandas。我们以读取一个小的 CSV (逗号分隔值comma-separated value)文件为例。图 8 展示了如何读取 cricket.csv 文件,并将其中的前三行打印到终端上。在本系列的后续文章中将会介绍 Pandas 的更多特性。
 图 8:用 Pandas 读取 CSV 文件
图 8:用 Pandas 读取 CSV 文件
图 8:用 Pandas 读取 CSV 文件
矩阵的秩
需要进行改写的内容是:矩阵的秩
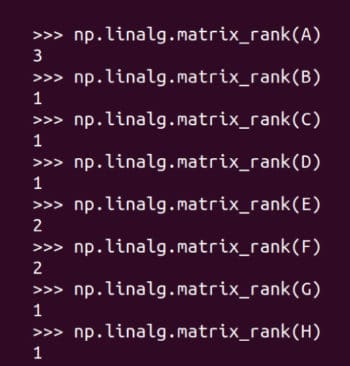 Figure 9 : Trouver le rang de la matrice
Figure 9 : Trouver le rang de la matrice
C'est la fin de ce contenu. Dans le prochain article, nous élargirons la bibliothèque d’outils afin qu’ils puissent être utilisés pour développer des programmes d’intelligence artificielle et d’apprentissage automatique. Nous discuterons également plus en détail du réseau neuronal, de l'apprentissage supervisé et de l'apprentissage non supervisé
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

