Qu’est-ce que la régularisation dans l’apprentissage automatique ?

1. Introduction

Dans le domaine de l'apprentissage automatique, les modèles pertinents peuvent devenir surajustés ou sous-ajustés au cours du processus de formation. Pour éviter que cela ne se produise, nous utilisons des opérations de régularisation dans l'apprentissage automatique pour ajuster correctement le modèle sur notre ensemble de test. De manière générale, les opérations de régularisation aident chacun à obtenir le meilleur modèle en réduisant les risques de surajustement et de sous-ajustement.

Dans cet article, nous comprendrons ce qu'est la régularisation, les types de régularisation. De plus, nous discuterons de concepts connexes tels que le biais, la variance, le sous-apprentissage et le surapprentissage.

Fini les bêtises, c'est parti !

2. Biais et variance

Le biais et la variance sont deux aspects utilisés pour décrire l'écart entre le modèle que nous avons appris et le modèle réel

Ce qui doit être réécrit, c'est : les deux C'est défini comme suit :

• Le biais est la différence entre la moyenne de la sortie de tous les modèles entraînés avec tous les ensembles de données d'entraînement possibles et la valeur de sortie du modèle réel.
• La variance est la différence entre les valeurs de sortie du modèle entraîné sur différents ensembles de données d'entraînement.

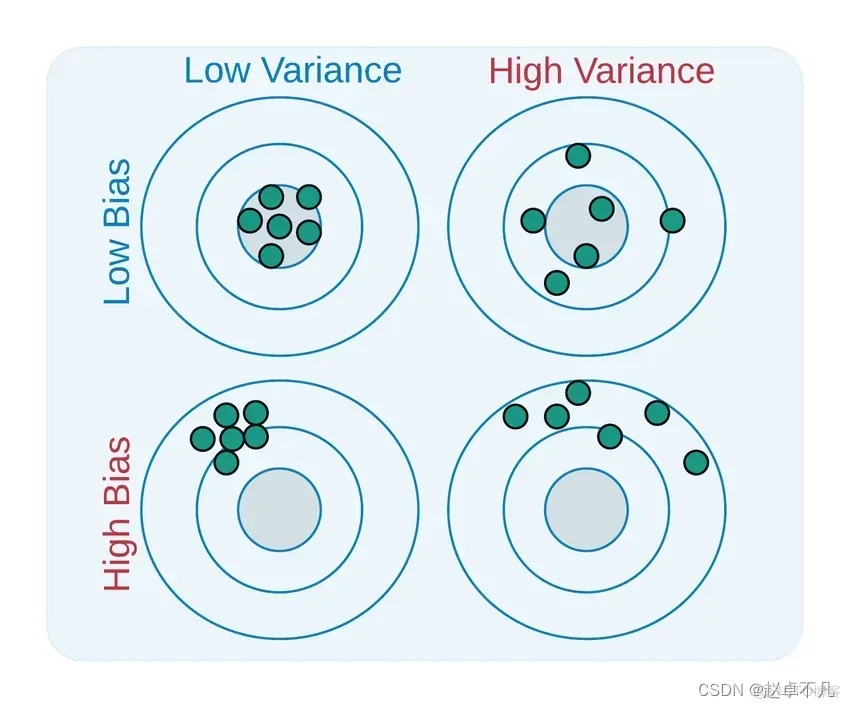
Le biais réduit la sensibilité du modèle aux points de données individuels, tout en augmentant la généralisation des données et en réduisant la sensibilité du modèle aux points de données isolés. Le temps de formation peut également être réduit puisque la fonctionnalité requise est moins complexe. Un biais élevé indique que la fonction cible est supposée plus fiable, mais peut parfois conduire à un sous-ajustement du modèle

La variance (Variance) dans l'apprentissage automatique fait référence aux erreurs causées par la sensibilité du modèle à de petits changements dans les données ensemble. Puisqu’il existe une variation significative dans l’ensemble de données, l’algorithme modélise le bruit et les valeurs aberrantes dans l’ensemble d’apprentissage. Cette situation est souvent appelée surapprentissage. Lorsqu'il est évalué sur un nouvel ensemble de données, il ne peut pas fournir de prédictions précises car le modèle apprend essentiellement chaque point de données

Un modèle relativement équilibré aura un faible biais et une faible variance, tandis qu'un biais élevé et une variance élevée conduiront à sous-apprentissage et surapprentissage.

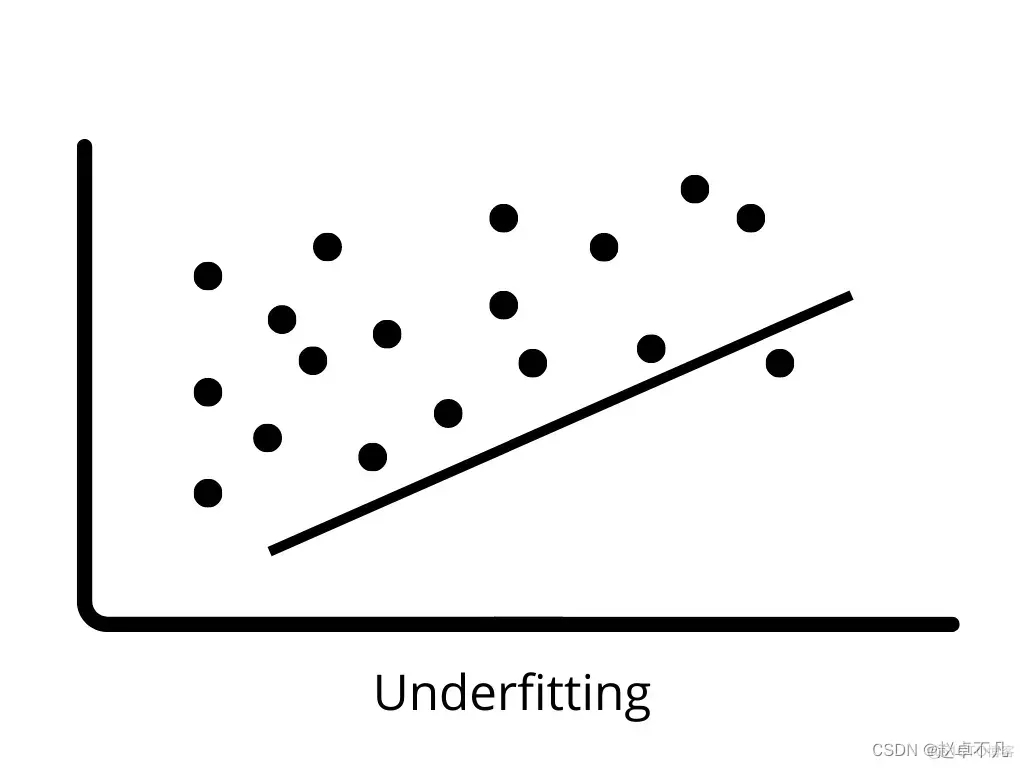
3. Sous-ajustement

Un sous-ajustement se produit lorsque le modèle ne peut pas apprendre correctement les modèles dans les données d'entraînement et les généraliser à de nouvelles données. Les modèles de sous-ajustement fonctionnent mal sur les données d'entraînement et peuvent conduire à des prédictions incorrectes. Lorsqu'un biais élevé et une faible variance se produisent, un sous-ajustement est susceptible de se produire

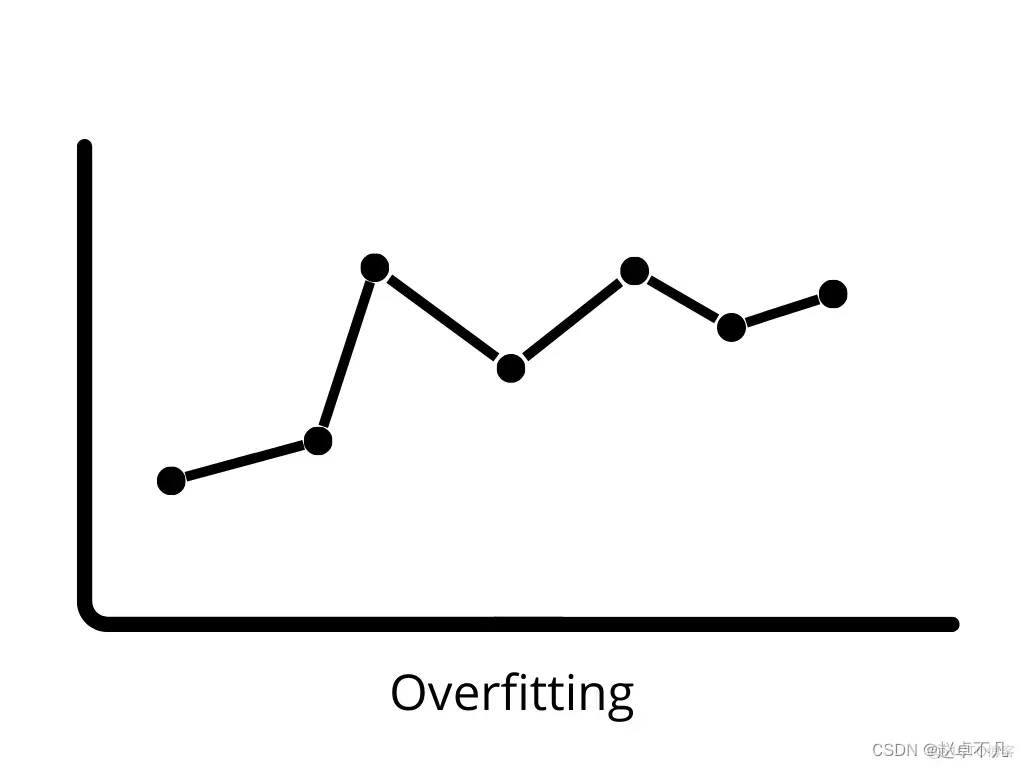
4. Surajustement

Lorsqu'un modèle fonctionne très bien sur les données d'entraînement, mais échoue sur les données de test. mal sur les nouvelles données, on parle de surapprentissage. Dans ce cas, le modèle d'apprentissage automatique est adapté au bruit présent dans les données d'entraînement, ce qui affecte négativement les performances du modèle sur les données de test. Un biais faible et une variance élevée peuvent conduire à un surapprentissage.

5. Concept de régularisation

Le terme « régularisation » décrit la méthode de calibrage d'un modèle d'apprentissage automatique pour réduire la fonction de perte ajustée et éviter le surajustement ou le sous-ajustement.

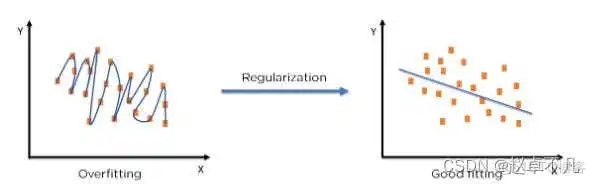
En utilisant la technologie de régularisation, nous pouvons adapter le modèle d'apprentissage automatique avec plus de précision à un ensemble de tests spécifique, réduisant ainsi efficacement l'erreur dans l'ensemble de tests

6. Régularisation L1

Par rapport à la régression du collier, la mise en œuvre de la régularisation L1 consiste principalement à ajouter un terme de pénalité à la fonction de perte. La valeur de pénalité de ce terme est la somme des valeurs absolues de tous les coefficients, comme suit :

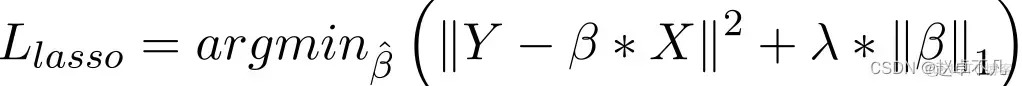
Dans le modèle de régression Lasso, ceci est obtenu en augmentant le terme de pénalité de la valeur absolue du coefficient de régression d'une manière similaire à la régression de crête. De plus, la régularisation L1 a de bonnes performances pour améliorer la précision des modèles de régression linéaire. Dans le même temps, puisque la régularisation L1 pénalise tous les paramètres de manière égale, elle peut rendre certains poids nuls, produisant ainsi un modèle clairsemé qui peut supprimer certaines caractéristiques (un poids de 0 équivaut à une suppression).

7. La régularisation L2

La régularisation L2 est également obtenue en ajoutant un terme de pénalité à la fonction de perte, qui est égal à la somme des carrés de tous les coefficients. Comme indiqué ci-dessous :

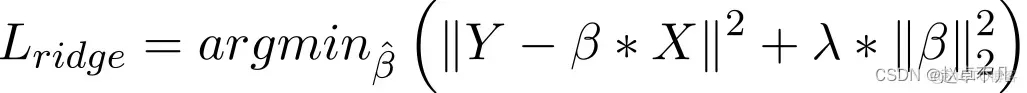
De manière générale, elle est considérée comme une méthode à adopter lorsque les données présentent une multicolinéarité (les variables indépendantes sont fortement corrélées). Bien que les estimations des moindres carrés (OLS) en multicolinéarité soient impartiales, leurs écarts importants peuvent entraîner une différence significative entre les valeurs observées et les valeurs réelles. L2 réduit dans une certaine mesure l’erreur des estimations de régression. Il utilise généralement des paramètres de retrait pour résoudre des problèmes de multicolinéarité. La régularisation L2 réduit la proportion fixe de poids et lisse les poids.

8. Résumé

Après l'analyse ci-dessus, les connaissances pertinentes en matière de régularisation dans cet article sont résumées comme suit :

La régularisation L1 peut générer une matrice de poids clairsemée, c'est-à-dire générer un modèle clairsemé. , qui peut Utilisé pour la sélection des fonctionnalités ;

La régularisation L2 peut empêcher le surajustement du modèle. Dans une certaine mesure, L1 peut également empêcher le surajustement et améliorer la capacité de généralisation du modèle

Paramètres de l'hypothèse de régularisation L1 (lagrangienne). La distribution de Laplace, qui peut garantir la parcimonie du modèle, c'est-à-dire que certains paramètres sont égaux à 0 ; l'hypothèse de

L2 (régression de crête) est que la distribution a priori des paramètres est une distribution gaussienne, ce qui peut assurer la stabilité du modèle, c'est-à-dire que la valeur du paramètre ne sera ni trop grande ni trop petite

Dans les applications pratiques, si la caractéristique est de grande dimension et clairsemée, la régularisation L1 doit être utilisée si la caractéristique est de faible dimension et dense ; , la régularisation L2 doit être utilisée

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!