Les articles précédents ont présenté la normalisation des fonctionnalités et les tenseurs. Ensuite, j'écrirai deux tutoriels concis sur PyTorch, présentant principalement des pratiques simples de PyTorch.
1 Figure 1import torcha = torch.tensor([2, 3, 4])b = torch.tensor([3, 4, 5])print("a + b: ", (a + b).numpy())print("a - b: ", (a - b).numpy())print("a * b: ", (a * b).numpy())print("a / b: ", (a / b).numpy())
(1) Commencez par la fonction principale torch.manual_seed(42) est utilisé pour définir la graine du générateur de nombres aléatoires afin de garantir que la séquence de nombres aléatoires générée est la même à chaque fois. run. Cette fonction accepte un nombre entier. Les paramètres servent de graines et peuvent être utilisés dans des scénarios qui nécessitent des nombres aléatoires tels que la formation de réseaux de neurones pour garantir la répétabilité des résultats
(2) torch.linspace(-1, 1, 101, require_grad ; =False) est utilisé pour spécifier Générer un ensemble de valeurs équidistantes dans l'intervalle. Cette fonction accepte trois paramètres : valeur de départ, valeur de fin et nombre d'éléments, et renvoie un tenseur contenant le nombre spécifié de valeurs équidistantes ;
(3) Implémentation interne de build_model1 :torch.nn.Sequential(torch.nn.Linear(1, 1, biais=False)) utilise le constructeur de la classe nn.Sequential, lui passe la couche linéaire comme un paramètre et renvoie Un modèle de réseau neuronal contenant la couche linéaire ;  build_model2 a la même fonction que build_model1, en utilisant la méthode add_module() pour y ajouter un sous-module nommé Linear ; (reductinotallow='mean') définit la fonction de perte ;
build_model2 a la même fonction que build_model1, en utilisant la méthode add_module() pour y ajouter un sous-module nommé Linear ; (reductinotallow='mean') définit la fonction de perte ;
- model : modèle de réseau neuronal, généralement. un hérité de l'instance de la classe nn.Module ;
- loss : fonction de perte, utilisée pour calculer la différence entre la valeur prédite et la valeur réelle du modèle ;
- optimizer : optimiseur, utilisé pour mettre à jour les paramètres du modèle ;
x : données d'entrée, est un tenseur de type torch.Tensor ;
y : données cibles, est un tenseur de type torch.Tensor
(8) train est une méthode couramment utilisée dans le processus de formation PyTorch, et ses étapes sont les suivantes :- Définissez le modèle en mode entraînement, c'est-à-dire activez les opérations spéciales utilisées pendant l'entraînement telles que l'abandon et la normalisation par lots
- Effacez le cache de gradient de l'optimiseur pour un nouveau cycle de calcul de gradient ;
- Transmettez les données d'entrée au modèle, calculez la valeur prédite du modèle et transmettez la valeur prédite et les données cibles à la fonction de perte pour calculer la valeur de perte
- Rétropropagez la valeur de perte et calculez le gradient des paramètres du modèle ; ;
- Utilisez l'optimiseur pour mettre à jour les paramètres du modèle afin de minimiser Transformer la valeur de perte ;
- Renvoyer la valeur scalaire de la valeur de perte
a + b:[5 7 9]a - b:[-1 -1 -1]a * b:[ 6 12 20]a / b:[0.6666667 0.750.8]
import torchfrom torch import optimdef build_model1():return torch.nn.Sequential(torch.nn.Linear(1, 1, bias=False))def build_model2():model = torch.nn.Sequential()model.add_module("linear", torch.nn.Linear(1, 1, bias=False))return modeldef train(model, loss, optimizer, x, y):model.train()optimizer.zero_grad()fx = model.forward(x.view(len(x), 1)).squeeze()output = loss.forward(fx, y)output.backward()optimizer.step()return output.item()def main():torch.manual_seed(42)X = torch.linspace(-1, 1, 101, requires_grad=False)Y = 2 * X + torch.randn(X.size()) * 0.33print("X: ", X.numpy(), ", Y: ", Y.numpy())model = build_model1()loss = torch.nn.MSELoss(reductinotallow='mean')optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)batch_size = 10for i in range(100):cost = 0.num_batches = len(X) // batch_sizefor k in range(num_batches):start, end = k * batch_size, (k + 1) * batch_sizecost += train(model, loss, optimizer, X[start:end], Y[start:end])print("Epoch = %d, cost = %s" % (i + 1, cost / num_batches))w = next(model.parameters()).dataprint("w = %.2f" % w.numpy())if __name__ == "__main__":main()(3) implémentation interne de build_model : torch.nn.Sequential(torch.nn.Linear(input_dim, output_dim, biais=False)) est utilisé pour construire un modèle de réseau neuronal contenant une couche linéaire, le nombre d'entités d'entrée du modèle est input_dim, le nombre d'entités de sortie est output_dim et la couche linéaire n'a pas de terme de biais, où n_classes=10 signifie produire 10 catégories ; Après réécriture : (3) Implémentation interne de build_model : utilisez torch.nn.Sequential(torch.nn.Linear(input_dim, output_dim,bias=False)) pour créer un modèle de réseau neuronal contenant une couche linéaire. Le nombre de fonctionnalités d'entrée du modèle est. input_dim. Le nombre d'entités en sortie est output_dim et la couche linéaire n'a pas de terme de biais. Parmi eux, n_classes=10 signifie générer 10 catégories ;
(4) Les autres étapes consistent à définir la fonction de perte, l'optimiseur de descente de gradient, à diviser l'ensemble d'entraînement via batch_size et à boucler 100 fois pour l'entraînement
Utilisez optim.SGD ; (model .parameters(), lr=0.01, momentum=0.9) peut implémenter l'algorithme d'optimisation de descente de gradient stochastique (SGD)
(6) Après chaque cycle d'entraînement, la fonction de prévision doit être exécutée pour faire des prédictions. Cette fonction accepte deux paramètres modèle (le modèle entraîné) et teX (les données qui doivent être prédites). Les étapes spécifiques sont les suivantes : 
- model.eval()模型设置为评估模式,这意味着模型将不会进行训练,而是仅用于推理;
- 将output转换为NumPy数组,并使用argmax()方法获取每个样本的预测类别;
(7)print("Epoch %d, cost = %f, acc = %.2f%%" % (i + 1, cost / num_batches, 100. * np.mean(predY == teY)))最后打印当前训练的轮次,损失值和acc,上述的代码输出如下(执行很快,但是准确率偏低):
...Epoch 91, cost = 0.252863, acc = 92.52%Epoch 92, cost = 0.252717, acc = 92.51%Epoch 93, cost = 0.252573, acc = 92.50%Epoch 94, cost = 0.252431, acc = 92.50%Epoch 95, cost = 0.252291, acc = 92.52%Epoch 96, cost = 0.252153, acc = 92.52%Epoch 97, cost = 0.252016, acc = 92.51%Epoch 98, cost = 0.251882, acc = 92.51%Epoch 99, cost = 0.251749, acc = 92.51%Epoch 100, cost = 0.251617, acc = 92.51%
4、神经网络
一个经典的LeNet网络,用于对字符进行分类,如图:
 图3
图3
- 定义一个多层的神经网络
- 对数据集的预处理并准备作为网络的输入
- 将数据输入到网络
- 计算网络的损失
- 反向传播,计算梯度
import numpy as npimport torchfrom torch import optimfrom data_util import load_mnistdef build_model(input_dim, output_dim):return torch.nn.Sequential(torch.nn.Linear(input_dim, 512, bias=False),torch.nn.Sigmoid(),torch.nn.Linear(512, output_dim, bias=False))def train(model, loss, optimizer, x_val, y_val):model.train()optimizer.zero_grad()fx = model.forward(x_val)output = loss.forward(fx, y_val)output.backward()optimizer.step()return output.item()def predict(model, x_val):model.eval()output = model.forward(x_val)return output.data.numpy().argmax(axis=1)def main():torch.manual_seed(42)trX, teX, trY, teY = load_mnist(notallow=False)trX = torch.from_numpy(trX).float()teX = torch.from_numpy(teX).float()trY = torch.tensor(trY)n_examples, n_features = trX.size()n_classes = 10model = build_model(n_features, n_classes)loss = torch.nn.CrossEntropyLoss(reductinotallow='mean')optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)batch_size = 100for i in range(100):cost = 0.num_batches = n_examples // batch_sizefor k in range(num_batches):start, end = k * batch_size, (k + 1) * batch_sizecost += train(model, loss, optimizer,trX[start:end], trY[start:end])predY = predict(model, teX)print("Epoch %d, cost = %f, acc = %.2f%%"% (i + 1, cost / num_batches, 100. * np.mean(predY == teY)))if __name__ == "__main__":main()
(1)以上这段神经网络的代码与逻辑回归没有太多的差异,区别的地方是build_model,这里是构建一个包含两个线性层和一个Sigmoid激活函数的神经网络模型,该模型包含一个输入特征数量为input_dim,输出特征数量为output_dim的线性层,一个Sigmoid激活函数,以及一个输入特征数量为512,输出特征数量为output_dim的线性层;
(2)print("Epoch %d, cost = %f, acc = %.2f%%" % (i + 1, cost / num_batches, 100. * np.mean(predY == teY)))最后打印当前训练的轮次,损失值和acc,上述的代码输入如下(执行时间比逻辑回归要长,但是准确率要高很多):
第91个时期,费用= 0.054484,准确率= 97.58%第92个时期,费用= 0.053753,准确率= 97.56%第93个时期,费用= 0.053036,准确率= 97.60%第94个时期,费用= 0.052332,准确率= 97.61%第95个时期,费用= 0.051641,准确率= 97.63%第96个时期,费用= 0.050964,准确率= 97.66%第97个时期,费用= 0.050298,准确率= 97.66%第98个时期,费用= 0.049645,准确率= 97.67%第99个时期,费用= 0.049003,准确率= 97.67%第100个时期,费用= 0.048373,准确率= 97.68%
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
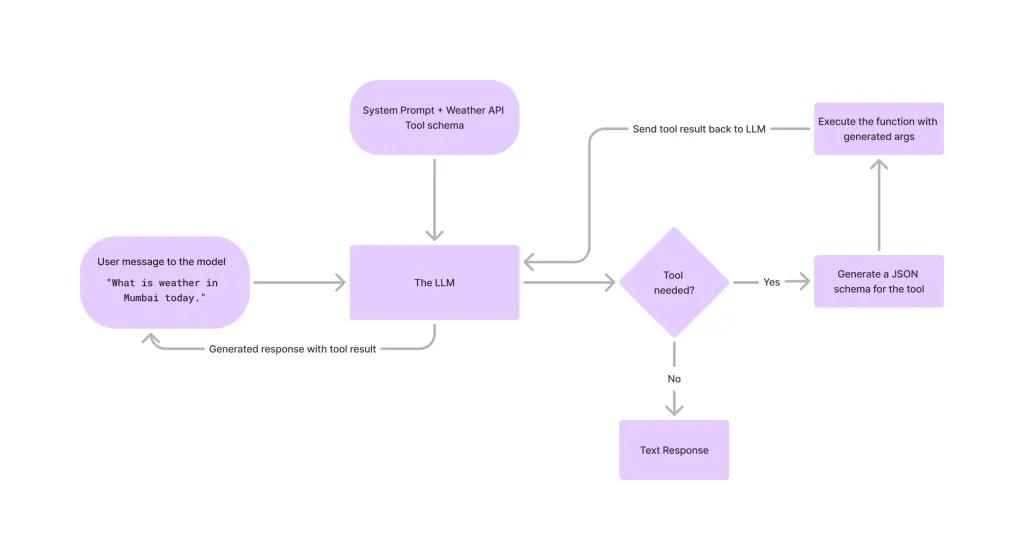 Appel d'outil dans LLMSApr 14, 2025 am 11:28 AM
Appel d'outil dans LLMSApr 14, 2025 am 11:28 AMLes modèles de grands langues (LLM) ont augmenté en popularité, la fonctionnalité d'appel à l'outil élargissant considérablement leurs capacités au-delà de la génération de texte simple. Maintenant, les LLM peuvent gérer des tâches d'automatisation complexes telles que la création d'interface utilisateur dynamique et l'autonomie A
 Comment les jeux de TDAH, les outils de santé et les chatbots d'IA transforment la santé mondialeApr 14, 2025 am 11:27 AM
Comment les jeux de TDAH, les outils de santé et les chatbots d'IA transforment la santé mondialeApr 14, 2025 am 11:27 AMUn jeu vidéo peut-il faciliter l'anxiété, se concentrer ou soutenir un enfant atteint de TDAH? Au fur et à mesure que les défis de la santé augmentent à l'échelle mondiale - en particulier chez les jeunes - les innovateurs se tournent vers un outil improbable: les jeux vidéo. Maintenant l'un des plus grands divertissements du monde Indus
 Entrée des Nations Unies sur l'IA: gagnants, perdants et opportunitésApr 14, 2025 am 11:25 AM
Entrée des Nations Unies sur l'IA: gagnants, perdants et opportunitésApr 14, 2025 am 11:25 AM«L'histoire a montré que bien que les progrès technologiques stimulent la croissance économique, elle n'assure pas elle-même une répartition des revenus équitable ou la promotion du développement humain inclusif», écrit Rebeca Grynspan, secrétaire général de la CNUCTAD, dans le préambule.
 Compétences de négociation d'apprentissage via une IA générativeApr 14, 2025 am 11:23 AM
Compétences de négociation d'apprentissage via une IA générativeApr 14, 2025 am 11:23 AMEasy PEASY, utilisez une IA générative comme tuteur de négociation et partenaire d'entraînement. Parlons-en. Cette analyse d'une percée innovante de l'IA fait partie de ma couverture de colonne Forbes en cours sur la dernière IA, y compris l'identification et l'explication
 Ted révèle d'Openai, Google, Meta se dirige vers le tribunal, Selfie avec moi-mêmeApr 14, 2025 am 11:22 AM
Ted révèle d'Openai, Google, Meta se dirige vers le tribunal, Selfie avec moi-mêmeApr 14, 2025 am 11:22 AMLa conférence TED2025, qui s'est tenue à Vancouver, a terminé sa 36e édition hier 11 avril. Il a présenté 80 conférenciers de plus de 60 pays, dont Sam Altman, Eric Schmidt et Palmer Luckey. Le thème de Ted, «l'humanité repensée», a été fait sur mesure
 Joseph Stiglitz met en garde contre l'inégalité imminente au milieu du pouvoir monopoleApr 14, 2025 am 11:21 AM
Joseph Stiglitz met en garde contre l'inégalité imminente au milieu du pouvoir monopoleApr 14, 2025 am 11:21 AMJoseph Stiglitz est économiste de renom et récipiendaire du prix Nobel en économie en 2001. Stiglitz postule que l'IA peut aggraver les inégalités existantes et le pouvoir consolidé entre les mains de quelques sociétés dominantes, sapant finalement économique économique
 Qu'est-ce que la base de données de graphiques?Apr 14, 2025 am 11:19 AM
Qu'est-ce que la base de données de graphiques?Apr 14, 2025 am 11:19 AMBases de données graphiques: révolutionner la gestion des données à travers les relations À mesure que les données se développent et que ses caractéristiques évoluent sur divers champs, les bases de données de graphiques émergent comme des solutions transformatrices pour gérer les données interconnectées. Contrairement à la traditionnelle
 Routage LLM: stratégies, techniques et implémentation PythonApr 14, 2025 am 11:14 AM
Routage LLM: stratégies, techniques et implémentation PythonApr 14, 2025 am 11:14 AMRoutage de modèle de grande langue (LLM): optimiser les performances grâce à une distribution de tâches intelligente Le paysage en évolution rapide de LLMS présente une gamme diversifiée de modèles, chacun avec des forces et des faiblesses uniques. Certains excellent dans le contenu créatif Gen


Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

SublimeText3 version anglaise
Recommandé : version Win, prend en charge les invites de code !

Navigateur d'examen sécurisé
Safe Exam Browser est un environnement de navigation sécurisé permettant de passer des examens en ligne en toute sécurité. Ce logiciel transforme n'importe quel ordinateur en poste de travail sécurisé. Il contrôle l'accès à n'importe quel utilitaire et empêche les étudiants d'utiliser des ressources non autorisées.

ZendStudio 13.5.1 Mac
Puissant environnement de développement intégré PHP

Dreamweaver Mac
Outils de développement Web visuel

Dreamweaver CS6
Outils de développement Web visuel






