11 visualisations avancées pour l'analyse des données et l'apprentissage automatique

La visualisation est un outil puissant pour communiquer des modèles et des relations de données complexes de manière intuitive et compréhensible. Ils jouent un rôle essentiel dans l’analyse des données, fournissant des informations souvent difficiles à discerner à partir de données brutes ou de représentations numériques traditionnelles.

La visualisation est cruciale pour comprendre les modèles et les relations de données complexes. Nous présenterons les 11 graphiques les plus importants et incontournables qui aident à révéler les informations contenues dans les données et à rendre les données complexes plus compréhensibles et significatives.

1. KS Plot

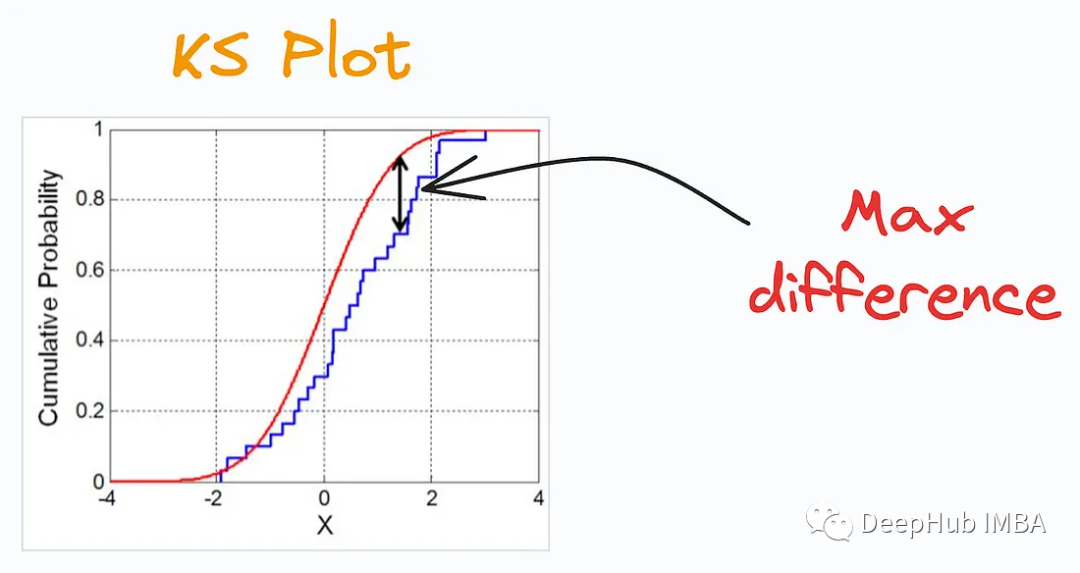
KS Plot est utilisé pour évaluer les différences de distribution. L'idée principale est de mesurer la distance maximale entre les fonctions de distribution cumulatives (CDF) de deux distributions. Plus la distance maximale est petite, plus ils appartiennent probablement à la même distribution. Il est donc principalement interprété comme un « test statistique » pour déterminer la différence de distribution, plutôt que comme un « tracé ».

2. SHAP Plot

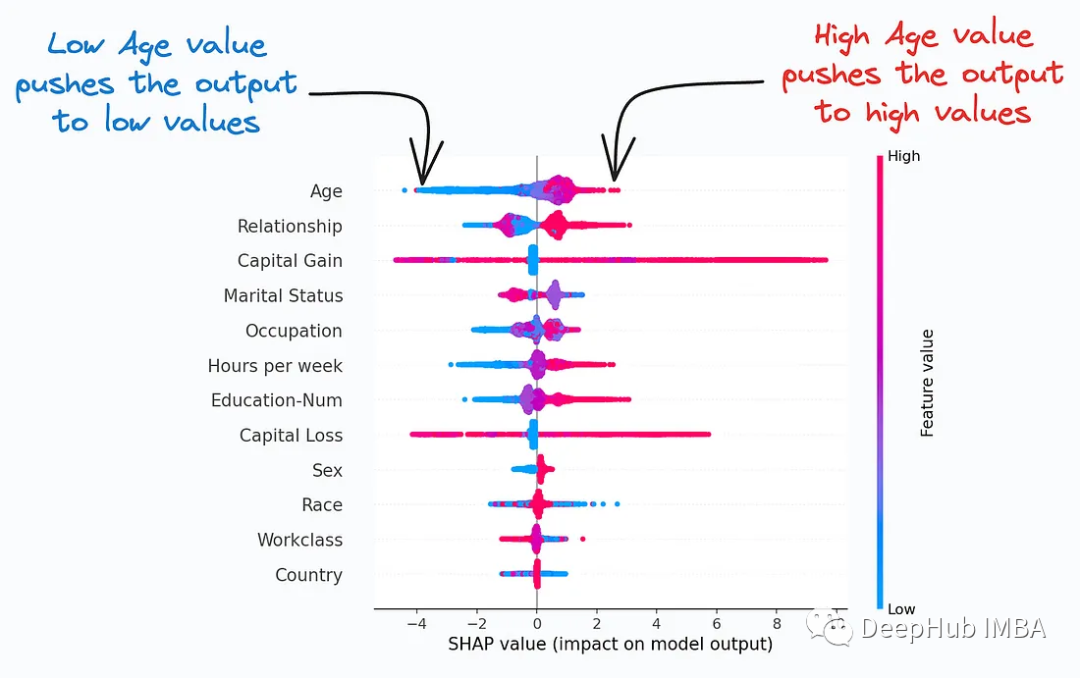
SHAP Plot résume l'importance des fonctionnalités pour la prédiction du modèle en considérant les interactions/dépendances entre les fonctionnalités. Utile pour déterminer comment différentes valeurs (faibles ou élevées) d'une fonctionnalité affectent la sortie globale.

3, Courbe ROC

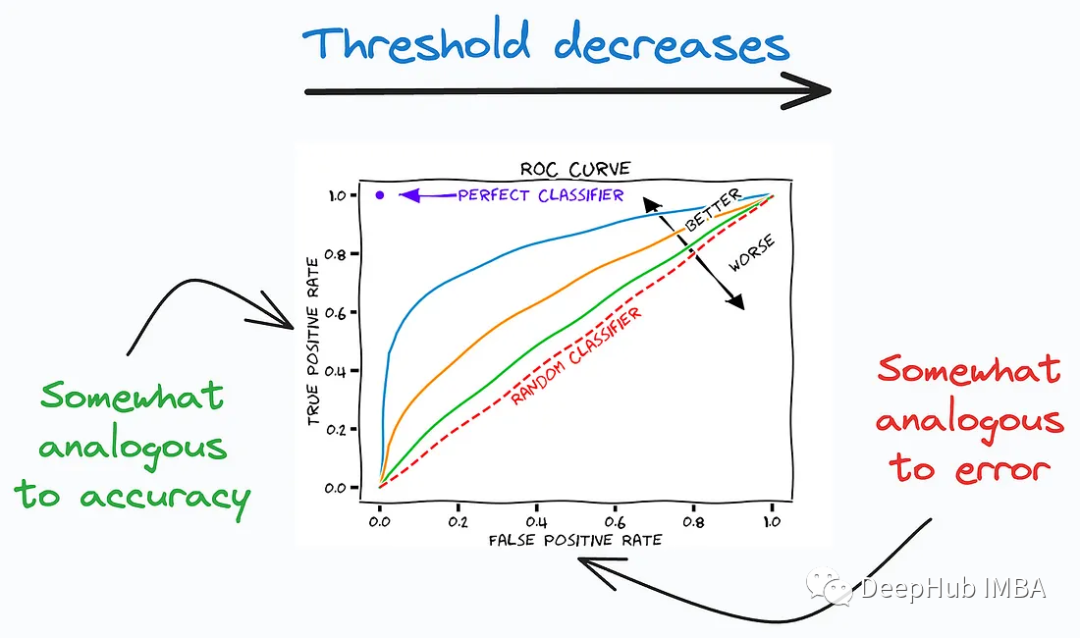
La courbe ROC décrit le compromis entre le taux de vrais positifs (bonnes performances) et le taux de faux positifs (mauvaises performances) à travers différents seuils de classification. Il montre le compromis entre la sensibilité (True Positive Rate, TPR) et la spécificité (True Negative Rate, TNR) du classificateur à différents seuils.

La courbe ROC est un outil couramment utilisé, particulièrement adapté à l'évaluation des performances des tests de diagnostic médical, des classificateurs d'apprentissage automatique, des modèles de risque, etc. En analysant les courbes ROC et en calculant l'AUC, vous pouvez mieux comprendre les performances de votre classificateur, sélectionner les seuils appropriés et comparer les performances entre différents modèles.

4. Courbe de rappel de précision

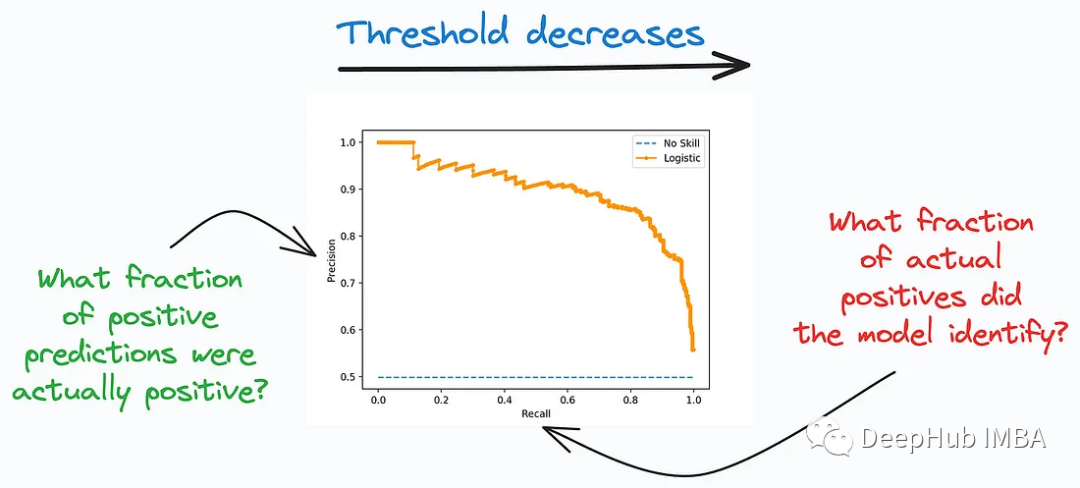
La courbe de rappel de précision (précision-rappel) est un autre outil important pour évaluer les performances des modèles de classification, particulièrement adapté aux distributions de classes déséquilibrées Problème dans lequel le nombre de les échantillons de classe positifs et négatifs sont très différents. Cette courbe se concentre sur la précision des prédictions du modèle dans la catégorie positive et sur sa capacité à trouver tous les vrais exemples positifs. Il décrit le compromis entre précision et rappel entre différents seuils de classification.

5, QQ Plot

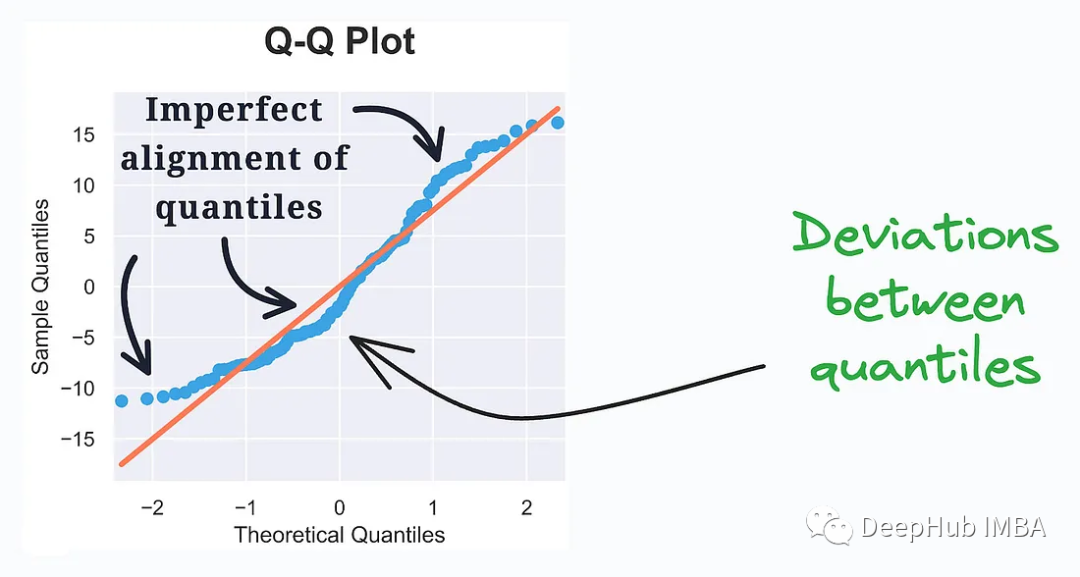
QQ Plot (Quantile-Quantile Plot, quantile-quantile plot) est une méthode utilisée pour comparer si les distributions quantiles de deux ensembles de données sont similaires. Il est souvent utilisé pour vérifier si un ensemble de données est conforme à une distribution théorique spécifique, telle que la distribution normale.

Il évalue la similarité de distribution entre les données observées et la distribution théorique. Les quantiles des deux distributions sont tracés. Un écart par rapport à une ligne droite représente un écart par rapport à la distribution supposée.

QQ Plot est un outil intuitif qui peut être utilisé pour examiner la distribution des données, en particulier dans la modélisation statistique et l'analyse des données. En observant la position des points sur le tracé QQ, vous pouvez comprendre si les données sont conformes à une certaine distribution théorique ou s'il existe des valeurs aberrantes ou des écarts.

6. Le tracé de la variance expliquée cumulative

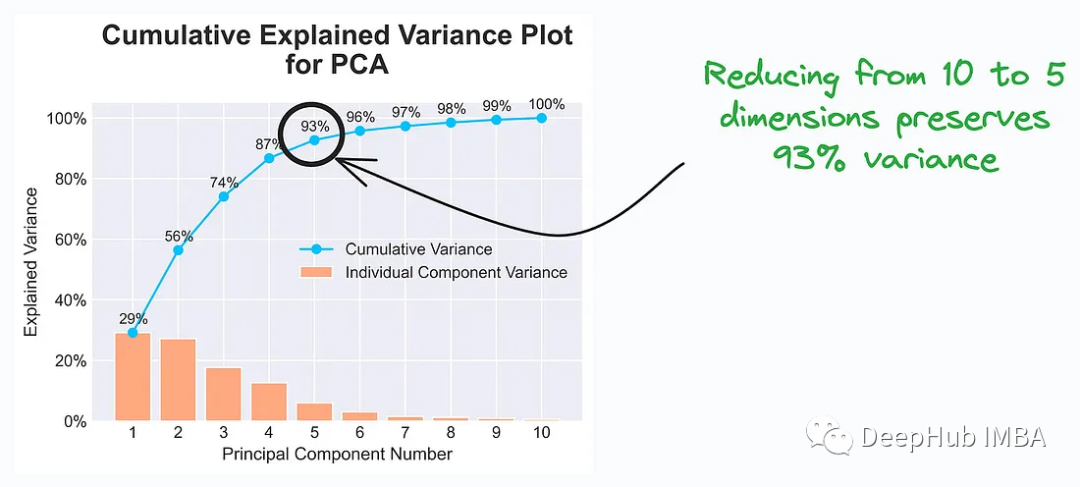
Le tracé de la variance expliquée cumulative (tracé de la variance expliquée cumulative) est un graphique couramment utilisé dans les techniques de réduction de dimensionnalité telles que l'analyse en composantes principales (ACP) pour aider à expliquer les données à inclure. informations sur la variance et choisissez les dimensions appropriées pour représenter les données.

Les data scientists et les analystes choisiront le nombre approprié de composantes principales en fonction des informations contenues dans le diagramme de variance expliquée cumulative afin que les caractéristiques des données puissent toujours être représentées efficacement après la réduction de la dimensionnalité. Cela permet de réduire les dimensions des données, d'améliorer l'efficacité de la formation des modèles et de conserver suffisamment d'informations pour permettre la réussite des tâches.

7. Elbow Curve

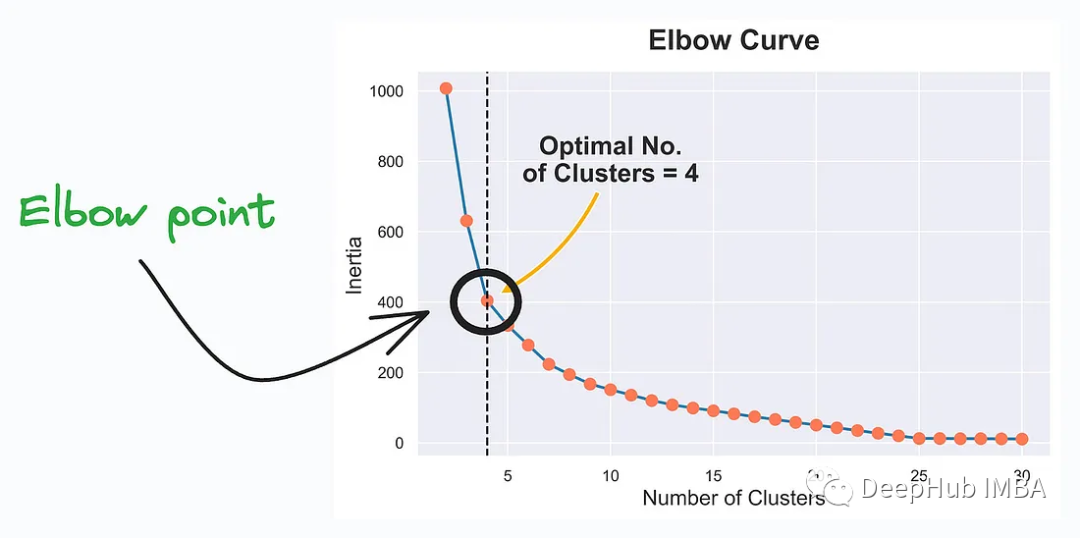
Elbow Curve est un outil de visualisation utilisé pour aider à déterminer le nombre optimal de clusters (nombre de clusters) dans le clustering K-Means. K-Means est un algorithme d'apprentissage non supervisé couramment utilisé pour classer les points de données en différents clusters ou groupes. Elbow Curve aide à trouver le bon nombre de clusters pour représenter au mieux la structure de vos données.

Elbow Curve est un outil couramment utilisé pour aider à sélectionner le nombre optimal de clusters dans le clustering K-Means. Les points au coude représentent le nombre idéal de clusters. Cela capture mieux la structure et les modèles sous-jacents des données.

8, Silhouette Curve

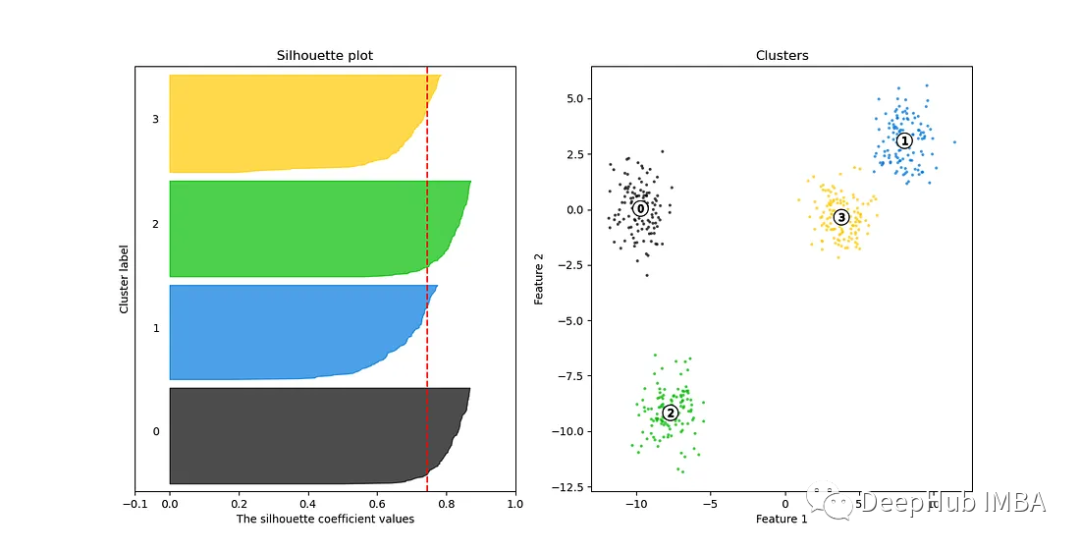
Silhouette Curve (courbe de coefficient de silhouette) est un outil visuel utilisé pour évaluer la qualité du clustering et est souvent utilisé pour aider à sélectionner le nombre optimal de clusters. Le coefficient de silhouette est une mesure de la similarité des points de données au sein des clusters et de la séparation des points de données entre les clusters dans le clustering.

Silhouette Curve est un outil puissant utilisé pour aider à sélectionner le nombre optimal de clusters afin de garantir que le modèle de clustering peut capturer efficacement la structure et les modèles intrinsèques des données. Les courbes coudées sont généralement inefficaces lorsqu’il existe de nombreux clusters. Silhouette Curve est un meilleur choix.

9, Gini-Impurity et Entropy

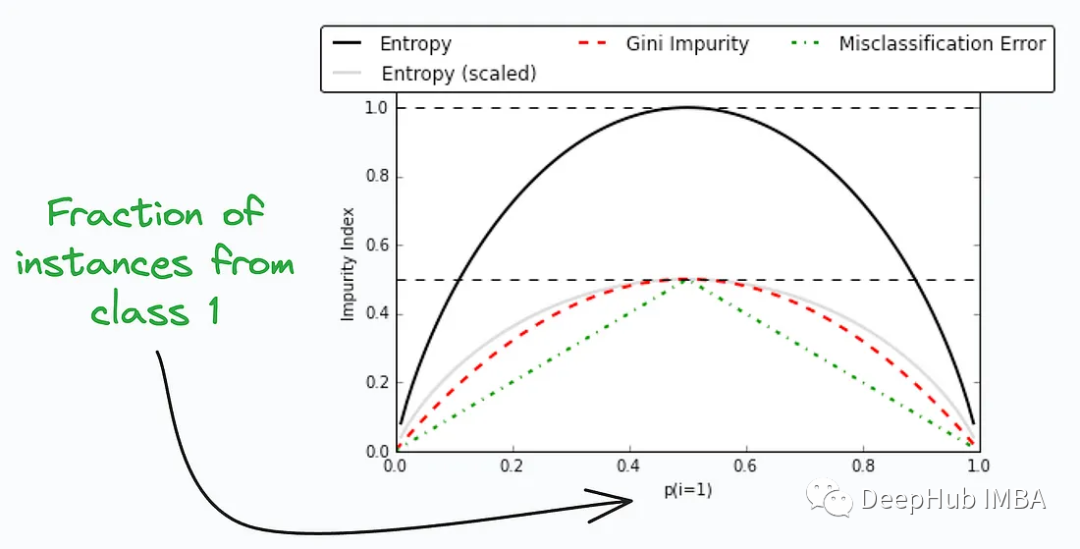
Gini Impurity et Entropy sont deux indicateurs couramment utilisés dans les algorithmes d'apprentissage automatique tels que les arbres de décision et les forêts aléatoires. Évaluez l'impureté des données et sélectionnez les propriétés de fractionnement optimales. Ils sont tous deux utilisés pour mesurer la quantité de fouillis dans un ensemble de données afin d'aider les arbres de décision à choisir comment diviser les données.

Ils sont utilisés pour mesurer l'impureté ou le désordre d'un nœud ou d'une scission dans un arbre de décision. La figure ci-dessus compare l'impureté et l'entropie de Gini à différentes divisions, ce qui peut donner un aperçu des compromis entre ces mesures.

Les deux sont des indicateurs valables pour la sélection de fractionnement de nœuds dans les algorithmes d'apprentissage automatique tels que les arbres de décision, mais celui à choisir dépend du problème spécifique et des caractéristiques des données.

10, Compromis biais-variance

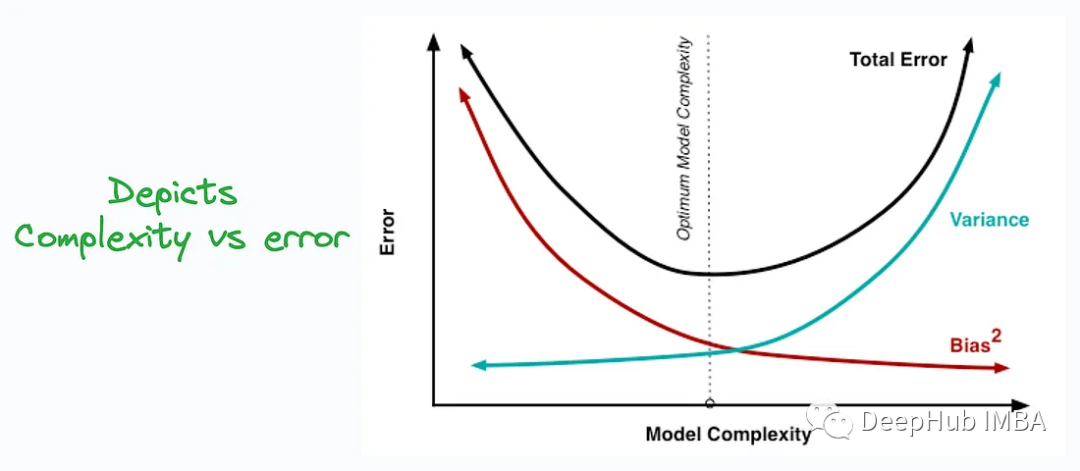
Le compromis biais-variance (compromis biais-variance) est un concept important dans l'apprentissage automatique, utilisé pour expliquer la différence entre les performances prédictives et la capacité de généralisation du modèle équilibre.

Il existe un compromis entre biais et variance. Lors de la formation d'un modèle d'apprentissage automatique, l'augmentation de la complexité du modèle diminue généralement le biais mais augmente la variance, tandis que la diminution de la complexité du modèle diminue la variance mais augmente le biais. Par conséquent, il existe un compromis où le modèle est à la fois capable de capturer des modèles dans les données (réduction du biais) et de montrer des prédictions stables sur différentes données (réduction de la variance).

Comprendre le compromis biais-variance aide les praticiens de l'apprentissage automatique à mieux créer et ajuster des modèles pour obtenir de meilleures performances et de meilleures capacités de généralisation. Il met en évidence la relation entre la complexité du modèle et la taille de l'ensemble de données, ainsi que la manière d'éviter le sous-apprentissage et le surapprentissage.

11. Tracés de dépendances partielles :

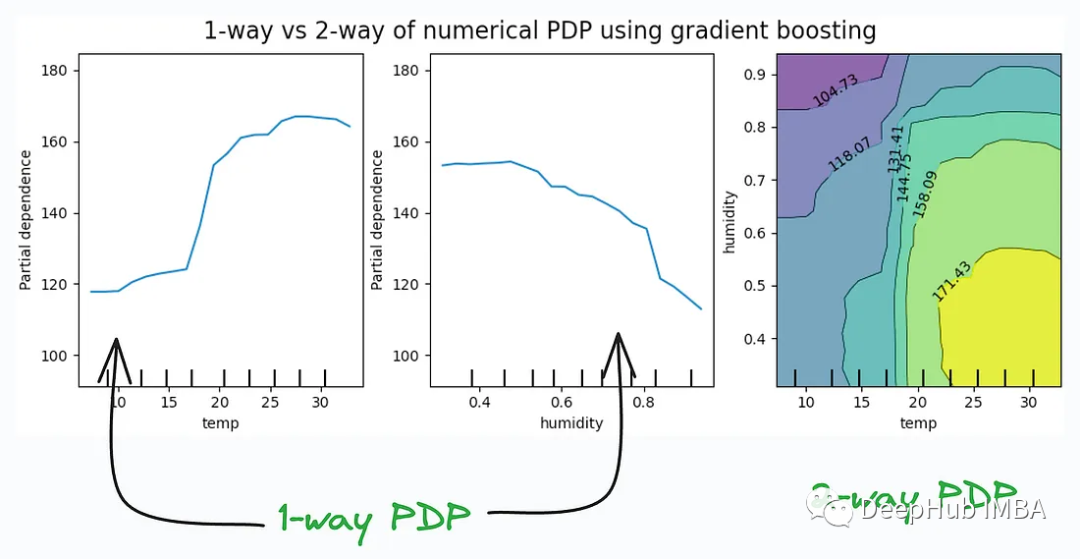
Les tracés de dépendances partielles (tracés de dépendances partielles) sont un outil pour visualiser et expliquer les modèles d'apprentissage automatique, particulièrement utiles pour comprendre l'impact des caractéristiques individuelles sur les prédictions du modèle. Ces graphiques aident à révéler la relation entre les fonctionnalités et les variables cibles pour mieux comprendre le comportement et les décisions du modèle.

Les tracés de dépendances partielles sont souvent utilisés avec des outils et des techniques d'interprétation, tels que les valeurs SHAP, LIME, etc., pour aider à expliquer les prédictions des modèles d'apprentissage automatique en boîte noire. Ils fournissent une visualisation qui permet aux data scientists et aux analystes de comprendre plus facilement les relations entre les décisions et les fonctionnalités d'un modèle.

Résumé

Ces graphiques couvrent les outils et concepts de visualisation couramment utilisés dans les domaines de l'analyse des données et de l'apprentissage automatique, qui aident à évaluer et à expliquer les performances du modèle, à comprendre la distribution des données et à sélectionner les meilleurs paramètres et modèles. Complexité, et l'impact des fonctionnalités d'insight sur les prédictions.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!