Tao Zhexuan se lance avec Copilot : Incroyable, il peut deviner la direction que je veux à partir du nom du théorème

Après avoir essayé GPT-4, Tao Zhexuan a de nouveau utilisé Github Copilot.

Cette fois, son scénario d'essai consiste à apprendre le langage Lean et à l'utiliser pour formaliser des théorèmes mathématiques.

Pour les grands modèles, la démonstration formelle du théorème est également un défi. Une preuve formelle est essentiellement un programme informatique, mais contrairement aux programmes traditionnels en C++ ou Python, l'exactitude de la preuve peut être vérifiée à l'aide d'assistants de preuve tels que le langage Lean. La démonstration de théorèmes est une forme particulière de génération de code qui est très stricte dans son évaluation et ne laisse aucune place aux illusions dans le modèle.

Le théorème mentionné par Terence Tao vient d'un article du 9 octobre :

La preuve dans l'article fait moins d'une page, mais la preuve formelle de Terence Tao utilise 200 lignes de langage Lean.

Par exemple, dans l'article Terence Tao affirme simplement que pour tout a>0, est convexe en nombres réels, car il s'agit d'un exercice de calcul régulier, puis appelle l'inégalité de Jensen, mais écrit tous les détails. Cela a pris environ 50 lignes de code.

Tao Zhexuan a déclaré que la capacité du copilote de Github à prédire correctement plusieurs lignes de code pour diverses vérifications de routine et à déduire la direction qu'il souhaite à partir d'indices tels que les noms des théorèmes est "incroyable".

La stratégie de « réécriture » du Lean est indispensable pour modifier des hypothèses ou des objectifs longs avec des substitutions ciblées qui opèrent sur des expressions sans avoir à les saisir intégralement.

"Lorsque j'écris des preuves dans LaTeX, je simule souvent grossièrement cette méthode en coupant et en collant la longue expression que je traite d'une ligne à l'autre, puis en effectuant des modifications ciblées, mais cela entraîne parfois des fautes de frappe. Elle est répartie sur plusieurs lignes dans le document, il est donc bon de pouvoir le réécrire de manière automatique et vérifiable "

Le document mentionne également une inégalité, c'est-à-dire que pour tout k, l, n, si est satisfait, alors

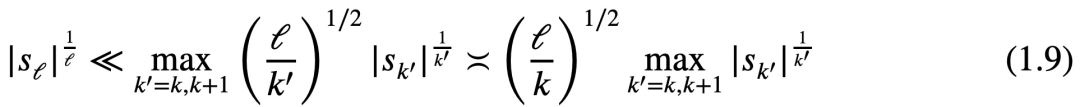Tao Zhexuan a dit que le prochain objectif est d'établir une version simple de cette inégalité, qui est l'inégalité (1,8) dans l'article :

Cette partie de la preuve utilise principalement la connaissance du calcul, mais une difficulté est la nécessité d'utiliser des symboles asymptotiques. Tao Zhexuan a déclaré que même si la démonstration ultérieure prendra beaucoup de temps, elle n'est pas particulièrement difficile.

Mais les outils actuels ont encore certaines limites, par exemple, la réécriture d'expressions impliquant des variables liées (telles que des variables de somme dans une séquence) n'est pas toujours facile à réaliser. Il attend avec impatience le jour où l'on pourra simplement demander à un LLM en langage naturel d'effectuer de telles transformations...

^{Lien de référence : https://mathstodon.xyz/@tao/111271244206606941}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!