Maison >Périphériques technologiques >IA >Aperçu de la multiplication matricielle d'un point de vue 3D, voici à quoi ressemble la pensée de l'IA
Aperçu de la multiplication matricielle d'un point de vue 3D, voici à quoi ressemble la pensée de l'IA
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-10-16 08:09:01993parcourir
Si le processus d'exécution de la multiplication matricielle peut être affiché en 3D, il ne sera pas si difficile d'apprendre la multiplication matricielle à l'époque.
De nos jours, la multiplication matricielle est devenue la pierre angulaire des modèles d'apprentissage automatique et la base de diverses technologies d'IA puissantes. Comprendre sa méthode d'exécution nous aidera certainement à comprendre plus profondément cette IA et ce monde de plus en plus intelligent.
Cet article du blog PyTorch présentera mm, un outil de visualisation pour la multiplication matricielle et la combinaison de multiplication matricielle.
Parce que mm utilise les trois dimensions spatiales, par rapport aux graphiques bidimensionnels habituels, mm aide à afficher et à stimuler intuitivement les idées, et utilise moins de surcharge cognitive, en particulier (mais sans s'y limiter)) pour les personnes douées en visuel et spatial. pensée.
Et avec trois dimensions pour combiner les multiplications matricielles, ainsi que la possibilité de charger des poids entraînés, mm peut visualiser de grandes expressions composées (telles que les têtes d'attention) et observer leurs modèles de comportement réels.
mm est entièrement interactif, s'exécute dans un iframe de navigateur ou de bloc-notes et enregistre l'état complet dans l'URL, le lien est donc une session partageable (les captures d'écran et les vidéos de cet article ont un lien, disponible sur Ouvrir la visualisation correspondante dans cet outil, veuillez vous référer au blog original pour plus de détails). Ce guide de référence décrit toutes les fonctionnalités disponibles.
Adresse de l'outil : https://bhosmer.github.io/mm/ref.html
Texte original du blog : https://pytorch.org/blog/inside-the-matrix
This Cet article est le premier dans lequel je présenterai les méthodes de visualisation, développerai l'intuition en visualisant quelques multiplications et expressions matricielles simples, puis plongerai dans quelques exemples étendus :
Introduction : Pourquoi cette visualisation est-elle meilleure ?
Échauffement : Animation - Découvrez comment fonctionne la décomposition canonique par multiplication matricielle
Échauffement : Expressions - Un aperçu rapide de quelques éléments de base des expressions
En profondeur dans la tête de l'attention : Examen approfondi avec NanoGPT Structure, valeurs et comportement informatique d'une paire de têtes d'attention pour GPT-2
Paralléliser l'attention : visualisez la parallélisation des têtes d'attention à l'aide d'exemples tirés du récent article Blockwise Parallel Transformer.
Taille de la couche d'attention : lorsque nous visualisons l'ensemble de la couche d'attention comme une structure unique, à quoi ressemblent ensemble la moitié MHA et la moitié FFA de la couche d'attention ? Comment l’image change-t-elle pendant le processus de décodage autorégressif ?
LoRA : Une explication visuelle détaillée de cette architecture de tête d'attention
1 Introduction
L'approche de visualisation de mm est basée sur le principe que la multiplication matricielle est essentiellement une opération tridimensionnelle.
En d'autres termes :
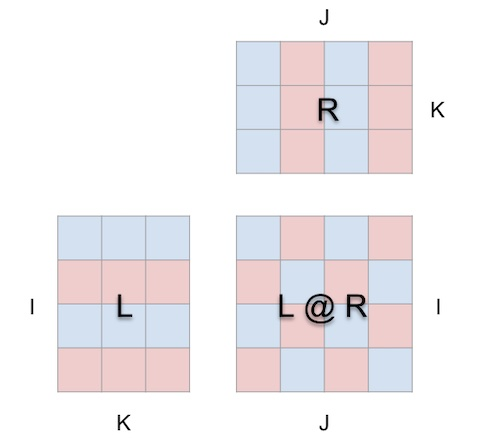
peut en fait être représenté comme ceci :

Lorsque nous enveloppons ainsi la multiplication matricielle dans un cube, entre la forme du paramètre, la forme du résultat et la dimension partagée. Les relations correctes sont tous en place.
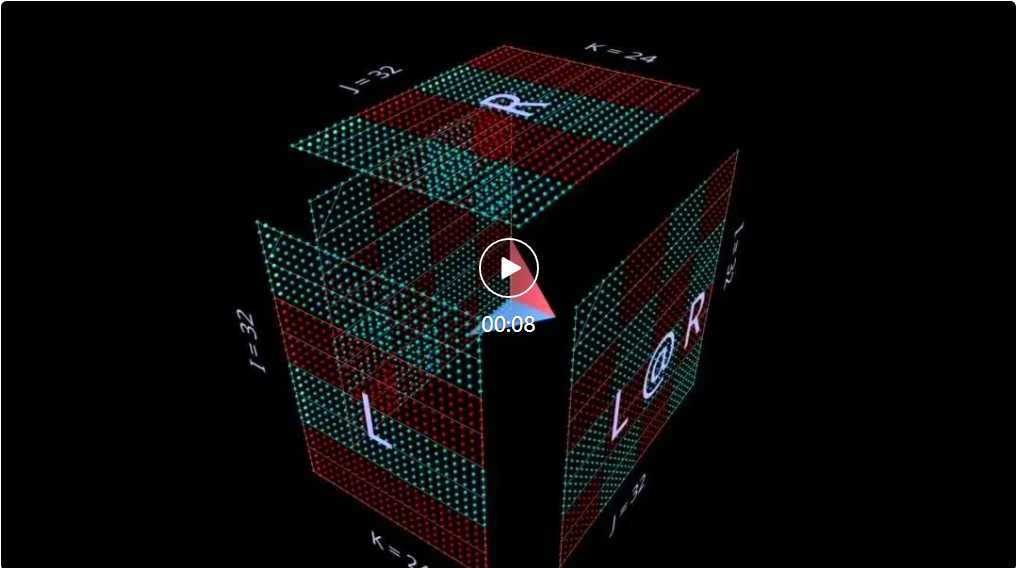
Maintenant, le calcul de multiplication matricielle a un sens géométrique : chaque position i, j dans la matrice résultante ancre un vecteur courant le long de la dimension de profondeur k à l'intérieur du cube, qui s'étend à partir de la i-ème rangée de L. Le plan horizontal de coupe la verticale plan s'étendant à partir de la jème colonne de R. Le long de ce vecteur, des paires d'éléments (i, k) (k, j) des arguments gauche et droit se rencontrent et sont multipliées, et les produits résultants sont additionnés le long de k et placés dans i du résultat, position j.
C'est la signification intuitive de la multiplication matricielle :
1. Projetez deux matrices orthogonales à l'intérieur d'un cube ;
2 Multipliez une paire de valeurs à chaque intersection pour obtenir une grille de produits ; Faites la somme le long de la troisième dimension orthogonale pour produire la matrice résultante.
Pour la direction, l'outil affiche une flèche à l'intérieur du cube pointant vers la matrice de résultat, avec une écriture bleue à partir du paramètre de gauche et une écriture rouge à partir du paramètre de droite. L'outil affiche également des lignes indicatrices blanches pour indiquer l'axe des lignes de chaque matrice, bien que ces lignes soient floues dans cette capture d'écran.
Les contraintes de mise en page sont simples et directes :
- Les paramètres et résultats de gauche doivent être adjacents le long de leur dimension de hauteur (i) partagée
- Les paramètres et résultats de droite doivent être adjacents le long de leur largeur partagée (j) dimension
- Les paramètres gauche et droit doivent être adjacents le long de leur dimension commune (largeur gauche / hauteur droite), qui devient la dimension profondeur (k) de la multiplication matricielle
- Cette représentation géométrique peut être utilisée pour visualiser tout La factorisation matricielle standard fournit une base solide et une base intuitive pour explorer des combinaisons non triviales de multiplications matricielles complexes, comme nous le verrons ensuite.
Avant de plonger dans des exemples plus complexes, jetons un coup d'œil à ce à quoi ressemble ce style de visualisation pour construire une compréhension intuitive de l'outil.
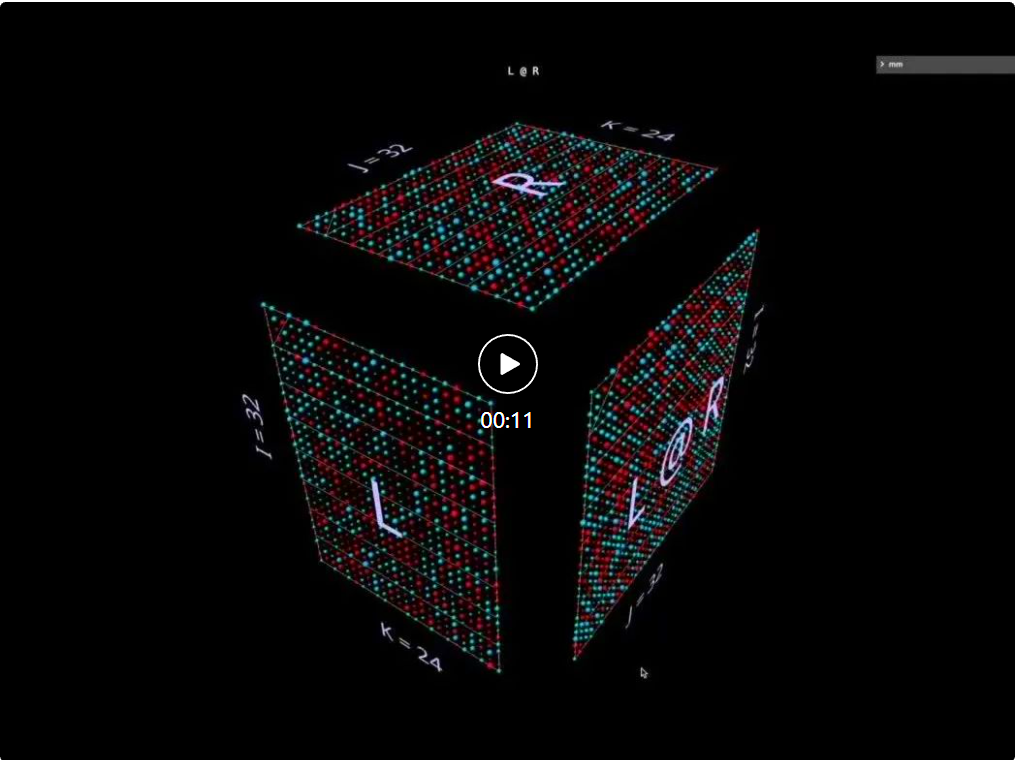
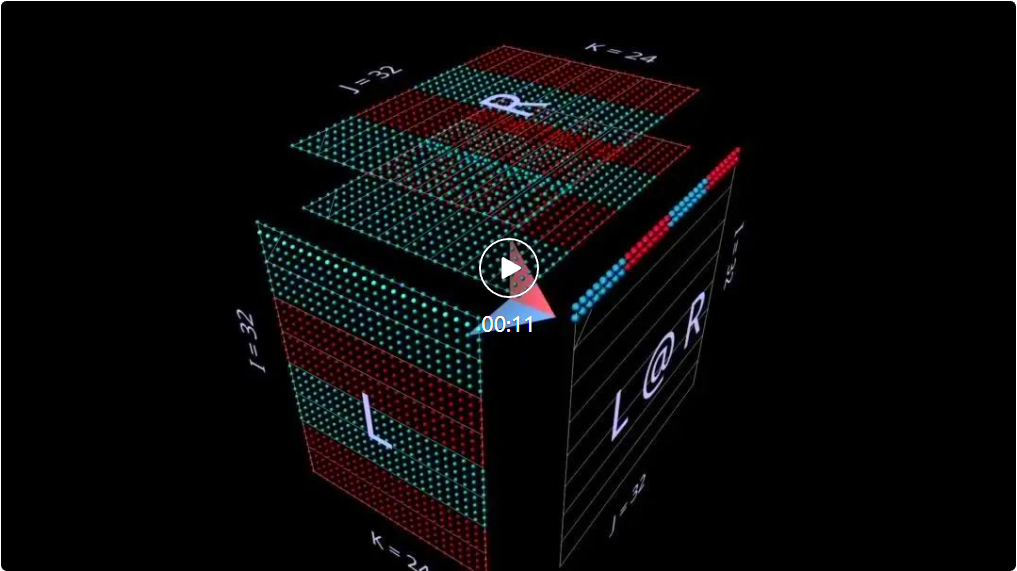
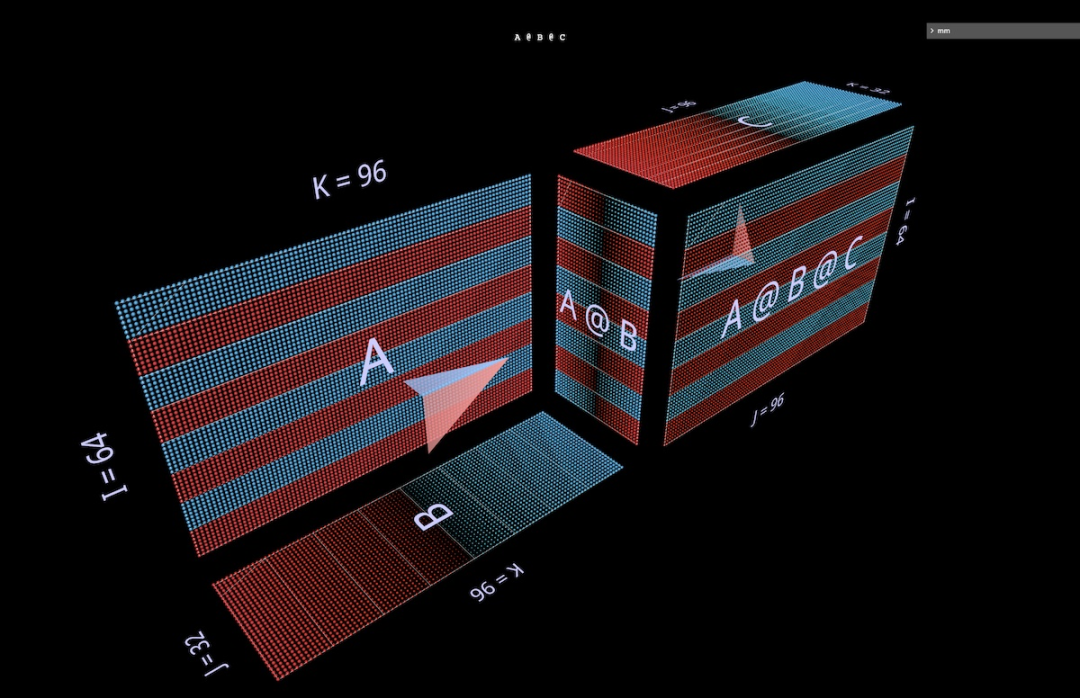
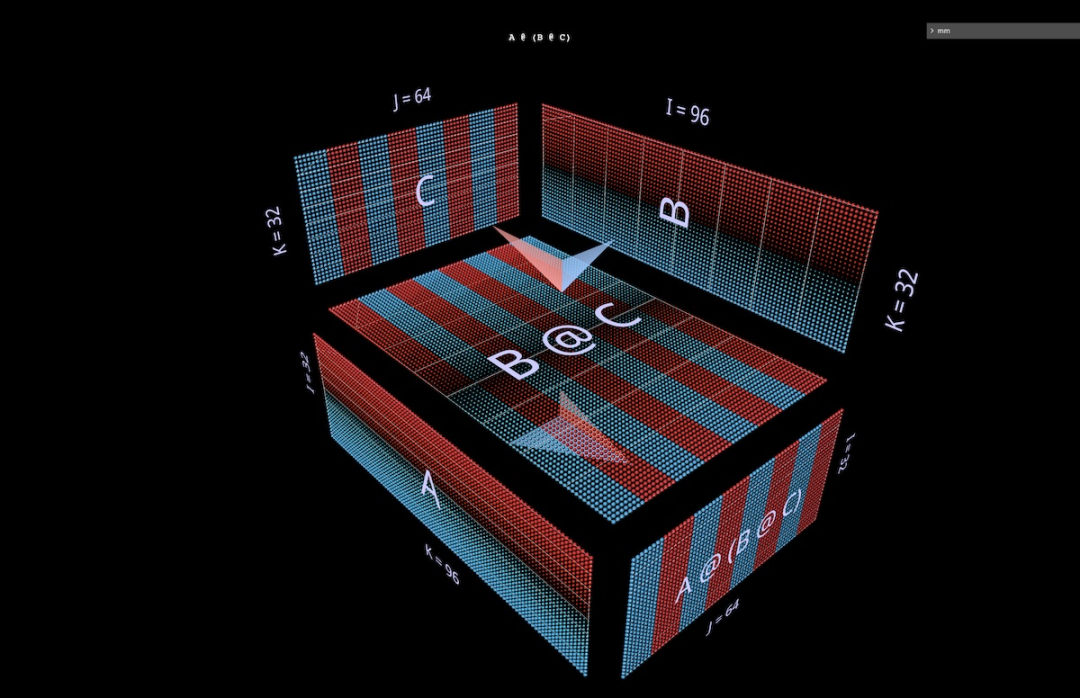
2a produit scalaireTout d'abord, examinons un algorithme classique : calculez chaque élément de résultat en calculant le produit scalaire de la ligne de gauche et de la colonne de droite correspondantes. Comme vous pouvez le voir sur l'animation ici, le vecteur de valeur multipliée parcourt l'intérieur du cube, fournissant à chaque fois un résultat additionné à l'emplacement correspondant. Ici, L a des blocs de lignes remplis de 1 (bleu) ou -1 (rouge) ; R a des blocs de colonnes remplis de la même manière. Ici, k vaut 24, donc la matrice résultante (L @ R) a des valeurs bleues de 24 et des valeurs rouges de -24. 2b Produit matrice-vecteur décomposé en produit matrice-vecteur La multiplication matricielle ressemble à un plan vertical (le produit de chaque colonne du paramètre gauche et du paramètre droit) lorsqu'elle balaie horizontalement l'intérieur de le cube , tracez les colonnes sur le résultat : Il peut être intéressant d'observer les valeurs intermédiaires d'une décomposition, même si l'exemple est simple. À titre d'exemple, notez que le produit matrice-vecteur au milieu met en évidence le motif vertical lorsque nous utilisons des paramètres initialisés aléatoirement - cela reflète le fait que chaque valeur intermédiaire est une copie à l'échelle des colonnes du paramètre de gauche : 2c Vector - Produit matriciel se décompose en un vecteur - La multiplication matricielle des produits matriciels ressemble à un plan horizontal qui dessine des lignes sur le résultat lorsqu'il passe à l'intérieur du cube : Commutation aux paramètres initialisés aléatoirement, vous pouvez voir un modèle similaire au produit matrice-vecteur - seulement cette fois en mode horizontal, correspondant au fait que chaque produit vecteur-matrice intermédiaire est une copie à l'échelle des lignes du paramètre de droite. Lorsque l'on réfléchit à la façon dont la multiplication matricielle représente la structure rang-somme de ses paramètres, une approche utile consiste à imaginer ces deux modes se produisant simultanément dans le calcul : 2d Sommation des produits externes La décomposition du troisième plan est le long de l'axe k, les résultats de la multiplication matricielle sont calculés en additionnant ponctuellement les produits extérieurs vectoriels. Ici, nous pouvons voir que le plan produit extérieur balaie le cube "de l'arrière vers l'avant", s'accumulant dans le résultat : En utilisant une matrice initialisée aléatoirement pour cette décomposition, nous pouvons non seulement voir les valeurs, mais aussi les résultats Les rangs de s'accumulent au fur et à mesure que chaque produit extérieur de rang 1 y est ajouté. Cela explique également intuitivement pourquoi la « factorisation de bas rang » (c'est-à-dire l'approximation d'une matrice en construisant une multiplication matricielle avec des paramètres plus petits dans la dimension de profondeur) fonctionne mieux lorsque la matrice approchée est une matrice de bas rang. C'est LoRA qui sera évoqué plus tard : 3 Échauffement : Expressions De quelles manières peut-on étendre cette méthode de visualisation à la décomposition des multiplications matricielles ? L'exemple précédent visualisait une multiplication matricielle unique L @ R des matrices L et R, mais que se passerait-il si L et/ou R étaient eux-mêmes des multiplications matricielles ? Il s'avère que cette approche s'adapte bien aux expressions composées. La règle clé est simple : la multiplication de la sous-expression (sous)matrice est un autre cube soumis aux mêmes contraintes de disposition que la multiplication de la matrice parent ; la face résultat de la multiplication de la sous-matrice est également la face paramètre de la multiplication de la matrice parent, tout comme une multiplication covalente ; Électrons partagés. Dans ces contraintes, nous pouvons organiser différents aspects de la multiplication de sous-matrices en fonction de nos propres besoins. Le schéma par défaut de l'outil est utilisé ici, qui produit une alternance de cubes convexes et concaves. Cette disposition fonctionne bien dans la pratique, maximisant l'espace tout en minimisant l'occlusion. (Mais la mise en page est entièrement personnalisable, voir la page des outils mm pour plus de détails.) Cette section visualisera certains des éléments constitutifs clés des modèles d'apprentissage automatique afin que les lecteurs puissent se familiariser avec cette représentation visuelle et en tirer de nouvelles intuitions. 3a Expressions associatives de gauche Deux expressions de la forme (A @ B) @ C seront présentées ci-dessous, chacune avec sa propre forme et ses caractéristiques uniques. (Remarque : mm suit la convention selon laquelle la multiplication matricielle reste associative, donc (A @ B) @ C peut simplement être écrit comme A @ B @ C.) Donnez d'abord à A @ B @ C une forme FFN très distinctive, où La « dimension cachée » est plus large que la dimension « d’entrée » ou « de sortie ». (Plus précisément, pour cet exemple, cela signifie que la largeur de B est supérieure à la largeur de A ou C.) Comme l'exemple de multiplication à matrice unique, la flèche flottante pointe vers la matrice résultante, où l'empreinte bleue provient du argument de gauche, l'empreinte rouge provient des paramètres de droite. Et lorsque la largeur de B est inférieure à la largeur de A ou C, il y aura un goulot d'étranglement dans la visualisation de A @ B @ C, semblable à la forme d'un auto-encodeur. Le modèle de modules de bosses alternés peut également être étendu à des chaînes de longueurs arbitraires : Par exemple, ce goulot d'étranglement multicouche : 3b Expression associative correcte Visualisez ensuite l'expression associative correcte A @ (B@C). Semblable à l'expansion horizontale d'une expression associative gauche - on peut dire qu'elle part du paramètre gauche de l'expression racine, la chaîne d'expression associative droite est étendue verticalement, en commençant par le paramètre droit de l'expression racine. On peut parfois voir un MLP formé sous une forme de combinaison à droite, où le côté droit est l'entrée en colonnes et la couche de poids s'étend de droite à gauche. En utilisant la matrice de l'exemple FFN à deux couches décrit ci-dessus (après transposition appropriée), cela ressemblerait à ceci, C est maintenant l'entrée, B est la première couche et A est la deuxième couche : Aussi, à l'exception de la couleur d'empennage (bleu à gauche, rouge à droite), le deuxième repère visuel pour distinguer les paramètres gauche et droit est leur orientation : les lignes de paramètres à gauche sont coplanaires aux lignes de résultats - elles sont le long le même axe (i) Empilé. Par exemple (B @ C) ci-dessus, les deux indices peuvent nous indiquer que B est le paramètre de gauche. 3c Expressions binaires Pour que les outils de visualisation, pour être utiles, ils doivent non seulement être utilisés pour des exemples pédagogiques simples, mais aussi être facilement utilisés pour des expressions plus complexes. Dans les cas d'utilisation réels, un composant structurel clé est une expression binaire : une multiplication matricielle avec des sous-expressions sur les côtés gauche et droit. L'expression la plus simple de la forme (A @ B) @ (C @ D) est visualisée ici : 3d Une petite note : Partitionnement et parallélisme Une élaboration complète de ce sujet est au-delà de ceci C'est la portée de cet article, mais nous verrons son utilité pratique plus tard dans la section principale de l'attention. Mais pour vous réchauffer, regardez deux exemples simples pour voir comment ce style de visualisation peut rendre le raisonnement sur des expressions composées parallélisées très intuitif, simplement grâce à un simple partitionnement géométrique. Le premier exemple consiste à appliquer un partitionnement « parallèle aux données » typique à l'exemple de goulot d'étranglement multicouche de jointure gauche ci-dessus. Nous partitionnons selon i, en segmentant le paramètre initial de gauche (le "lot") et tous les résultats intermédiaires (les "activations"), mais pas les paramètres suivants (les "poids") - cette géométrie rend l'expression Il devient évident lequel les acteurs sont segmentés et qui restent intacts : Le deuxième exemple est difficile à comprendre intuitivement sans support géométrique clair : il montre comment exprimer la sous-expression de gauche en Paralléliser une expression binaire en partitionnant l'expression, partitionnant l'enfant de droite expression le long de l'axe i et partitionnement de l'expression parent le long de l'axe k : 4 Plonger profondément dans la tête d'attention Jetons maintenant un coup d'œil à la tête d'attention de GPT-2 - en particulier la configuration "gpt2" (petite) de la 4ème tête de la 5ème couche de NanoGPT (nombre de couches = 12, nombre de têtes = 12, nombre d'intégrations = 768), en utilisant les poids d'OpenAI via HuggingFace. Les activations d'entrée sont extraites d'une transmission directe sur l'exemple de formation OpenWebText contenant 256 jetons. Il n'y a rien de spécial à propos de cette tête en particulier, elle a été choisie principalement parce qu'elle calcule un modèle d'attention très courant et elle est située au milieu du modèle où les activations se sont structurées et montrent des textures intéressantes. 4a Structure Cette tête d'attention complète est visualisée comme une expression composée unique, qui commence à partir de l'entrée et se termine par la sortie projetée. (Remarque : pour garantir l'autosuffisance, la projection de sortie est effectuée pour chaque tête comme décrit ici pour Megatron-LM.) Ce calcul contient six multiplications matricielles : Une brève description de ce qui est fait ici : Les pales du moulin à vent sont des multiplications matricielles 1, 2, 3 et 6 : les premiers ensembles sont les projections internes des entrées de Q, K et V ; les secondes sont les projections externes de attn @ V vers le dimension d'intégration. Il y a deux multiplications matricielles au centre : la première calcule les scores d'attention (le cube convexe à l'arrière) puis les utilise pour obtenir le jeton de sortie (le cube concave à l'avant) en fonction du vecteur de valeur. La causalité signifie que les scores d’attention forment un triangle inférieur. Mais il serait préférable que les lecteurs explorent eux-mêmes cet outil en détail, plutôt que de simplement regarder des captures d'écran ou la vidéo ci-dessous, afin de le comprendre plus en détail – à la fois sa structure et les valeurs réelles qui y circulent. le processus de calcul. 4b Calcul de la valeur de la somme Voici l'animation du processus de calcul de la tête d'attention. Plus précisément, nous examinons (c'est-à-dire les multiplications matricielles 1, 4, 5 et 6 ci-dessus, où K_t et V sont pré-calculés) sont calculées comme une chaîne fusionnée de produits vectoriels-matrices : chacun dans la séquence Each l’élément passe par l’attention de l’entrée à la sortie en une seule étape. D'autres options pour cette animation seront abordées plus loin dans la section sur la parallélisation, mais voyons d'abord ce que nous disent les valeurs calculées. Nous pouvons voir beaucoup de choses intéressantes : Avant de discuter du calcul de l'attention, vous pouvez voir à quel point la forme de Q et K_t de bas rang est étonnante. En zoomant sur l'animation du produit à matrice vectorielle Q @ K_t, elle semble encore plus vivante : le grand nombre de canaux (positions intégrées) dans Q et K semblent être plus ou moins constants dans la séquence, ce qui signifie qu'un signal d'attention utile peut être généré uniquement par un petit ensemble de pilotes intégrés. Comprendre et exploiter ce phénomène fait partie du projet d'efficacité des transformateurs SysML ATOM. Les gens sont peut-être plus familiers avec les diagonales puissantes mais imparfaites qui apparaissent dans la matrice d'attention. Il s'agit d'un schéma courant qui apparaît dans de nombreuses têtes d'attention de ce modèle (et dans de nombreux Transformers). Cela peut générer une attention locale : le jeton de valeur dans le petit quartier immédiatement avant la position du jeton de sortie détermine en grande partie le modèle de contenu du jeton de sortie. Cependant, la taille de ce quartier et l'influence des jetons individuels en son sein varient considérablement - cela peut être vu dans le gel hors diagonale dans la grille d'attention, ainsi que dans la matrice d'attention descendant le long de la séquence attn [i ] @ V vecteur - Le motif d'onde vu dans le plan du produit matriciel. Mais notez que le voisinage local n'est pas la seule chose à noter : la colonne la plus à gauche de la grille d'attention (correspondant au premier token de la séquence) est entièrement remplie de valeurs non nulles (mais fluctuantes), ce qui signifie que chaque jeton de sortie sera affecté dans une certaine mesure par le premier jeton de valeur. De plus, il existe une oscillation imprécise mais perceptible dans la dominance du score d'attention entre le quartier du jeton actuel et le jeton initial. La période de cette oscillation varie, mais elle commence généralement brièvement, puis s'allonge à mesure que vous avancez dans la séquence (de même, étant donné la relation causale, le nombre de jetons d'attention candidats par ligne est lié). Afin de comprendre comment (attn @ V) se forme, il est important de ne pas se concentrer uniquement sur l'attention – V est tout aussi important. Chaque terme de sortie est une moyenne pondérée de l'ensemble du vecteur V : dans le cas extrême où l'attention est une diagonale parfaite, attn @ V n'est qu'une copie exacte de V . Ici, nous voyons quelque chose de plus texturé : des structures visibles en forme de bande où un jeton particulier obtient un score élevé sur une sous-séquence contiguë de lignes d'attention, superposées à une matrice clairement similaire à V, mais avec des diagonales plus épaisses. Il y a une certaine occlusion verticale. (Remarque : selon le guide de référence mm, un appui long ou un contrôle-clic affichera la valeur numérique réelle de l'élément visuel.) N'oubliez pas que puisque nous sommes dans la couche intermédiaire (couche 5), l'entrée de cette tête d'attention est une représentation intermédiaire, pas le texte tokenisé d'origine. Les motifs observés dans l'entrée suscitent donc en eux-mêmes la réflexion - en particulier, les lignes verticales fortes sont des positions d'intégration spécifiques dont les valeurs ont uniformément une amplitude élevée sur de longues périodes de la séquence - parfois presque pleines. Mais ce qui est intéressant, c'est que le premier vecteur de la séquence d'entrée est unique, brisant non seulement le modèle de ces colonnes de haute amplitude, mais portant également des valeurs atypiques à presque toutes les positions (remarque : non visualisé ici, mais ce modèle se reproduit sur plusieurs échantillons d'entrées). Remarque : Concernant les deux derniers points, il convient de rappeler que ce qui est visualisé ici est un calcul sur un seul échantillon d'entrée. En pratique, on constate que chaque tête possède un modèle caractéristique qui est exprimé de manière cohérente (bien que non identique) sur un ensemble assez large d'échantillons, mais lorsque l'on regarde une visualisation contenant des activations, il faut se rappeler que la distribution complète de l'entrée peut affecter de manière subtile les idées et les intuitions qu’il inspire. Enfin, il est à nouveau recommandé d'explorer directement l'animation ! 4c Il y a beaucoup de différences intéressantes avec les têtes d'attention Avant de continuer, voici une autre démonstration montrant l'utilité de simplement étudier le modèle pour comprendre son fonctionnement en détail. C'est un autre chef d'attention de GPT-2. Son modèle de comportement est assez différent de celui de Level 5 Head 4 - comme on pouvait s'y attendre puisqu'il se trouve dans une partie très différente du modèle. Cet en-tête est situé au niveau 1 : Tête 2 du niveau 0 : Points remarquables : L'attention de cet en-tête est très uniformément répartie. Cela a pour effet de fournir la moyenne relativement non pondérée de V (ou le préfixe causal approprié de V) à chaque ligne de attn@V, comme le montre l'animation : à mesure que nous descendons dans le triangle du score d'attention, attn[i] @ V ; vecteur - produit matriciel avec de petites fluctuations, plutôt qu'une simple copie réduite et progressivement révélée de V. attn @ V a une uniformité verticale étonnante - le même modèle de valeurs persiste tout au long de la séquence dans de grandes régions en colonnes qui y sont intégrées. On peut les considérer comme des propriétés partagées par chaque jeton. Remarque : d'une part, on pourrait s'attendre à ce que attn @ V ait une certaine cohérence, étant donné l'effet d'une répartition très uniforme de l'attention. Mais chaque ligne est constituée d'une sous-séquence causale de V plutôt que de la séquence entière - pourquoi cela ne conduirait-il pas à davantage de changements, comme une déformation progressive à mesure que vous avancez dans la séquence ? L'inspection visuelle montre que V n'est pas uniforme sur toute sa longueur, la réponse doit donc résider dans une propriété plus subtile de sa distribution de valeurs. Enfin, après projection externe, le rendement de cette tête devrait être plus uniforme dans le sens vertical. On peut avoir une forte impression : la plupart des informations véhiculées par cette tête d'attention sont constituées d'attributs partagés par chaque jeton de la séquence. La composition de ses pondérations de projection de production peut renforcer cette intuition. Dans l’ensemble, on ne peut s’empêcher de se demander : les informations extrêmement régulières et très structurées générées par cette tête d’attention ont peut-être été obtenues par des moyens informatiques légèrement… moins luxueux. Ce n’est certainement pas un domaine inexploré, mais la clarté et la richesse de la visualisation des signaux informatiques peuvent être extrêmement utiles à la fois pour générer de nouvelles idées et pour raisonner sur celles existantes. 4d Retour à l'introduction : invariants libres Avec le recul, il convient de le répéter : la raison pour laquelle nous sommes capables de visualiser des opérations de composition non triviales axées sur l'attention et de les garder intuitives est due à des propriétés algébriques importantes telles que les paramètres. une forme est contrainte ou quels axes parallèles se croisent avec quelles opérations), ces propriétés ne nécessitent aucune réflexion supplémentaire : elles découlent directement des propriétés géométriques de l'objet visuel, plutôt que de règles supplémentaires à retenir. Par exemple, dans ces visualisations de tête d'attention, on peut clairement voir : Q et attn @ V ont la même longueur, K et V ont la même longueur, et les longueurs de ces paires sont indépendantes les unes des autres ; Q a la même largeur que K, V a la même largeur que attn @ V, et les largeurs de ces paires sont indépendantes les unes des autres. Ces structures sont structurellement réelles, résultat simple de l'emplacement des composants structurels dans la structure composite et de leur orientation. Cet avantage de « nature libre » est particulièrement utile lors de l'exploration de variations sur des structures typiques - un exemple évident est le décodage d'une matrice d'attention élevée à une seule ligne dans un jeton autorégressif, un à la fois : 5 parallélisme Attention L'animation de la 4ème tête des 5 couches ci-dessus visualise 4 des 6 multiplications matricielles dans la tête d'attention. Ils sont visualisés comme une chaîne de fusion de produits vectoriels-matrices, confirmant une intuition géométrique : toute la chaîne de jonction à gauche, de l'entrée à la sortie, est superposée le long de l'axe i partagé et peut être parallélisée. 5a Exemple : Partition selon i Pour paralléliser le calcul en pratique, nous pouvons partitionner l'entrée en morceaux le long de l'axe i. Nous pouvons visualiser ce partitionnement dans l'outil en spécifiant qu'un axe donné soit divisé en un nombre spécifique de blocs - 8 sera utilisé dans ces exemples, mais ce nombre n'a rien de spécial. Au-delà de cela, cette visualisation montre clairement que chaque calcul parallèle nécessite le wQ complet (pour la projection interne), K_t et V (pour l'attention) et wO (pour la projection externe) car les dimensions non partitionnées de ces matrices sont adjacentes aux dimensions partitionnées. matrices : 5b Exemple : Double partitionnement Un exemple de partitionnement selon plusieurs axes est également donné ici. À cette fin, nous choisissons ici de visualiser une innovation récente dans ce domaine, à savoir Block Parallel Transformer (BPT), qui est basée sur certains résultats de recherche tels que Flash Attention. Veuillez vous référer à l'article : https://arxiv.org/. pdf/2305.19370.pdf Tout d'abord, BPT divise le long de i comme décrit ci-dessus - et étend en fait également cette partition horizontale de la séquence jusqu'à l'autre moitié de la couche d'attention (FFN). (Une visualisation de ceci sera présentée plus tard.) Pour résoudre pleinement ce problème de longueur de contexte, ajoutez une deuxième partition à MHA — la partition du calcul de l'attention lui-même (c'est-à-dire la partition le long de l'axe j de Q @ K_t). Ensemble, ces deux partitions divisent l'attention en une grille de blocs : Comme le montre clairement cette visualisation : Cette double partition résout efficacement le problème de longueur du contexte car nous pouvons désormais diviser visuellement la longueur de la séquence de chaque occurrence. dans le calcul de l'attention. La "plage" de la deuxième partition : Il ressort clairement de la structure géométrique que le calcul de projection interne de K et V peut être partitionné avec la multiplication matricielle double centrale. Notez un détail subtil : l'indice visuel ici est que nous pouvons également paralléliser la multiplication matricielle ultérieure attn @ V le long de k et additionner les résultats partiels dans le style split-k, parallélisant ainsi l'intégralité de la multiplication matricielle double. Mais softmax ligne par ligne dans sdpa() ajoute une exigence : chaque ligne doit avoir toute sa segmentation normalisée avant de calculer la ligne correspondante de attn@V, ce qui ajoute des étapes supplémentaires ligne par ligne. 6 Taille de la couche d'attention On sait que la première moitié de la couche d'attention (MHA) a des exigences de calcul élevées en raison de sa complexité quadratique, mais la seconde moitié (FFN) a également ses propres besoins, Cela est dû à la largeur de sa dimension cachée, qui est généralement 4 fois la largeur de la dimension intégrée du modèle. Visualiser la biomasse d’une couche d’attention complète permet de comprendre intuitivement comment les deux moitiés de la couche se comparent. 6a Visualiser la couche d'attention complète Ci-dessous se trouve une couche d'attention complète, avec la première moitié (MHA) à l'arrière et la seconde moitié (FFN) à l'avant. Encore une fois, la flèche pointe dans la direction du calcul. Remarque : Cette visualisation ne représente pas une seule tête d'attention, mais montre les poids Q/K/V non découpés et les projections autour de la double multiplication centrale de la matrice. Bien sûr, cela ne visualise pas fidèlement l'opération MHA complète - mais l'objectif ici est d'avoir une idée plus claire des tailles relatives des matrices dans les deux moitiés de la couche, plutôt que de la quantité relative de calcul effectuée par chaque moitié. (De plus, les poids ici utilisent des valeurs aléatoires au lieu de poids réels.) Les dimensions utilisées ici sont réduites pour garantir que le navigateur peut (relativement) le transporter, mais les proportions restent les mêmes (d'après la petite configuration de NanoGPT ) : Dimension d'intégration du modèle = 192 (à l'origine 768), dimension d'intégration FFN = 768 (à l'origine 3 072), longueur de séquence = 256 (à l'origine 1 024), bien que la longueur de la séquence n'ait aucun impact fondamental sur le modèle. (Visuellement, les changements dans la longueur de la séquence apparaîtront comme des changements dans la largeur de la lame d'entrée, entraînant des changements dans la taille du centre d'attention et la hauteur du plan vertical en aval.) 6b Visualisation de la couche de partitionnement BPT Il suffit de regarder en arrière le Blockwise Parallel Transformer, voici un schéma de parallélisation qui visualise BPT dans le contexte de l'ensemble de la couche d'attention (en-têtes omis comme ci-dessus). En particulier, notez comment le partitionnement le long de i (le bloc de séquence) s'étend à travers les moitiés MHA et FFN : 6c Partitionnement du FFN Cette méthode de visualisation suggère une partition supplémentaire orthogonale à celle décrite ci-dessus - sur la moitié FFN de la couche d'attention, divisez la multiplication matricielle double (attn_out @ FFN_1) @ FFN_2, d'abord le long de j attn_out @ FFN_1 , puis effectuez la multiplication matricielle suivante avec k avec FFN_2. Ce partitionnement divise les deux couches de poids FFN pour réduire les exigences de capacité pour chaque composant participant au calcul, au détriment de la sommation finale des résultats partiels. Voici à quoi ressemble cette méthode de partitionnement lorsqu'elle est appliquée à une couche d'attention non partitionnée : Voici à quoi elle ressemble lorsqu'elle est appliquée à une couche partitionnée BPT : Visualisation 6d, un jeton à la fois. processus Dans le processus de décodage autorégressif un jeton à la fois, le vecteur de requête se compose d'un seul jeton. Il est instructif d'imaginer dans votre esprit à quoi ressemblerait une couche d'attention dans ce cas : une seule ligne d'intégration traversant un immense plan de poids carrelé. En plus de souligner l'immensité des poids par rapport aux activations, cette vue rappelle également l'idée que K_t et V fonctionnent de manière similaire aux couches générées dynamiquement dans un MLP à 6 couches, malgré les calculs mux/Demux peuvent rendre cette correspondance imprécise : 7 LoRA Le récent article LoRA "LoRA: Low-Rank Adaptation of Large Language Models" décrit une technique de réglage fin efficace basée sur l'idée : les poids δ introduits lors du réglage fin sont de bas rang . Selon l'article, cela "nous permet d'entraîner indirectement certaines couches denses dans un réseau neuronal en optimisant la matrice de décomposition des rangs des changements de couches denses au cours de l'adaptation... tout en gardant les poids pré-entraînés gelés". Idée En bref, l'étape clé est d'entraîner les facteurs de la matrice de poids plutôt que la matrice elle-même : remplacer le tenseur de poids I x J par un tenseur I x K et une multiplication matricielle du tenseur K x J, où il est garanti que K est une petite valeur. La façon dont LoRA applique cette méthode de décomposition au processus de réglage fin est la suivante : 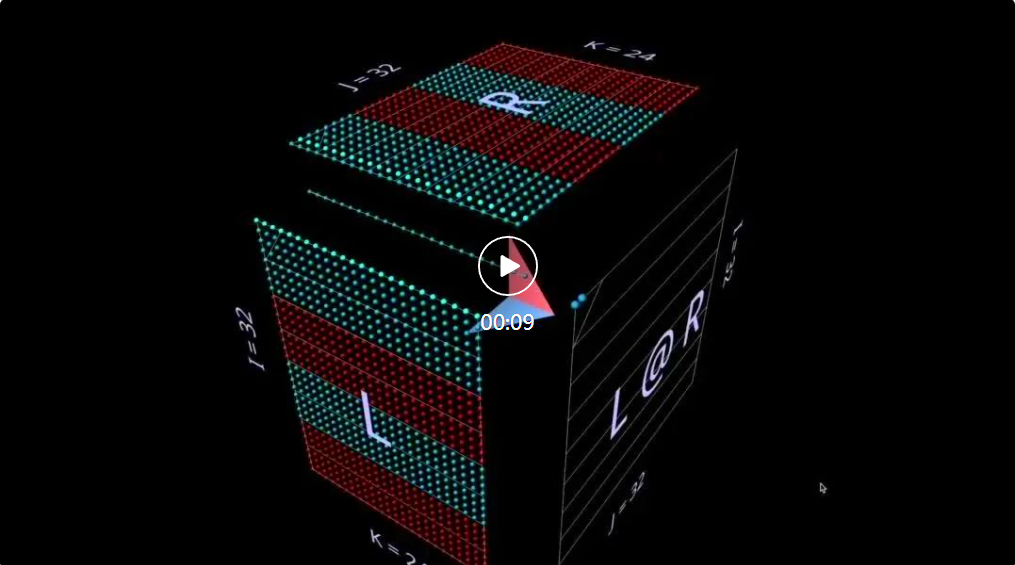

 En voici un autre qui utilise des produits vectoriels-matrices pour construire l'intuition. Exemple, ce qui montre que la matrice d'identité agit comme un miroir placé à un angle de 45 degrés, reflétant ses paramètres et résultats correspondants :
En voici un autre qui utilise des produits vectoriels-matrices pour construire l'intuition. Exemple, ce qui montre que la matrice d'identité agit comme un miroir placé à un angle de 45 degrés, reflétant ses paramètres et résultats correspondants : 






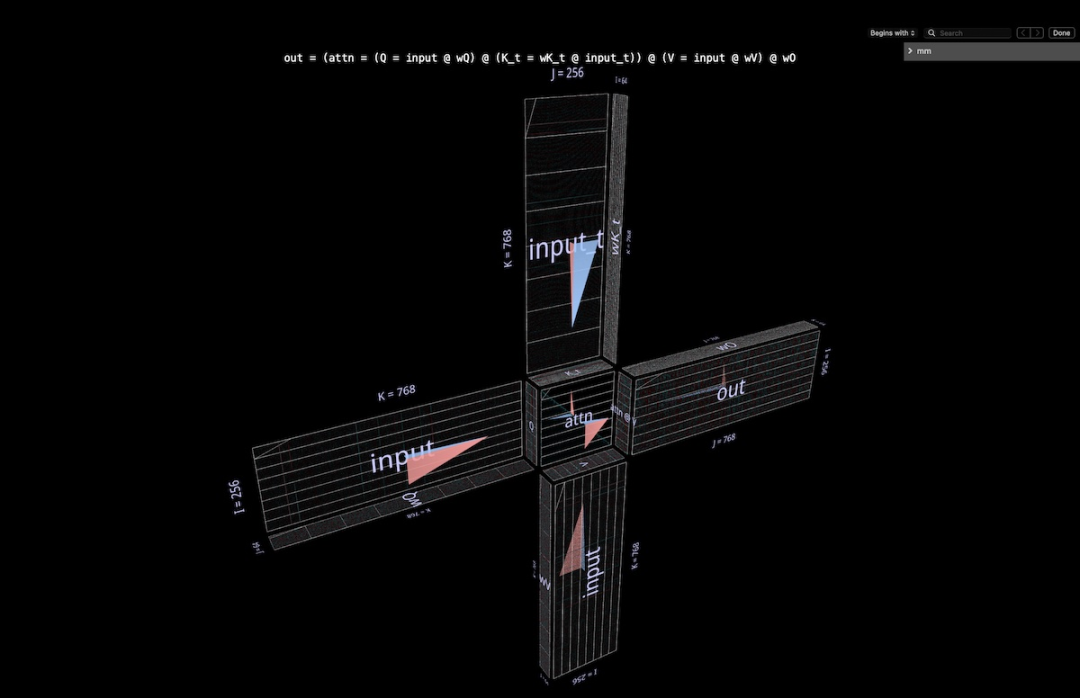
Q = input @ wQ// 1K_t = wK_t @ input_t// 2V = input @ wV// 3attn = sdpa(Q @ K_t)// 4head_out = attn @ V // 5out = head_out @ wO // 6
sdpa (input @ wQ @ K_t) @ V @ wO










 7b Appliquez LoRA à la tête d'attention
7b Appliquez LoRA à la tête d'attention
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

