Maison >Périphériques technologiques >IA >Grâce à MAmmoT, LLM devient un généraliste mathématique : de la logique formelle aux quatre opérations arithmétiques
Grâce à MAmmoT, LLM devient un généraliste mathématique : de la logique formelle aux quatre opérations arithmétiques
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-09-25 13:53:121545parcourir
Le raisonnement mathématique est une capacité importante des grands modèles de langage modernes (LLM). Malgré quelques progrès récents dans ce domaine, il existe encore un écart évident entre le LLM fermé et open source. Les modèles à source fermée tels que GPT-4, PaLM-2 et Claude 2 dominent sur les benchmarks de raisonnement mathématique courants tels que GSM8K et MATH, tandis que les modèles open source tels que Llama, Falcon et OPT sont nettement à la traîne sur tous les benchmarks
Pour résoudre Sur cette question, la communauté de recherche travaille dans deux directions
(1) Les méthodes de pré-formation continue telles que Galactica et MINERVA peuvent former en continu le LLM sur la base de plus de 100 milliards de données de réseau liées aux mathématiques. Cette méthode peut améliorer la capacité de raisonnement scientifique général du modèle, mais le coût de calcul est plus élevé
Méthodes de réglage précis des ensembles de données spécifiques telles que le réglage fin de l'échantillonnage par rejet (RFT) et WizardMath, qui utilisent les données supervisées d'un ensemble de données spécifique. pour peaufiner le LLM. Bien que ces méthodes puissent améliorer les performances dans un domaine spécifique, elles ne se généralisent pas à des tâches de raisonnement mathématique plus larges au-delà du réglage fin des données. Par exemple, RFT et WizardMath peuvent améliorer la précision de plus de 30 % sur GSM8K (dont l'un est un ensemble de données affiné), mais nuire à la précision sur des ensembles de données en dehors du domaine tels que MMLU-Math et AQuA, ce qui la rend plus faible. jusqu'à 10 %
Récemment, des équipes de recherche d'institutions telles que l'Université de Waterloo et l'Ohio State University ont proposé une méthode de réglage fin de l'enseignement mathématique légère mais généralisable qui peut être utilisée pour améliorer la généralité du LLM (c'est-à-dire non limité aux tâches de mise au point) capacité de raisonnement mathématique.
Contenu réécrit : dans le passé, la méthode de concentration était principalement la méthode de la chaîne de pensée (CoT), qui consiste à résoudre des problèmes mathématiques à travers une description étape par étape en langage naturel. Cette méthode est très générale et peut être appliquée à la plupart des disciplines mathématiques, mais il existe certaines difficultés liées à la précision des calculs et aux processus de raisonnement mathématique ou algorithmique complexes (tels que la résolution des racines d'équations quadratiques et le calcul des valeurs propres matricielles)
En comparaison Ensuite, les méthodes de conception d'invites de format de code telles que Program of Thought (PoT) et PAL utilisent des outils externes (c'est-à-dire des interpréteurs Python) pour simplifier considérablement le processus de résolution mathématique. Cette approche consiste à confier le processus de calcul à un interpréteur Python externe pour résoudre des raisonnements mathématiques et algorithmiques complexes (comme la résolution d'équations quadratiques à l'aide de sympy ou le calcul des valeurs propres matricielles à l'aide de numpy). Cependant, PoT a du mal avec des scénarios de raisonnement plus abstraits, tels que le raisonnement de bon sens, la logique formelle et l'algèbre abstraite, en particulier sans API intégrée.
Afin de prendre en compte les avantages des méthodes CoT et PoT, l'équipe a introduit un nouvel ensemble de données de réglage fin des instructions mathématiques hybrides MathInstruct, qui présente deux caractéristiques principales : (1) couvrant largement différents domaines mathématiques et diplômes complexes , (2) Fusion des principes CoT et PoT
MathInstruct est basé sur sept ensembles de données de principes mathématiques existants et six ensembles de données nouvellement compilés. Ils ont utilisé MathInstruct pour affiner les modèles de lamas de différentes tailles (de 7B à 70B). Ils ont appelé le modèle résultant le modèle MAmmoTH et ont découvert que MAmmoTH avait des capacités sans précédent, à la manière d'un généraliste mathématique.
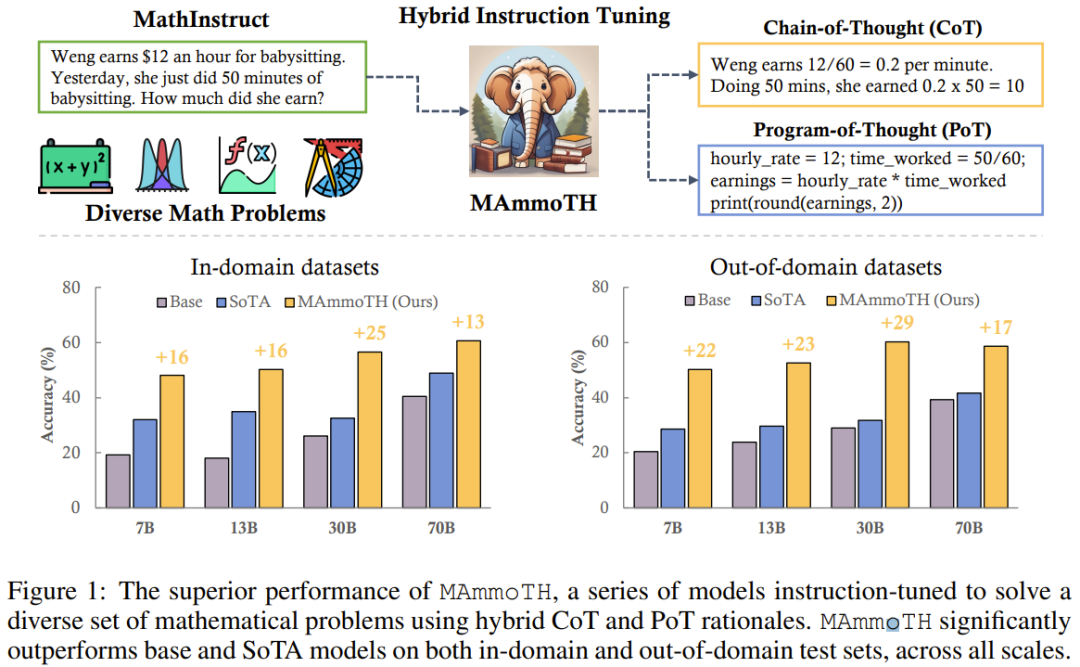
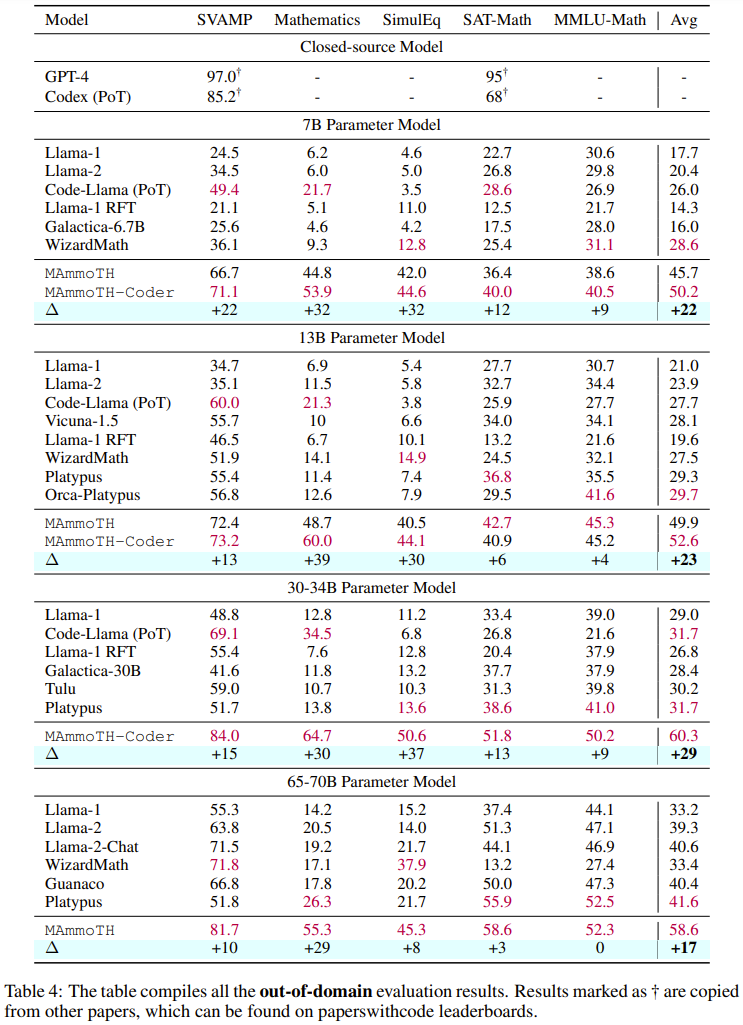
Pour évaluer MAmmoTH, l'équipe de recherche a utilisé une série d'ensembles de données d'évaluation, y compris des ensembles de tests au sein du domaine (GSM8K, MATH, AQuA-RAT, NumGLUE) et des ensembles de tests en dehors du domaine (SVAMP, SAT, MMLU-Math, Mathematics, SimulEq)
Les résultats de recherche montrent que le modèle MAmmoTH est plus performant en matière de généralisation à des ensembles de données hors domaine et améliore également considérablement la capacité du LLM open source en raisonnement mathématique
Il convient de noter que sur l'ensemble de données MATH de niveau compétition couramment utilisé, la version 7B de MAmmoTH a réussi à vaincre WizardMath (qui était le meilleur modèle open source précédent sur MATH) de 3,5 fois (35,2 % contre 10,7 %), et après ajustement fin, le 34B MAmmoTH-Coder peut même dépasser GPT-4 en utilisant CoT
La contribution de cette recherche peut être résumée en deux aspects : (1) En termes d'ingénierie des données, ils ont proposé un enseignement mathématique de haute qualité ensemble de données de réglage fin, qui contient une variété de problèmes mathématiques et de principes de mélange différents. (2) En termes de modélisation, ils ont formé et évalué plus de 50 nouveaux modèles différents et modèles de base allant de 7B à 70B pour explorer l'impact de différentes sources de données et formats d'entrée-sortie
Les résultats de la recherche montrent que , Les nouveaux modèles tels que MAmmoTH et MAmmoTH-Coder surpassent considérablement les modèles open source précédents en termes de précision

- Papier : https://arxiv.org/pdf/2309.05653.pdf
- Code : https://github.com/TIGER-AI-Lab/MAmmoTH
- Ensemble de données avec le modèle : https://huggingface.co/datasets/TIGER-Lab/MathInstruct
L'équipe a publié l'ensemble de données qu'elle a compilé et a ouvert le code de la nouvelle méthode et l'a publié sur Hugging Face au En même temps, l'équipe vise à compiler une liste d'un ensemble de données de réglage fin de l'enseignement mathématique de haute qualité et diversifiées qui devrait avoir deux caractéristiques principales : (1) couvrir largement différents domaines mathématiques et niveaux de complexité, et (2) combiner les principes CoT et PoT.
Pour la première fonctionnalité, les chercheurs ont d'abord sélectionné des ensembles de données de haute qualité largement utilisés couvrant différents domaines mathématiques et niveaux de complexité, tels que GSM8K, MATH, AQuA, Camel et TheoremQA. Ils ont ensuite remarqué un manque de mathématiques de niveau collégial, comme l’algèbre abstraite et la logique formelle, dans les ensembles de données existants. Pour résoudre ce problème, ils ont utilisé un petit nombre d'exemples de départ trouvés en ligne, ont synthétisé le principe CoT de la question dans TheoremQA en utilisant GPT-4 et ont créé un appariement « question-CoT » de manière autoguidée
Pour la deuxième fonctionnalité, combinant les principes CoT et PoT, peut améliorer la polyvalence de l'ensemble de données, rendant les modèles qu'il entraîne capables de résoudre différents types de problèmes mathématiques. Cependant, la plupart des ensembles de données existants fournissent des justifications procédurales limitées, ce qui entraîne un déséquilibre entre les principes CoT et PoT. À cette fin, l’équipe a utilisé GPT-4 pour compléter les principes PoT pour des ensembles de données sélectionnés, notamment MATH, AQuA, GSM8K et TheoremQA. Ces programmes synthétisés GPT-4 sont ensuite filtrés en comparant leurs résultats d'exécution avec la vérité terrain annotée par l'homme, garantissant ainsi que seuls des principes de haute qualité sont ajoutés.
Suite à ces directives, ils ont créé un nouvel ensemble de données MathInstruct, comme détaillé dans le tableau 1 ci-dessous.
Il contient 260 000 paires (instructions, réponses), couvrant un large éventail de domaines mathématiques de base (arithmétique, algèbre, probabilités, calcul et géométrie, etc.), y compris les principes mixtes CoT et PoT, et a différents langue et difficulté.
Réinitialiser la formation
Tous les sous-ensembles de MathInstruct sont unifiés dans une structure similaire à l'ensemble de données d'instruction d'Alpaca. Cette opération de normalisation garantit que le modèle affiné résultant peut gérer les données de manière cohérente, quel que soit le format de l'ensemble de données d'origine 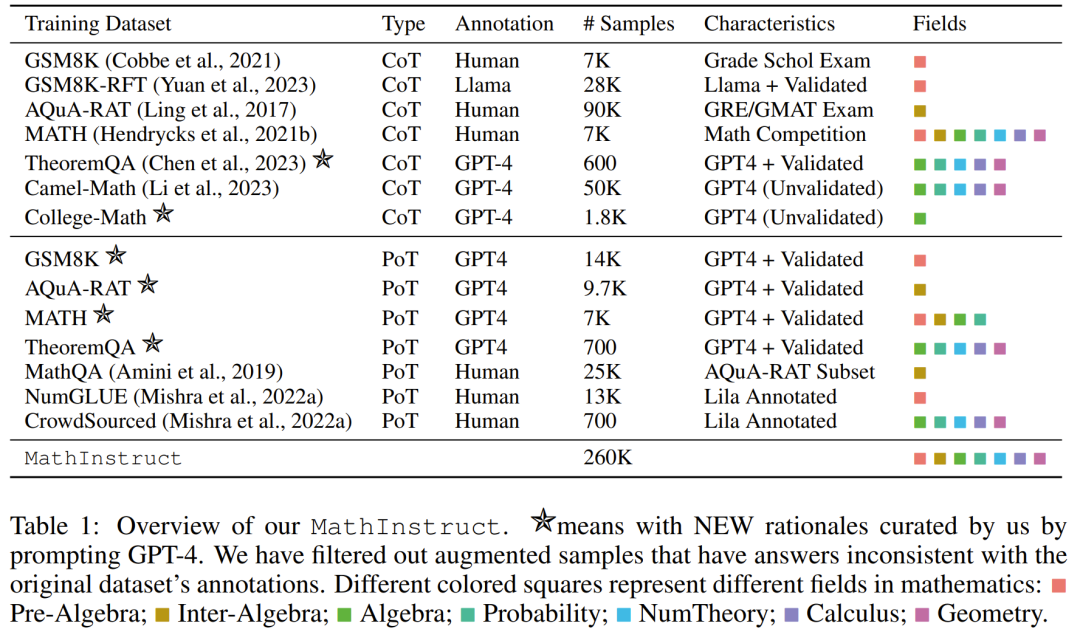
Pour le modèle de base, l'équipe a choisi Llama-2 et Code Llama
via MathInstruct Pour les ajustements, ils ont obtenu des modèles de différentes tailles, dont 7B, 13B, 34B et 70B. ensemble, voir le tableau 2 ci-dessous, contient de nombreux échantillons différents sur le terrain et hors terrain, couvrant plusieurs domaines différents des mathématiques.
L'ensemble de données d'évaluation contient différents niveaux de difficulté, notamment les niveaux primaire, secondaire et universitaire. Certains ensembles de données incluent également une logique formelle et un raisonnement de bon sens
Les ensembles de données d'évaluation sélectionnés comportent à la fois des questions ouvertes et des questions à choix multiples.
Pour les problèmes ouverts (tels que GSM8K et MATH), les chercheurs ont adopté le décodage PoT car la plupart de ces problèmes peuvent être résolus par programme. ,
Pour les questions à choix multiples (telles que AQuA et MMLU), les chercheurs ont adopté le décodage CoT car la plupart des questions de cet ensemble de données peuvent être mieux traitées par CoT. Le décodage CoT ne nécessite aucun mot déclencheur, tandis que le décodage PoT nécessite un mot déclencheur : "Écrivons un programme pour résoudre le problème".
Principaux résultats
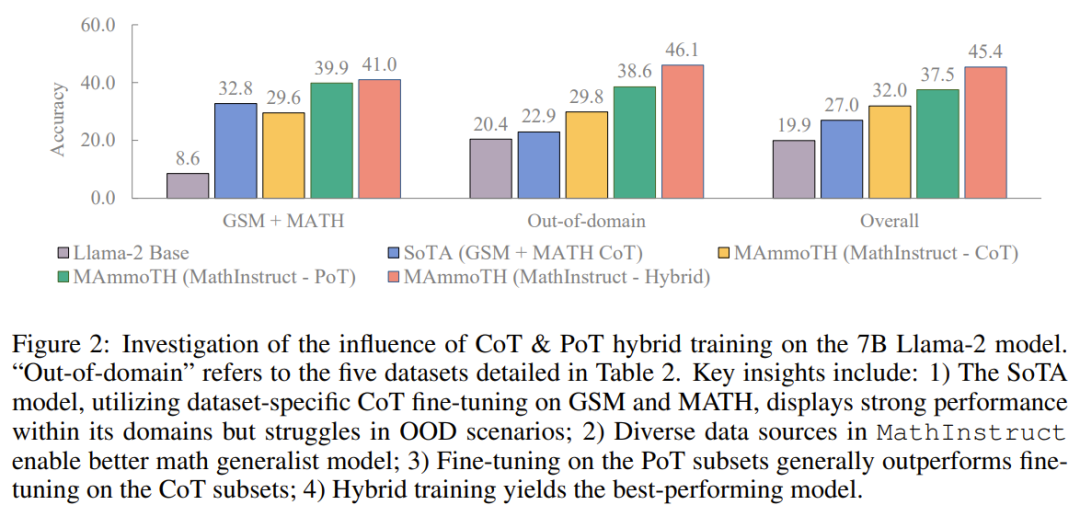
Dans l'ensemble, MAmmoTH et MAmmoTH-Coder surpassent les meilleurs modèles précédents dans différentes tailles de modèle. Le nouveau modèle permet d'obtenir davantage de gains de performances sur les ensembles de données hors domaine que sur les ensembles de données intra-domaine. Ces résultats indiquent que le nouveau modèle a le potentiel de devenir un généraliste mathématique. MAmmoTH-Coder-34B et MAmmoTH-70B surpassent même le LLM à source fermée sur certains ensembles de données. Les chercheurs ont également comparé en utilisant différents modèles de base. Plus précisément, ils ont mené des expériences comparant deux modèles de base, Llama-2 et Code-Llama. Comme le montrent les deux tableaux ci-dessus, Code-Llama est globalement meilleur que Llama-2, en particulier sur les ensembles de données hors champ. L'écart entre MAmmoTH et MAmmoTH-Coder peut même atteindre 5% Exploration de la recherche sur l'ablation sur les sources de données Ils ont mené des recherches pour explorer la source des gains de performances. Afin de mieux comprendre la source des avantages de MAmmoTH par rapport aux modèles de référence existants, les chercheurs ont mené une série d'expériences contrôlées. Les résultats sont présentés dans la figure 2. En résumé, les avantages significatifs en termes de performances de MAmmoTH peuvent être attribués à : 1) Diverses sources de données couvrant. différents domaines mathématiques et niveaux de complexité, 2) Stratégies hybrides pour le réglage fin des instructions CoT et PoT.
D'après les résultats du tableau 5, on constate que si la diversité de l'ensemble de données d'entraînement est insuffisante (par exemple, lorsqu'il n'y a que GSM8K), la capacité de généralisation du modèle est très mauvais : le modèle ne peut s'adapter qu'à des situations au sein de la distribution des données, il est difficile de résoudre des problèmes au-delà des problèmes GSM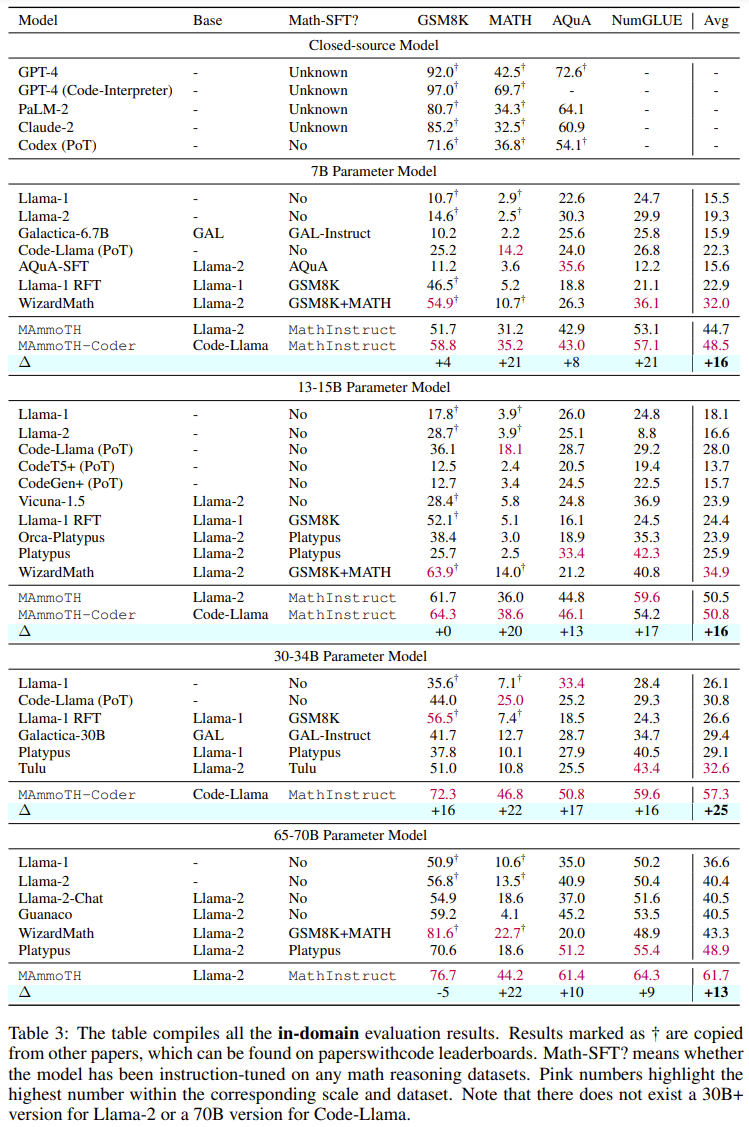
 Ils ont également étudié l'impact des principaux sous-ensembles. En ce qui concerne les diverses sources de MathInstruct utilisées pour entraîner MAmmoTH, il est également important de comprendre dans quelle mesure chaque source contribue aux performances globales du modèle. Ils se concentrent sur quatre sous-ensembles principaux : GSM8K, MATH, Camel et AQuA. Ils ont mené une expérience dans laquelle chaque ensemble de données a été progressivement ajouté à la formation et ont comparé les performances à un modèle affiné sur l'ensemble de MathInstruct.
Ils ont également étudié l'impact des principaux sous-ensembles. En ce qui concerne les diverses sources de MathInstruct utilisées pour entraîner MAmmoTH, il est également important de comprendre dans quelle mesure chaque source contribue aux performances globales du modèle. Ils se concentrent sur quatre sous-ensembles principaux : GSM8K, MATH, Camel et AQuA. Ils ont mené une expérience dans laquelle chaque ensemble de données a été progressivement ajouté à la formation et ont comparé les performances à un modèle affiné sur l'ensemble de MathInstruct. 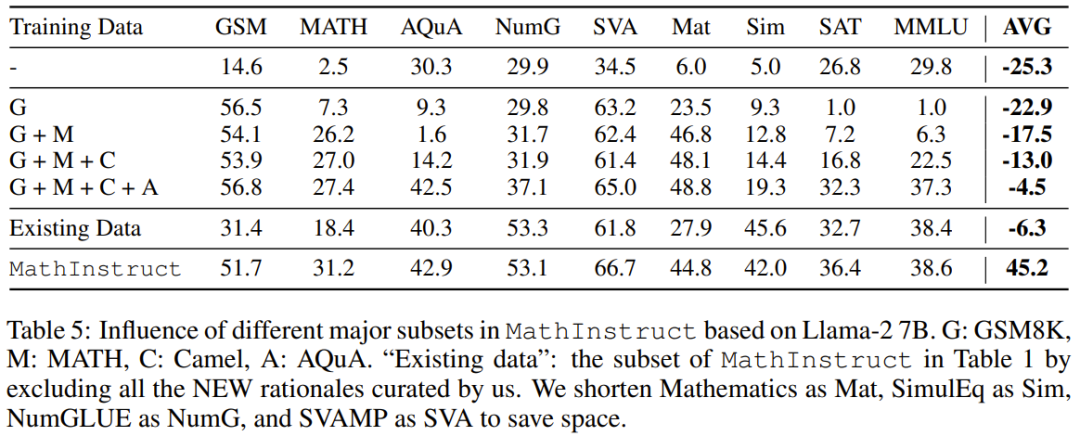 L'impact important de diverses sources de données sur MAmmoTH est mis en évidence dans ces résultats, qui sont également la clé fondamentale de faisant de MAmmoTH un généraliste mathématique. Ces résultats fournissent également des informations et des conseils précieux pour nos futurs efforts de conservation et de collecte de données. Par exemple, nous devrions toujours collecter des données diverses et éviter de collecter uniquement des types de données spécifiques
L'impact important de diverses sources de données sur MAmmoTH est mis en évidence dans ces résultats, qui sont également la clé fondamentale de faisant de MAmmoTH un généraliste mathématique. Ces résultats fournissent également des informations et des conseils précieux pour nos futurs efforts de conservation et de collecte de données. Par exemple, nous devrions toujours collecter des données diverses et éviter de collecter uniquement des types de données spécifiques
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Quels sont les modèles de données couramment utilisés ?
- Quels sont les trois types de modèles de données de base de données ?
- Quels sont les trois modèles de données de base de données courants ?
- Comment supprimer des modèles redondants dans ZBrush
- Quel est le modèle de couleur utilisé par les écrans d'ordinateur ?

