Étant donné un graphe acyclique, calculez la somme minimale des éléments à chaque profondeur

Un graphe qui ne contient aucun cycle ni boucle est appelé graphe acyclique. Un arbre est un graphe acyclique dans lequel chaque nœud est connecté à un autre nœud unique. Les graphiques acycliques sont également appelés graphiques acycliques.

La différence entre les graphiques cycliques et acycliques -

La traduction chinoise de est :

Cycle Graph	Cycle Graph	Graphique acyclique
Le graphique forme une boucle fermée.	Le graphique ne forme pas une boucle fermée.
Les boucles profondes ne sont pas incluses dans le graphique	Les graphiques contiennent toutes les profondeurs.

Exemple 1

Prenons un exemple de graphique cyclique −

Lorsqu'une boucle fermée existe, un graphe cyclique est formé.

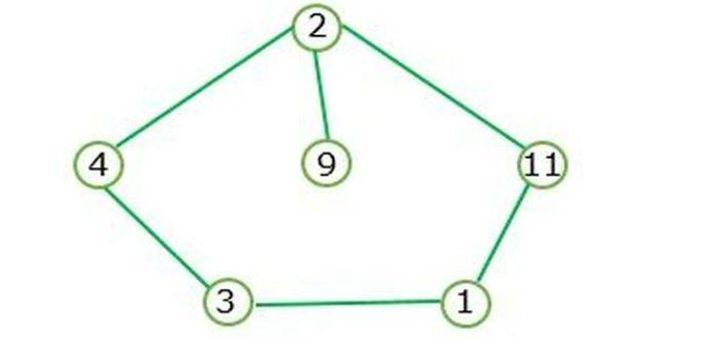
La figure I représente le graphique du cycle et ne contient pas de nœuds de profondeur.

Exemple 2

se traduit par :

Exemple 2

Illustrons avec un exemple de graphe acyclique :

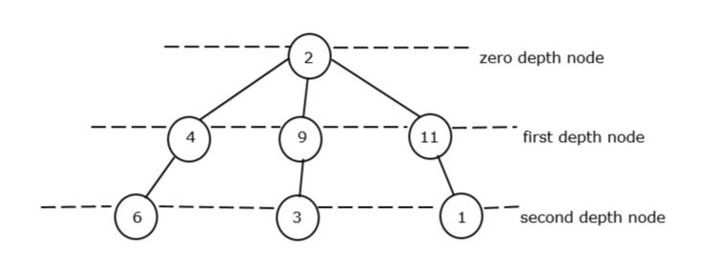
Le nœud racine de l’arbre est appelé nœud de profondeur nulle. Dans la figure II, il n’y a qu’une seule racine à profondeur nulle, soit 2. Il est donc considéré comme un nœud de profondeur minimale nulle.

Dans le premier nœud de profondeur, nous avons 3 éléments de nœud comme 4, 9 et 1, mais le plus petit élément est 4.

Dans le deuxième nœud de profondeur, nous avons à nouveau 3 éléments de nœud comme 6, 3 et 1 mais l'élément minimum est 1.

Nous saurons comment le nœud de profondeur totale est dérivé,

Nœud de profondeur totale = valeur minimale du nœud Zero_Depth + valeur minimale du nœud First_Depth + valeur minimale du nœud Zero_Depth

Profondeur totale des nœuds = 2 + 4 + 3 = 9. Ainsi, 9 est la somme minimale totale du graphe acyclique.

Grammaire

The following syntax used in the program:
struct name_of_structure{
   data_type var_name;   
   // data member or field of the structure.
}

• struct - Ce mot-clé est utilisé pour représenter le type de données de structure.

• name_of_struct - Nous fournissons n'importe quel nom pour la structure.

• Une structure est un ensemble de diverses variables liées en un seul endroit.

Queue < pair < datatype, datatype> > queue_of_pair

make_pair() 

Paramètres

File d'attente de paires en C++ -

• Il s'agit d'un modèle STL générique permettant de combiner des paires de files d'attente de deux types de données différents, les paires de files d'attente sont situées sous le fichier d'en-tête de l'utilitaire.

• Queue_of_pair - Nous donnons à la paire n'importe quel nom.

• make_pair() - Utilisé pour construire un objet paire avec deux éléments.

name_of_queue.push()

Paramètres

• name_of_queue - Nous nommons le nom de la file d'attente.

• push() - Il s'agit d'une méthode prédéfinie qui fait partie de la tête de file d'attente. La méthode push est utilisée pour insérer des éléments ou des valeurs.

name_of_queue.pop()

Paramètres

• name_of_queue − Nous donnons un nom à la file d'attente.

• pop() - Il s'agit d'une méthode prédéfinie qui appartient au fichier d'en-tête de file d'attente, et la méthode pop est utilisée pour supprimer l'intégralité de l'élément ou de la valeur.

Algorithme

• Nous allons démarrer les fichiers d'en-tête du programme, à savoir 'iostream', 'climits', 'utility', et 'queue'.

• Nous créons une structure "tree_node" avec une valeur entière "val" pour obtenir la valeur du nœud. Nous créons ensuite un tree_node pointeur avec les données fournies pour initialiser les nœuds enfants gauche et droit pour stocker les valeurs. Ensuite, nous créons une fonction tree_node où int x est passé comme argument et vérifions qu'il est égal à un entier 'val' et attribuons les nœuds enfants gauche et droit à null .

• Maintenant, nous allons définir une fonction minimum_sum_at_each_degree() qui accepte une valeur entière comme argument pour trouver la somme minimale à chaque profondeur. À l'aide d'une instruction if-, il vérifie si la valeur racine de l'arborescence est vide et renvoie 0 si elle est vide.

• Nous créons des paires de files d'attente de STL (Standard Template Library) pour combiner deux valeurs.

• Nous créons une variable de file d'attente appelée q qui prend deux méthodes par paire, à savoir push() et make_pair(). En utilisant ces deux méthodes, nous insérons des valeurs et construisons deux paires d'un objet.

• Nous initialisons trois variables, à savoir 'present_degree', 'present_sum' et 'totalSum' qui seront utilisées pour trouver davantage la somme actuelle ainsi que pour trouver la somme minimale totale.

• Après avoir initialisé les variables, nous créons une boucle while pour vérifier la condition, si la paire de files d'attente n'est pas vide, le décompte des nœuds recommencera depuis le début. Ensuite, nous utilisons la méthode ‘pop()’ pour supprimer un nœud existant car il sera déplacé vers la profondeur suivante de l’arborescence pour calculer la somme minimale.

• Maintenant, nous allons créer trois instructions if pour renvoyer la somme minimale des sommes.

• Après cela, nous allons démarrer la fonction principale et construire la structure arborescente du mode de saisie à l'aide du pointeur racine, des sous-nœuds gauche et droit respectivement, et transmettre la valeur du nœud via le nouveau 'tree_node'.

• Enfin, nous appelons la fonction 'minimum_sum_at_each_degree(root)' et passons le paramètre root pour calculer la somme minimale à chaque profondeur. Ensuite, imprimez l'instruction "somme de chaque profondeur du graphe acyclique" et obtenez le résultat.

N'oubliez pas qu'une file d'attente par paire est un conteneur contenant des paires d'éléments de file d'attente.

La traduction chinoise de

Exemple

est :

Exemple

Dans ce programme, nous calculerons la somme de tous les nœuds minimaux pour chaque profondeur.

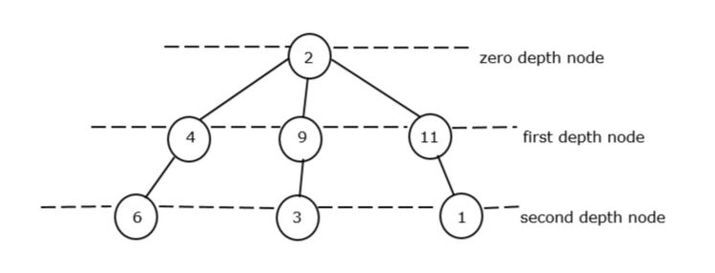
Dans la figure 2, la somme minimale de la profondeur totale est de 15+8+4+1 = 13.

现在我们将把这个数字作为该程序的输入。

#include <iostream>
#include <queue> 

// required for FIFO operation
#include <utility> 

// required for queue pair
#include <climits>
using namespace std;

// create the structure definition for a binary tree node of non-cycle graph
struct tree_node {
   int val;
   tree_node *left;
   tree_node *right;
   tree_node(int x) {
      val = x;
      left = NULL;
      right = NULL;
   }
};
// This function is used to find the minimum sum at each depth
int minimum_sum_at_each_depth(tree_node* root) {
   if (root == NULL) {
      return 0;
   }
   queue<pair<tree_node*, int>> q;
   // create a queue to store node and depth and include pair to combine two together values.
   q.push(make_pair(root, 0)); 
   
   // construct a pair object with two element
   int present_depth = -1; 
   
   // present depth
   int present_sum = 0; 
   
   // present sum for present depth
   int totalSum = 0; 
   
   // Total sum for all depths
   while (!q.empty()) {
      pair<tree_node*, int> present = q.front(); 
      
      // assign queue pair - present
      q.pop();
      
      // delete an existing element from the beginning
      if (present.second != present_depth) {
      
         // We are moving to a new depth, so update the total sum and reset the present sum
         present_depth = present.second;
         totalSum += present_sum;
         present_sum = INT_MAX;
      }

      // Update the present sum with the value of the present node
      present_sum = min(present_sum, present.first->val);
      
      //We are adding left and right children to the queue for updating the new depth.
      if (present.first->left) {
         q.push(make_pair(present.first->left, present.second + 1));
      }
      if (present.first->right) {
         q.push(make_pair(present.first->right, present.second + 1));
      }
   }
   
   // We are adding the present sum of last depth to the total sum
   totalSum += present_sum;
   return totalSum;
}

// start the main function
int main() {
   tree_node *root = new tree_node(15);
   root->left = new tree_node(14);
   root->left->left = new tree_node(11);
   root->left->right = new tree_node(4);
   root->right = new tree_node(8);
   root->right->left = new tree_node(13);
   root->right->right = new tree_node(16);
   root->left->left->left = new tree_node(1);
   root->left->right->left = new tree_node(6);
   root->right->right->right = new tree_node(2);
   root->right->left->right = new tree_node(7);

   cout << "Total sum at each depth of non cycle graph: " << minimum_sum_at_each_depth(root) << endl; 
   return 0;
}

输出

Total sum at each depth of non cycle graph: 28

结论

我们探讨了给定非循环图中每个深度的元素最小和的概念。我们看到箭头运算符连接节点并构建树形结构，利用它计算每个深度的最小和。该应用程序使用非循环图，例如城市规划、网络拓扑、谷歌地图等。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!