En C, le plus grand triangle de Reuleaux à l'intérieur d'un carré

Un Triangle de Lule est une forme formée par l'intersection de trois disques, le centre de chaque disque étant à la limite des deux autres disques. Sa limite est une courbe de largeur constante et, mis à part le cercle lui-même, c'est la courbe de ce type la plus simple et la plus connue. Une largeur constante signifie que l'espacement entre chacune des deux lignes de support parallèles est le même, quelle que soit leur orientation. Parce que tous ses diamètres sont les mêmes.

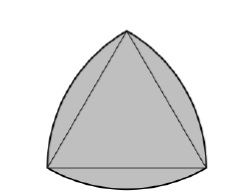
La limite du triangle de Lule est une courbe de largeur constante basée sur un triangle équilatéral. Tous les points d'une arête sont équidistants du sommet opposé.

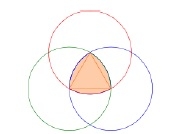
Construisez un triangle de Lule

La formule du triangle de Lule

Si la courbe est basée sur un triangle équilatéral et que la longueur du côté du triangle est h, alors l'aire du triangle de Lule est

A = (&pi; * h<sup>2</sup>) / 2 &ndash; 2 * (Area of equilateral triangle) = (&pi; &ndash; &radic;3) * h<sup>2</sup> / 2 = 0.70477 * h<sup>2</sup>

Trouvez le maximum à l'intérieur d'un carré du Triangle de Reuleaux

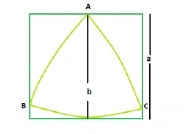
Prenons un exemple,

Input: a = 6
Output: 25.3717

illustre que l'aire du

Triangle de Reuleaux est 0.70477 * b², où b est la distance entre droites parallèles supportant le triangle de Reuleaux.

La distance entre les droites parallèles supportant le triangle de Reuleaux = la longueur du côté du carré, qui est a

L'aire du triangle de Reuleaux, A = 0,70477 * a²

Exemple

#include <stdio.h>
#include <math.h>
int main() {
   float a = 6;
   float area = 0.70477 * pow(a, 2);
   printf("The area is : %f",area);
   return 0;
}

sortie

The area is : 25.371719

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!