Programme C++ pour trouver le composant de score maximum qui peut être réduit à partir d'un graphique

Supposons qu'il existe un graphe non orienté pondéré avec n sommets et m arêtes. Le score d'un graphique est défini comme la somme des poids de toutes les arêtes du graphique. Les poids des bords peuvent être négatifs et s’ils sont supprimés, le score du graphique augmentera. Ce que nous devons faire est de minimiser le score du graphique en supprimant les arêtes du graphique tout en conservant la connectivité du graphique. Nous devons trouver le score maximum qui peut être réduit.

Le graphique est donné sous la forme d'un tableau 'edges', où chaque élément est de la forme {weight, {vertex1, vertex2}}.

Donc, si l'entrée est n = 5, m = 6, bords = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3 , {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}, alors la sortie sera 4.

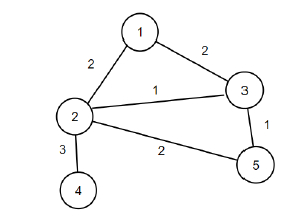
Si nous supprimons les arêtes (1, 2) et (2, 5) du graphique, la réduction totale du score sera de 4 et le graphique restera toujours connecté.

Pour résoudre ce problème, nous suivrons les étapes suivantes :

cnum := 0
Define an array par of size: 100.
Define an array dim of size: 100.
Define a function make(), this will take v,
   par[v] := v
   dim[v] := 1
Define a function find(), this will take v,
   if par[v] is same as v, then:
      return v
   return par[v] = find(par[v])
Define a function unify(), this will take a, b,
a := find(a)
b := find(b)
if a is not equal to b, then:
   (decrease cnum by 1)
   if dim[a] > dim[b], then:
      swap values of (a, b)
   par[a] := b
   dim[b] := dim[b] + dim[a]
cnum := n
sort the array edges based on edge weights
for initialize i := 1, when i <= n, update (increase i by 1), do:
   make(i)
res := 0
for each edge in edges, do:
   a := first vertex of edge
   b := second vertex of edge
   weight := weight of edge
   if find(a) is same as find(b), then:
      if weight >= 0, then:
         res := res + 1 * weight
      Ignore following part, skip to the next iteration
   if cnum is same as 1, then:
      if weight >= 0, then:
         res := res + 1 * weight
   Otherwise
      unify(a, b)
return res

Exemple

Voyons l'implémentation suivante pour une meilleure compréhension -

#include <bits/stdc++.h>
using namespace std;

int cnum = 0;
int par[100];
int dim[100];

void make(int v){
   par[v] = v;
   dim[v] = 1;
}
int find(int v){
   if(par[v] == v)
   return v;
   return par[v] = find(par[v]);
}
void unify(int a, int b){
   a = find(a); b = find(b);
   if(a != b){
      cnum--; if(dim[a] > dim[b]){
         swap(a, b);
      }
      par[a] = b; dim[b] += dim[a];
   }
}
int solve(int n, int m, vector <pair <int, pair<int,int>>> edges){
   cnum = n;
   sort(edges.begin(), edges.end());
   for(int i = 1; i <= n; i++)
      make(i);
   int res = 0;
   for(auto &edge : edges){
      int a = edge.second.first;
      int b = edge.second.second;
      int weight = edge.first;
      if(find(a) == find(b)) {
         if(weight >= 0) 
            res += 1 * weight;
         continue;
      }
      if(cnum == 1){
         if(weight >= 0)
            res += 1 * weight;
      } else{
         unify(a, b);
      }
   }
   return res;
}
int main() {
   int n = 5, m = 6;
   vector <pair<int, pair<int,int>>> edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}};
   cout<< solve(n, m, edges);
   return 0;
}

Input

5, 6, {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}

Output

4

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!