Qu’est-ce qu’un arbre AA en C/C++ ?

En informatique, un arbre AA est défini comme une implémentation d'arbre équilibrée pour un stockage et une récupération efficaces des données ordonnées. Les arbres AA sont considérés comme une variante des arbres rouge-noir, un arbre de recherche binaire qui prend en charge l'ajout et la suppression efficaces d'entrées. Contrairement à l'arborescence rouge-noir, le nœud rouge de l'arborescence AA ne peut être ajouté qu'en tant que nœud enfant droit et ne peut pas être ajouté en tant que nœud enfant gauche. Le résultat de cette opération est de simuler un arbre 2-3 au lieu d'un arbre 2-3-4, simplifiant ainsi les opérations de maintenance. L'algorithme de maintenance des arbres rouge-noir doit prendre ou considérer sept formes différentes pour équilibrer correctement l'arbre.

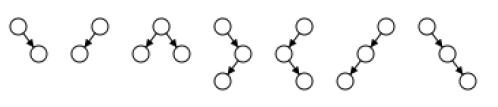
Contrairement aux arbres rouge-noir, les arbres AA n'ont besoin que d'assumer ou de considérer deux formes puisque seul le bon lien peut être rouge.

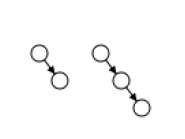
Rotation équilibrée

L'arbre rouge-noir nécessite un bit de métadonnées d'équilibrage (couleur) par nœud, tandis que l'arbre AA nécessite des bits de métadonnées O(log(log(N))) par nœud, sous la forme d'un "niveau" entier. L'invariant suivant s'applique aux arbres AA :

• Le niveau de chaque nœud feuille est considéré comme étant 1.

• Le niveau de chaque nœud enfant gauche est inférieur de 1 à celui de son nœud parent.

• Le niveau de chaque nœud enfant droit est égal ou inférieur de 1 à celui de son nœud parent.

• Le niveau de chaque nœud petit-enfant droit est strictement plus petit que son nœud grand-parent.

• Chaque nœud de niveau supérieur à 1 a deux nœuds enfants.

Rééquilibrer un arbre AA est bien plus simple que rééquilibrer un arbre rouge-noir.

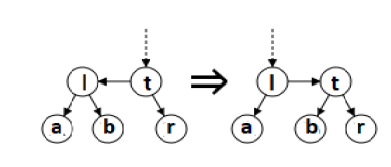
Dans un arbre AA, seules deux opérations différentes sont nécessaires pour rétablir l'équilibre : « skew » et « split ». L'inclinaison est traitée comme une rotation à droite, remplaçant un sous-arbre constitué d'un lien horizontal gauche par un lien horizontal droit. Dans le cas de Split, il tourne à gauche et augmente de niveau, remplaçant un sous-arbre contenant deux liens horizontaux droits moins consécutifs par deux liens horizontaux droits consécutifs ou plus. Les deux opérations « skew » et « split » sont expliquées ci-dessous. La définition de

function skew est la suivante :

   input: An AA tree that needs to be rebalanced is represented by a node, t.
   output: The rebalanced AA tree is represented by another node.
if nil(t) then
return nil
else if nil(left(t)) then
return t
else if level(left(t)) == level(t) then
   Exchange the pointers of horizontal left links.
   l = left(t)
left(t) := right(l)
right(l) := t
return l
else
return t
end if
end function

la fonction split est

La traduction est :

la fonction split est

   input: An AA tree that needs to be rebalanced is represented by a node, t.
   output: The rebalanced AA tree is represented by another node.
if nil(t) then
return nil
else if nil(right(t)) or nil(right(right(t))) then
return t
else if level(t) == level(right(right(t))) then
We have two horizontal right links. The middle node is taken, elevate it, and return it.
      r = right(t)
right(t) := left(r)
left(r) := t
level(r) := level(r) + 1
return r
else
return t
end if
end function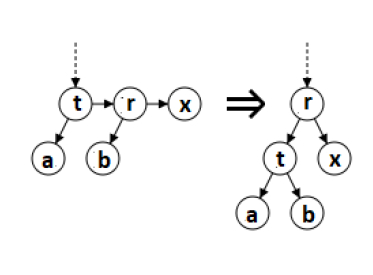

Partager -

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!