Visualisez O(n) en utilisant Python.

Présentation

Dans le domaine de l'informatique et de la programmation, comprendre l'efficacité des algorithmes est crucial car cela aide à créer des logiciels à la fois optimisés et performants. La complexité temporelle est un concept important dans ce contexte car elle mesure la façon dont le temps d'exécution d'un algorithme change à mesure que la taille de l'entrée augmente. La classe de complexité temporelle O(n) couramment utilisée représente une relation linéaire entre la taille d'entrée et le temps d'exécution.

Définition

La complexité des algorithmes en informatique est l'évaluation des ressources requises, telles que l'utilisation du temps et de l'espace, en fonction de la taille d'entrée d'un algorithme. De plus, cela conforte notre compréhension de la rapidité d’exécution d’un algorithme lorsque la taille de son entrée est prise en compte. La principale notation utilisée pour décrire la complexité d'un algorithme est la notation Big O (O(n)).

Grammaire

for i in range(n):
   # do something

Une boucle `for` qui exécute un ensemble spécifique d'instructions basé sur une plage de 0 à `n-1` et effectue une opération ou un ensemble d'opérations à chaque itération. où « n » représente le nombre d'itérations.

Sous complexité temporelle O(n), à mesure que la taille d'entrée « n » augmente, le temps d'exécution augmente proportionnellement. À mesure que « n » augmente, le nombre d’itérations de la boucle et le temps nécessaire pour terminer la boucle augmenteront proportionnellement. La complexité temporelle linéaire présente une relation proportionnelle directe entre la taille de l'entrée et le temps d'exécution.

Toute tâche ou séquence de tâches peut être exécutée en boucle quelle que soit la taille d'entrée 'n'. Le principal aspect à noter ici est que la boucle exécute « n » itérations, ce qui entraîne une complexité temporelle linéaire.

Algorithme

• Étape 1 : Initialiser une somme variable à 0

• Étape 2 : Parcourez chaque élément de la liste fournie

• Étape 3 : Fusionnez l'élément dans la valeur de somme actuelle.

• Étape 4 : La somme doit être restituée une fois la boucle terminée.

• Étape 5 : Fin

Méthode

• Méthode 1 : Relation entre le temps de dessin et la taille d'entrée

• Méthode 2 : La relation entre les opérations de dessin et l'échelle d'entrée

Méthode 1 : Temps de tracé en fonction de la taille d'entrée

Exemple

import time
import matplotlib.pyplot as plt

def algo_time(n):
    sum = 0
    for i in range(n):
        sum += i
    return sum

input_sizes = []
execution_times = []

for i in range(1000, 11000, 1000):
    start_time = time.time()
    algo_time(i)
    end_time = time.time()
    input_sizes.append(i)
    execution_times.append(end_time - start_time)

plt.plot(input_sizes, execution_times)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (s)')
plt.show()

Sortie

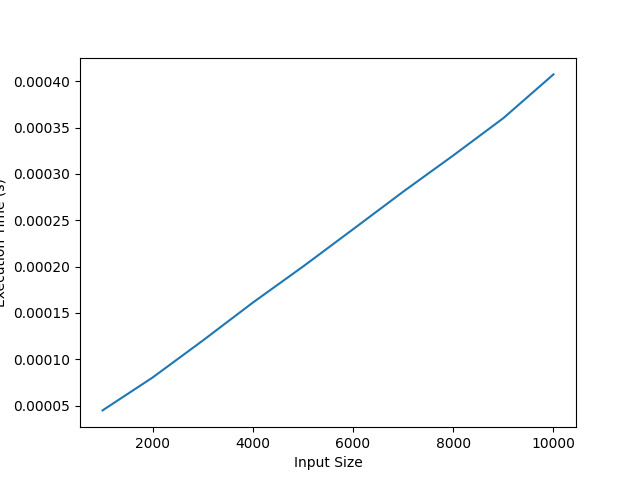
Ce code est utilisé pour mesurer le temps d'exécution de l'algorithme `algo_time()` sous différentes tailles d'entrée. Nous stockerons les tailles d'entrée que nous souhaitons tester et leurs temps d'exécution correspondants dans ces listes.

Utilisez une boucle « pour » pour parcourir une plage de tailles d'entrée. Dans ce cas, la boucle s'étendra de 1 000 jusqu'à plus près de 11 000, en incrémentant de 1 000 à chaque fois. Pour illustrer davantage, nous prévoyons d'évaluer l'algorithme en faisant varier la valeur de « n » de 1 000 à 10 000 par incréments de 1 000.

À l'intérieur de la boucle, nous mesurons le temps d'exécution de la fonction `algo_time()` pour chaque taille d'entrée. Pour commencer à suivre le temps, nous utilisons `time.time()` avant d'appeler la fonction, et l'arrêtons dès que la fonction a fini de s'exécuter. Nous stockons ensuite la durée dans une variable appelée « execution_time ».

Nous ajoutons chaque valeur d'entrée d'une taille d'entrée donnée ("n") et son temps d'exécution correspondant à leurs listes respectives ("input_sizes" et "execution_times").

Une fois la boucle terminée, nous disposons des données dont nous avons besoin pour générer le tracé. 'plt.plot(input_sizes, exécution_times)' génère un graphique linéaire de base en utilisant les données que nous avons collectées. L'axe des X montre les valeurs « input_sizes » représentant différentes tailles d'entrée.

'plt.xlabel()' et 'plt.ylabel()' sont enfin utilisés pour marquer respectivement la signification des axes de coordonnées, et appeler la fonction 'plt.show()' nous permet de présenter le graphique.

En exécutant ce code, nous pouvons visualiser l'augmentation du temps d'exécution à mesure que la taille d'entrée (« n ») augmente en traçant un graphique. En supposant que la complexité temporelle de l'algorithme est O(n), nous pouvons approximer qu'il existe une corrélation presque linéaire entre la taille d'entrée et le temps d'exécution lors du traçage du graphique.

Méthode 2 : La relation entre l'opération de dessin et la taille d'entrée

Exemple

import matplotlib.pyplot as plt

def algo_ops(n):
    ops = 0
    sum = 0
    for i in range(n):
        sum += i
        ops += 1
    ops += 1  # for the return statement
    return ops

input_sizes = []
operations = []

for i in range(1000, 11000, 1000):
    input_sizes.append(i)
    operations.append(algo_ops(i))

plt.plot(input_sizes, operations)
plt.xlabel

plt.xlabel('Input Size')
plt.ylabel('Number of Operations')
plt.show()

Sortie

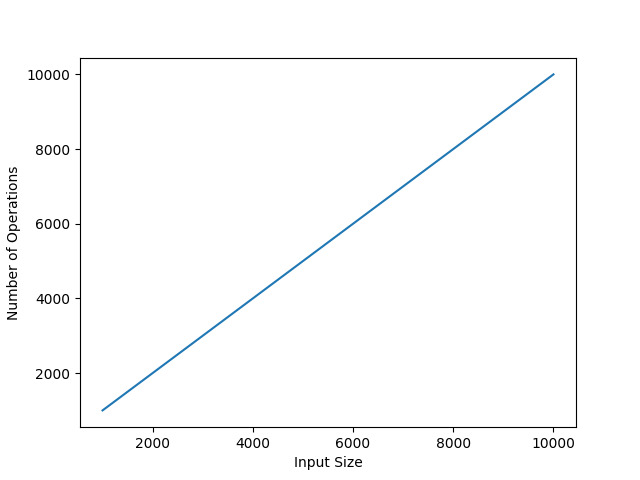
Ce code est conçu pour analyser le nombre d'opérations effectuées par l'algorithme `algo_ops()` sous différentes tailles d'entrée. En utilisant la fonction `algo_ops()`, vous pouvez calculer la somme de toutes les valeurs comprises entre zéro et l'argument d'entrée « n » donné, tout en suivant et en enregistrant simultanément chaque opération effectuée pendant chaque calcul.

Nous importons d'abord le module 'matplotlib.pyplot', qui nous permet de créer des visualisations telles que des graphiques.

Ensuite, nous définissons la fonction algo_ops(), qui accepte un nombre d'entrée 'n'. À l'intérieur de la fonction, nous initialisons deux variables : « ops » pour compter le nombre d'opérations et « sum » pour stocker la somme cumulée des nombres.

Ces tableaux stockeront les dimensions que nous souhaitons vérifier et leur durée d'exécution correspondante.

Une façon d'utiliser les boucles itératives consiste à effectuer une boucle sur plusieurs échelles d'entrée. Dans ce cas, la plage d'exécution de la boucle est de 1000 à 10000 (sauf 11000). Cela signifie que nous évaluerons la technique avec la variable « n » comprise entre 1 000 et 10 000 par incréments de 100.

Dans la boucle, nous calculons les performances du processus `algo_time()` pour toutes les tailles d'entrée. Nous utilisons `time.time()` pour démarrer un chronomètre avant d'appeler la procédure, et le terminer directement après la fin de l'exécution du sous-programme. Ensuite, nous enregistrons l'intervalle de temps dans une variable appelée « execution_period ».

Pour chaque taille d'entrée, nous incluons la valeur de l'entrée (« n ») dans une liste appelée « input_sizes ». De plus, nous ajoutons les temps de traitement correspondants dans la collection «execution_times».

Une fois la boucle terminée, nous avons accumulé les données de base nécessaires à la création du graphique. L'instruction « plt.plot(input_sizes, exécuté_times) » crée un graphique linéaire de base en utilisant les données collectées. Les valeurs de « input_sizes » sont affichées sur l'axe des x et représentent différentes tailles d'entrée. La valeur de 'execution_times' est affichée sur l'axe vertical et représente le temps requis pour exécuter la fonction `algo_time()` avec différentes tailles d'entrée.

Enfin, nous étiquetons le système de coordonnées via 'plt.xlabel()' et 'plt.ylabel()' pour montrer la signification de chaque axe. Ensuite, exécutez la fonction 'plt.show()' pour afficher le graphique.

Une fois le programme exécuté, le graphique nous montrera comment le temps de traitement augmente lorsque la taille de l'entrée (« n ») augmente.

Conclusion

En résumé, maîtriser la complexité temporelle et la visualisation en Python à l'aide de Matplotlib est une compétence précieuse pour tout programmeur cherchant à créer des solutions logicielles efficaces et optimisées. Comprendre comment les algorithmes se comportent à différentes échelles d'entrée nous permet de résoudre des problèmes complexes et de créer des applications robustes qui fournissent des résultats de manière rapide et efficace.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!