Vérifie si un graphique construit à partir d'un tableau basé sur une condition donnée contient un cycle

Présentation

En théorie des graphes, c'est une tâche très importante de déterminer si un graphe construit à partir de tableaux et satisfaisant certaines conditions a un cycle. Un diagramme est une manière imaginative de montrer comment les choses sont connectées. Il est utilisé dans de nombreux endroits, comme les réseaux informatiques et les réseaux sociaux. Cet article traite des conditions de construction de graphiques, des algorithmes BFS et DFS, et fournit des instructions étape par étape sur la façon d'identifier les cycles dans les graphiques non orientés.

Représentation matricielle du graphique

Les méthodes basées sur les tableaux dans la théorie des graphes stockent les sommets et les arêtes dans des tableaux, ce qui les rend faciles à utiliser et à utiliser dans les algorithmes. Commencer avec un graphique vide, ajouter des sommets et des arêtes un par un en fonction des informations contenues dans le tableau constitue la base d'une exploration plus approfondie, telle que la détection de cycles, ce qui est important pour comprendre comment le graphique est lié et s'il existe des cycles.

Conditions de construction du graphique

Explication des conditions données

• Les graphiques sont construits à partir de tableaux, où les tableaux représentent un ensemble de sommets et leurs connexions ou arêtes.

• Chaque élément du tableau correspond à un sommet dans le graphique

• La valeur de chaque élément du tableau représente l'index du sommet auquel il est connecté (ses sommets voisins).

• L'index du tableau représente le sommet lui-même et sa valeur correspondante représente le sommet auquel il est connecté.

Conditions de vérification de la construction d'un graphe

• Vérifiez si le tableau est valide et répond aux conditions requises avant de construire le graphique.

• Assurez-vous que le tableau n'est pas vide et contient au moins un élément pour créer le sommet.

• Vérifiez que le tableau ne contient que des entiers non négatifs, car les valeurs négatives ou les données invalides ne peuvent pas représenter des sommets ou des arêtes valides

• Assurez-vous que l'index du tableau se situe dans la plage appropriée. Ils doivent commencer à 0 et aller à n-1, où n est le nombre total de sommets du graphique.

• Confirmez que les valeurs (connexions) du tableau sont également dans la plage valide de 0 à n-1, en vous assurant qu'elles correspondent aux sommets existants

• Vérifiez les connexions en double ou les boucles automatiques car elles violent les conditions d'un graphique valide

• Vérifiez qu'il n'y a pas de connexions perdues, ce qui signifie que tous les sommets sont connectés pour former un graphe complet ou des composants connectés

Algorithmes DFS et BFS

• Depth First Search (DFS) est utilisé pour explorer les sommets et les arêtes d'un graphe en approfondissant le plus possible chaque branche avant de se retourner

pseudocode

procedure DFS(graph, start_vertex, visited)
   if start_vertex is not in visited:
      mark start_vertex as visited
      process start_vertex (e.g., check for cycles)
      for each neighbor in graph[start_vertex]:
      if neighbor is not in visited:
      DFS(graph, neighbor, visited)
   end if
end procedure
    pocedure DFS_Traversal(graph)
    visited = empty set
      for each vertex in graph:
      if vertex is not in visited:
         DFS(graph, vertex, visited)
   end for
end procedure

• La recherche en largeur d'abord (BFS) est un algorithme de parcours de graphe qui parcourt tous les sommets du graphe une couche à la fois. Cela en fait un excellent moyen de trouver des cycles dans les graphiques

pseudocode

procedure BFS(graph, start_vertex):
   create an empty queue Q
   create a set visited to keep track of visited vertices
   
   enqueue start_vertex into Q
   add start_vertex to visited set
   
   while Q is not empty:
      current_vertex = dequeue from Q
      for each neighbor_vertex of current_vertex:
         if neighbor_vertex is not in visited set:
            enqueue neighbor_vertex into Q
            add neighbor_vertex to visited set
      else:
         // A cycle is detected, return true
         return true
      // No cycle found, return false
      return false

Complexité

• Complexité temporelle

La complexité temporelle de BFS et DFS est O(V + E), où V est le nombre de sommets et E est le nombre d'arêtes.

• Complexité spatiale

La complexité temporelle de BFS et DFS est O(V).

Processus de détection de cycle étape par étape

Prenons un exemple avec un diagramme

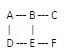
• Commencer à partir d'un ensemble vide pour surveiller les sommets visités

Visited set: {}

• Choisissez n'importe quel sommet comme point de départ du processus de détection de boucle. Nous sélectionnons le sommet A.

Visited set: {A}
Current Vertex: A

• Vérifiez les sommets adjacents du sommet actuel (A). Dans cet exemple, les voisins de A sont B et D. Ajoutez-les à l'ensemble d'accès et identifiez A comme son nœud parent

Visited set: {A, B, D}
Current Vertex: A
Parent of B: A
Parent of D: A

• B est le prochain sommet visité dans l'ensemble visité.

Visited set: {A, B, D}
Current Vertex: B
Parent of B: A

• Explorez les environs de B. Les voisins immédiats de B sont A, C et E. A est déjà dans l’ensemble de sommets visité, mais il n’est pas le parent de B et ne forme donc pas de cycle.

Visited set: {A, B, D, C, E}
Current Vertex: B

• Continuez jusqu'au prochain sommet visité, qui est D.

Visited set: {A, B, D, C, E}
Current Vertex: D
Parent of D: A

• J'ai trouvé la connaissance de D. A et E sont les plus proches voisins de D. Puisque A est déjà inclus dans l’ensemble d’accès et est le parent de D, il doit y avoir une arête (D -> A) reliant D à son parent. Cela indique que le graphique contient un cycle.

Cycle detected! There is an edge (D -> A) forming a cycle

Le processus se termine ici, nous avons réussi à détecter la boucle dans le graphique en utilisant BFS C'est (A->B->E->D->A).

Conclusion

En résumé, pour de nombreuses applications, il est important de pouvoir trouver des cycles dans un graphique construit à partir d'un tableau basé sur des paramètres donnés. Que vous utilisiez DFS ou BFS, ce processus permet de trouver des boucles possibles et de résoudre des problèmes réels impliquant des réseaux, des circuits et des relations. Une détection de boucle efficace peut augmenter la vitesse de votre algorithme et garantir l'exactitude de vos données.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!