Maison >interface Web >js tutoriel >Implémentation JavaScript de l'algorithme de recherche binaire
Implémentation JavaScript de l'algorithme de recherche binaire
- 王林original
- 2023-08-29 17:53:05736parcourir
Dans cet article, je comparerai les algorithmes de recherche linéaire et de recherche binaire. Vous apprendrez le pseudocode pour les algorithmes linéaires et binaires, consulterez des exemples illustrant les deux approches, comprendrez la complexité temporelle et obtiendrez un guide étape par étape sur la façon de mettre en œuvre les algorithmes.
Présentation
En tant que programmeur, vous souhaitez trouver la meilleure solution à un problème afin que votre code soit non seulement correct mais aussi efficace. Le choix d’un algorithme sous-optimal peut entraîner des délais d’exécution plus longs, une complexité de code accrue ou, pire encore, des plantages de programmes.
Vous avez peut-être utilisé des algorithmes de recherche pour localiser des éléments dans une collection de données. Le langage JavaScript dispose de plusieurs méthodes (telles que find) pour rechercher des éléments dans un tableau. Cependant, ces méthodes utilisent une recherche linéaire. L'algorithme de recherche linéaire commence au début de la liste et compare chaque élément à la valeur recherchée jusqu'à ce qu'il soit trouvé.
C'est bien lorsque le nombre d'éléments est petit. Cependant, lorsque vous recherchez de grandes listes contenant des milliers ou des millions d’éléments, vous avez besoin d’un meilleur moyen de localiser les éléments. C'est à ce moment-là que vous utilisez la recherche binaire.
Dans ce tutoriel, j'expliquerai comment fonctionne la recherche binaire et comment implémenter l'algorithme en JavaScript. Tout d’abord, passons en revue l’algorithme de recherche linéaire.
Recherche linéaire
Nous expliquerons d'abord comment implémenter la recherche linéaire en JavaScript. Nous allons en créer un appelé linearSearch 的函数,该函数接受整数或字符串和数组作为参数。该函数将在数组中的每个元素中搜索该值,如果找到,则返回该值在数组中的位置。如果数组中没有该值,则返回-1.
Pseudocode pour la recherche linéaire
Set found to false
Set position to −1
Set index to 0
while found is false and index < number of elements
if list[index] is equal to search value
Set found to true
Set position to index
else Add 1 to index
return position
Instructions étape par étape pour la recherche linéaire
Supposons que l'entrée de notre recherche linéaire soit [1,9,13,16,3,4,0,12]。如果我们要搜索的值是 16,则上述逻辑将返回 3。并且,如果我们搜索 11,上述逻辑将返回 -1. Décomposons-le.
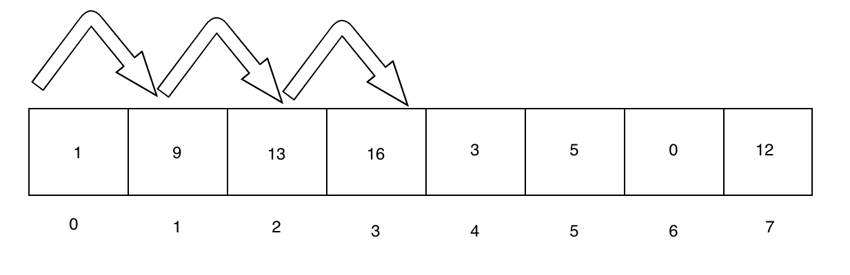
Nous initialisons l'algorithme en ajoutant found 设置为 false,将 position 设置为 -1,并将 index 设置为 0. Ensuite on itère :
| Étapes | index |
列表[索引] |
位置 |
找到 |
|---|---|---|---|---|
| 1 | 0 |
1 |
-1 |
false |
| 2 | 1 |
9 |
-1 |
false |
| 3 | 2 |
13 |
-1 |
false |
| 4 | 3 |
16 |
3 |
true |
如果我们对数组中不存在的元素遵循上述逻辑,您将看到代码返回 -1,因为 found = false,并且 position = -1 直到最后。 p>
线性搜索的Javascript实现
这是线性搜索算法的 JavaScript 实现:
function linearSearch(value, list) {
let found = false;
let position = -1;
let index = 0;
while(!found && index < list.length) {
if(list[index] == value) {
found = true;
position = index;
} else {
index += 1;
}
}
return position;
}
线性搜索的属性
需要注意的是,线性搜索算法不需要使用排序列表。此外,该算法可以定制以用于不同的场景,例如通过键搜索对象数组。如果您有一个包含名字和姓氏键的客户数据数组,您可以测试该数组是否包含具有指定名字的客户。在这种情况下,您不需要检查 list[index] 是否等于我们的搜索值,而是检查 list[index].first。
线性搜索的时间复杂度
如果搜索的元素是列表中的第一个元素,则可以实现最佳情况的时间复杂度。现在,搜索只需一次比较即可完成。因此,最好情况的时间复杂度为O(1)。
如果搜索的元素是最后一个元素或者不存在于列表中,则会出现最坏情况的时间复杂度。在这种情况下,搜索必须比较数组中的所有元素。我们说输入数据的长度为 n,这意味着由于进行了 n 次比较,总体时间复杂度为 O(n)。
在上面的示例中,我在包含八个元素的数组上使用了 linearSearch 函数。在最坏的情况下,当搜索值不在列表中或位于列表末尾时,该函数将必须进行八次比较。因为我们的数组很小,所以不需要使用不同的算法进行优化。然而,超过某一点,使用线性搜索算法就不再有效,这时使用二分搜索算法会更好。
线性搜索的平均时间复杂度也是O(n)。
线性搜索的空间复杂度
该算法的整体空间复杂度相当于数组的大小。因此,O(n)。您不需要保留任何额外的空间来完成此算法。
二分查找
假设您正在玩一个猜数字游戏。系统会要求您猜测 1 到 100 之间的一个数字。如果您的数字过高或过低,您将会得到提示。
您的策略是什么?你会随机选择数字吗?您会从 1 开始,然后是 2,依此类推,直到您猜对为止?即使您有无限的猜测,您也希望在尽可能少的尝试中做出正确的猜测。因此,您可以从猜测 50 开始。如果数字较大,您可以猜测 75。如果数字较小,则意味着数字在 50 到 75 之间,您会选择中间的数字。你会继续这样,直到得到正确的数字。这类似于二分搜索的工作原理。
有两种实现二分查找的方法:
- 迭代法
- 递归方法
迭代二分搜索的伪代码
下面是一些使用迭代方法表达二分搜索的伪代码:
do until the low and high pointers have not met or crossed
mid = (low + high)/2
if (x == arr[mid])
return mid
else if (x > arr[mid])
low = mid + 1
else
high = mid - 1
递归二分搜索的伪代码
这是使用递归方法实现二分查找的伪代码。
binarySearch(arr, x, low, high)
if low > high
return False
else
mid = (low + high) / 2
if x == arr[mid]
return mid
else if x > arr[mid]
return binarySearch(arr, x, mid + 1, high)
else
return binarySearch(arr, x, low, mid - 1)
无论使用何种技术,二分搜索算法始终使用分而治之的方法。
分步说明
让我们考虑一个数组 [1,9,13,16,3,5,0,12],其中 searchValue 是 13。
我们从执行二分搜索所需的排序数组开始。请注意,对数组进行排序的成本很高,但一旦完成,就可以多次有效地搜索该数组。
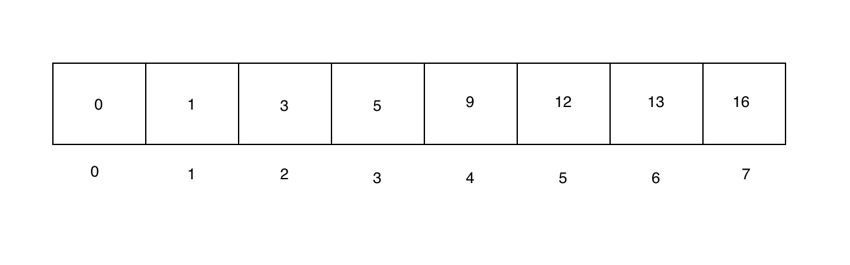
现在,高指针和低指针将分别设置为第一个和最后一个元素。中间指针设置为 (low - high) / 2 给出的索引。
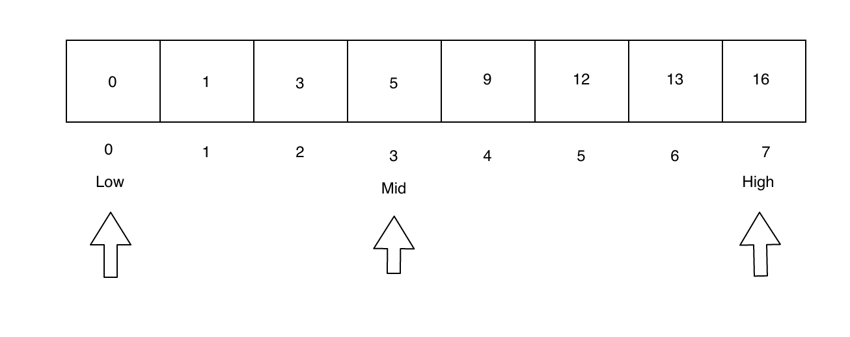
由于 searchValue > mid,我们需要搜索数组的右侧。因此,我们将 low 指针设置为紧接在 mid 之后,并将 mid 重置为位于 low 和 high 指针之间。
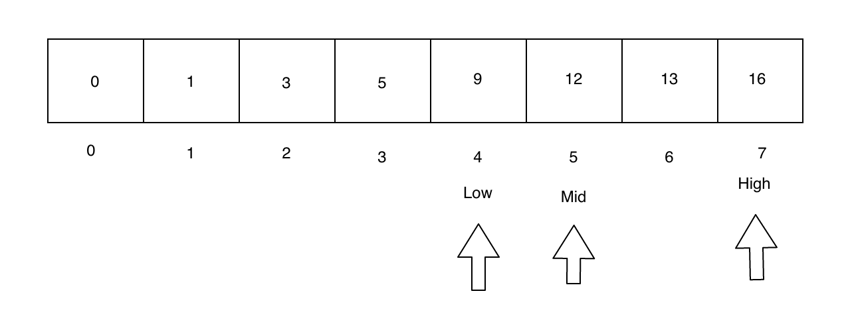
同样,目标值位于数组的右侧。我们再次调整低指针和高指针。现在低和中指针是相同的。
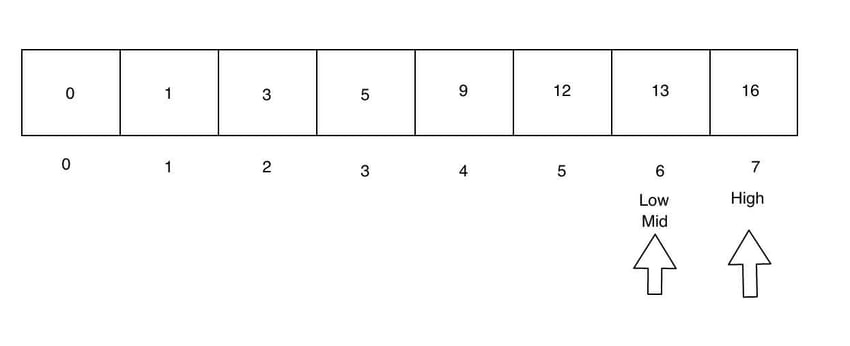
现在,在 mid 处找到了 searchValue,这意味着我们已经到达搜索的末尾!
| 步骤 | low |
mid |
high |
列表[mid] |
|---|---|---|---|---|
| 1 | 0 |
3 |
7 |
5 |
| 2 | 4 |
5 |
7 |
9 |
| 3 | 6 |
6 |
7 |
13 |
二分查找的Javascript实现
现在让我们用 JavaScript 编写二分搜索算法!
我们将创建一个函数 binarySearch,它接受一个值和一个数组作为参数。如果找到该值,它将返回列表中出现该值的索引。如果没有找到该值,则返回-1。这是我们用 JavaScript 编写的实现:
//note that list must be sorted for this function to work
function binarySearch(value, list) {
let low = 0; //left endpoint
let high = list.length - 1; //right endpoint
let position = -1;
let found = false;
let mid;
while (found === false && low <= high) {
mid = Math.floor((low + high)/2);
if (list[mid] == value) {
found = true;
position = mid;
} else if (list[mid] > value) { //if in lower half
high = mid - 1;
} else { //in in upper half
low = mid + 1;
}
}
return position;
}
时间复杂度
我们使用二分搜索来查找数组中的元素的主要原因之一是它的时间复杂度。在最佳情况下,二分查找的时间复杂度为O(1)。当数组中间的元素与搜索元素匹配时,就会发生这种情况。
在最坏的情况下,使用二分搜索搜索元素的时间复杂度为 O(log n) — 对于较大的 n 值,远低于 O(n)。要了解 log(n) 的增长速度比 n 慢多少,这里有一个 log(n) 典型值表.
| n | 日志(n) |
| 1 | 1 |
| 8 | 3 |
| 1024 | 10 |
| 1,000,000 | 19.9 |
| 1,000,000,000,000,000,000 | 59.8 |
因此,正如您所看到的,n 越大,二分搜索相对于线性搜索的改进就越大。
对于使用二分搜索来搜索项目,平均情况时间复杂度也是O(log n)。
空间复杂度
实现二分查找的空间复杂度还是O(n)。
二分查找的属性
与线性搜索不同,二分搜索使用排序列表。这让我们可以使用“分而治之”的算法来解决问题。
结论
在本教程中,我们了解了如何实现线性搜索和二分搜索算法。线性搜索算法更简单,并且不需要排序数组。然而,使用较大的数组效率很低。在最坏的情况下,算法必须搜索所有元素进行 n 次比较(其中 n 是元素数量)。
二分查找算法则需要先对数组进行排序,并且实现起来比较复杂。然而,即使考虑到排序成本,它的效率也更高。例如,具有 10 个元素的数组对于二分搜索最多进行 4 次比较,而对于线性搜索则最多进行 10 次比较,这并不是一个很大的改进。然而,对于具有 1,000,000 个元素的数组,二分查找的最坏情况也只有 20 次比较。这相对于线性搜索来说是一个巨大的改进!
了解如何使用二分搜索不仅仅是面试问题的练习。这是一项实用技能,可以让您的代码更高效地工作。
这篇文章已根据 Divya Dev 的贡献进行了更新。 Divya 是一位拥有五年以上经验的前端开发人员。她是安娜大学的毕业生和金牌获得者。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Une analyse approfondie du composant de groupe de liste Bootstrap
- Explication détaillée du currying de la fonction JavaScript
- Exemple complet de génération de mot de passe JS et de détection de force (avec téléchargement du code source de démonstration)
- Angularjs intègre l'interface utilisateur WeChat (weui)
- Comment basculer rapidement entre le chinois traditionnel et le chinois simplifié avec JavaScript et l'astuce permettant aux sites Web de prendre en charge le basculement entre les compétences en chinois simplifié et traditionnel_javascript

