Maison >développement back-end >Tutoriel Python >Analyse de régression et ligne droite la mieux ajustée à l'aide de Python
Analyse de régression et ligne droite la mieux ajustée à l'aide de Python
- 王林avant
- 2023-08-28 09:33:051680parcourir
Dans ce didacticiel, nous mettrons en œuvre l'analyse de régression et la ligne de meilleur ajustement à l'aide de la programmation Python
Présentation
L'analyse de régression est la forme la plus élémentaire d'analyse prédictive.
En statistique, la régression linéaire est une méthode de modélisation de la relation entre une valeur scalaire et une ou plusieurs variables explicatives.
En machine learning, la régression linéaire est un algorithme supervisé. Cet algorithme prédit une valeur cible basée sur des variables indépendantes.
Plus d'informations sur la régression linéaire et l'analyse de régression
En régression/analyse linéaire, la cible est une valeur réelle ou continue telle que le salaire, l'IMC, etc. Il est souvent utilisé pour prédire la relation entre une variable dépendante et un ensemble de variables indépendantes. Ces modèles s'adaptent généralement aux équations linéaires, mais il existe d'autres types de régression, notamment les polynômes d'ordre supérieur.
Avant d'ajuster un modèle linéaire aux données, il est nécessaire de vérifier s'il existe une relation linéaire entre les points de données. Cela ressort clairement de leur nuage de points. Le but de l’algorithme/modèle est de trouver la ligne la mieux adaptée.
Dans cet article, nous explorerons l'analyse de régression linéaire et sa mise en œuvre en C++.
L'équation de régression linéaire est de la forme Y = c + mx, où Y est la variable cible et X est la variable indépendante ou paramètre/variable explicatif. m est la pente de la droite de régression et c est l'origine. Puisqu'il s'agit d'une tâche de régression 2D, le modèle tente de trouver la ligne la mieux ajustée pendant l'entraînement. Il n’est pas nécessaire que tous les points soient alignés exactement sur la même ligne. Certains points de données peuvent se trouver sur la ligne et d’autres peuvent être dispersés sur la ligne. La distance verticale entre la ligne et les points de données est le résidu. La valeur peut être négative ou positive selon que le point se trouve en dessous ou au dessus de la ligne. Le résidu est une mesure de l’adéquation de la ligne aux données. L'algorithme est continu pour minimiser le résidu total.
Le résidu pour chaque observation est la différence entre la valeur prédite de y (la variable dépendante) et la valeur observée de y
$$mathrm{residual : =:actual:y:value:−:forecast:y:value}$$
$$mathrm{ri:=:yi:−:y'i}$$
La métrique la plus courante pour évaluer les performances d'un modèle de régression linéaire est appelée l'erreur quadratique moyenne, ou RMSE. L'idée de base est de mesurer dans quelle mesure les prédictions du modèle sont comparées aux observations réelles.
Donc, un RMSE élevé est « mauvais » et un RMSE faible est « bon »
L'erreur RMSE est
$$mathrm{RMSE:=:sqrt{frac{sum_i^n=1:(this:-:this')^2}{n}}}$$ p>
RMSE est la racine du carré moyen de tous les résidus.
Implémenté en utilisant Python
Exemple
# Import the libraries
import numpy as np
import math
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Generate random data with numpy, and plot it with matplotlib:
ranstate = np.random.RandomState(1)
x = 10 * ranstate.rand(100)
y = 2 * x - 5 + ranstate.randn(100)
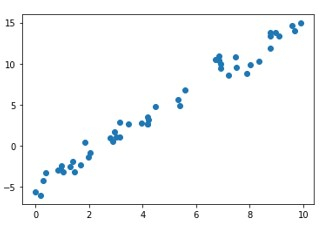
plt.scatter(x, y);
plt.show()
# Creating a linear regression model based on the positioning of the data and Intercepting, and predicting a Best Fit:
lr_model = LinearRegression(fit_intercept=True)
lr_model.fit(x[:70, np.newaxis], y[:70])
y_fit = lr_model.predict(x[70:, np.newaxis])
mse = mean_squared_error(y[70:], y_fit)
rmse = math.sqrt(mse)
print("Mean Square Error : ",mse)
print("Root Mean Square Error : ",rmse)
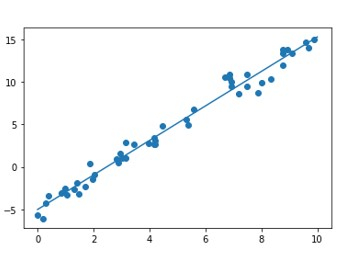
# Plot the estimated linear regression line using matplotlib:
plt.scatter(x, y)
plt.plot(x[70:], y_fit);
plt.show()
Sortie
Mean Square Error : 1.0859922470998231 Root Mean Square Error : 1.0421095178050257
Conclusion
L'analyse de régression est une technique très simple mais puissante utilisée pour l'analyse prédictive dans l'apprentissage automatique et les statistiques. L'idée réside dans sa simplicité et dans la relation linéaire sous-jacente entre les variables indépendantes et cibles.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

