Maison >développement back-end >C++ >Nombre de chemins de la racine aux feuilles avec au plus M nœuds consécutifs et valeur K
Nombre de chemins de la racine aux feuilles avec au plus M nœuds consécutifs et valeur K
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-08-25 22:45:131051parcourir
Présentation
L'arbre binaire est une structure de données fascinante avec un large éventail d'applications en informatique et en programmation. Un problème intéressant consiste à trouver le décompte d’un arbre donné composé d’un nœud parent et de ses enfants. Un arbre binaire est composé de nœuds, le nœud racine est déterminé et le nœud racine peut fournir des nœuds enfants en fonction des besoins de l'utilisateur. La valeur K est déterminée et la méthode de mouvement est sélectionnée par la valeur M.
Nombre de chemins racine à feuille
Le graphique est créé à l'aide de divers nœuds contenant des valeurs sous forme d'entiers. Cet article se concentre principalement sur le comptage depuis le nœud de départ ou le nœud racine jusqu'au nœud feuille ou au nœud enfant.
Exemple
Le graphique est créé à partir d'un arbre binaire avec différents nœuds.
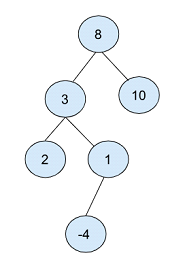
Dans l'arbre binaire ci-dessus, le nœud racine est sélectionné comme "8".
Créez ensuite deux nœuds, l'un avec une valeur de 3 et l'autre avec une valeur de 10, occupant les positions gauche et droite du nœud racine.
En prenant le nœud de valeur 2 comme racine, créez un autre nœud enfant avec les valeurs 2 et 1 comme nœuds gauche et droit respectivement.
Enfin, le nœud enfant de valeur 1 crée un nœud enfant de valeur -4.
Méthode 1 : code C++ pour calculer un chemin racine à feuille composé de jusqu'à M nœuds consécutifs avec K valeurs à l'aide d'une fonction récursive
Pour résoudre ce problème efficacement, nous utiliserons des concepts de base tels que l'algorithme de traversée d'arbre et la récursivité.
Algorithme
Étape 1 : Créez une structure pour représenter le nœud de l'arbre, qui comprend deux pointeurs (nœud enfant gauche et nœud enfant droit) et un champ entier pour stocker la valeur du nœud.
Étape 2 : Concevoir une fonction récursive pour parcourir l'arbre binaire en commençant par la racine, tout en suivant la longueur actuelle du chemin (initialisée à 0), le nombre d'occurrences consécutives (initialement définie à 0), la valeur cible K et le nombre maximum autorisé d'occurrences consécutives M .
Étape 3 : Appelez la fonction de manière récursive sur chaque sous-arbre gauche et droit, en transmettant des paramètres mis à jour tels que la longueur du chemin incrémentiel et le nombre d'occurrences consécutives (le cas échéant).
Étape 4 : Pour chaque nœud non vide visité lors du parcours :
a) Si sa valeur est égale à K, ajoutez un aux deux variables.
b) Remettez la variable à zéro si sa valeur ne correspond pas à K ou dépasse le nombre d'occurrences consécutives de M qui ont été rencontrées jusqu'à présent dans le chemin.
Étape 5 : Lors de la traversée de l'arbre, si la valeur d'un nœud enfant est nulle dans les cas gauche et droit, nous pouvons le gérer de deux manières, c'est-à-dire :
a) Vérifiez si la variable ne dépasse pas M.
b) Si oui, augmentez de 1 le nombre total de chemins qui satisfont à la condition.
Exemple
//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
int data;
struct Vertex* up;
struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
if (end == NULL || consCount > M) {
return 0;
}
//To check when the root is equal to the K value, increment by 1
if (end->data == K) {
currCount++;
consCount++;
} else {
//If it is not equal, it will return 0
currCount = 0;
}
if (end->up == NULL && end->down == NULL) {
if (currCount <= M) {
return 1;
} else {
return 0;
}
}
return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
Vertex* end = new Vertex();
end->data = 8;
end->up = new Vertex();
end->up->data = 3;
end->down = new Vertex();
end->down->data = 10;
end->up->up = new Vertex();
end->up->up->data = 2;
end->up->down = new Vertex();
end->up->down->data = 1;
end->up->down->up = new Vertex();
end->up->down->up->data = -4;
int K = 1; // Value of node
int M = 2; // Maximum consecutive nodes
int currCount = -1; // Current count
int consCount = -1; // Consecutive count
cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;
return 0;
}
Sortie
The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3
Conclusion
Dans cet article, nous explorons le problème du comptage du nombre de chemins depuis le sommet (c'est-à-dire la feuille) jusqu'à la pointe ou la racine. De tels problèmes peuvent être résolus efficacement en utilisant des algorithmes de traversée d’arbres et des techniques récursives en C++. Le processus de parcours d’un arbre binaire peut sembler difficile, mais cela devient facile avec des exemples.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

