Maison >Java >javaDidacticiel >Programmation dynamique de mémisation (1D, 2D et 3D) en Java
Programmation dynamique de mémisation (1D, 2D et 3D) en Java
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-08-23 14:13:491468parcourir
La mémoisation est une technique basée sur la programmation dynamique utilisée pour améliorer les performances des algorithmes récursifs en garantissant qu'une méthode ne s'exécute pas plusieurs fois sur le même ensemble d'entrées, en enregistrant les résultats (stockés dans un tableau) des entrées fournies. La mémorisation peut être réalisée grâce à une approche descendante qui met en œuvre des méthodes récursives.
Comprenons cette situation à travers un exemple de base de séquence de Fibonacci.
Mémoisation 1-D
Nous considérerons un algorithme récursif avec un seul paramètre non constant (une seule valeur d'un paramètre change), cette méthode est donc appelée mémoisation 1-D. Le code suivant permet de trouver le Nième (tous les termes jusqu'à N) dans la séquence de Fibonacci.
Exemple
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}Output
Si nous exécutons le code ci-dessus avec n=5, la sortie suivante sera générée. La valeur de Fibonacci pour
Calculating fibonacci number for: 5 Calculating fibonacci number for: 4 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2 Calculating fibonacci number for: 2 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2
n=5 est : 5
Notez que les nombres de Fibonacci pour 2 et 3 sont calculés plusieurs fois. Comprenons mieux en dessinant l'arbre de récursion ci-dessus pour la condition n=5.
Les deux enfants d'un nœud représenteront les appels récursifs qu'il effectue. Vous pouvez voir que F(3) et F(2) sont calculés plusieurs fois, ce qui peut être évité en mettant en cache les résultats après chaque étape.
Nous utiliserons une variable d'instance memoize Set pour mettre en cache les résultats. Vérifiez d'abord si n existe déjà dans l'ensemble memoize, si c'est le cas, renvoyez la valeur sinon, calculez la valeur et ajoutez-la à l'ensemble.
Exemple
import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
public int fibMemoize(int input) {
if (input == 0)
return 0;
if (input == 1)
return 1;
if (this.memoizeSet.containsKey(input)) {
System.out.println("Getting value from computed result for " + input);
return this.memoizeSet.get(input);
}
int result = fibMemoize(input - 1) + fibMemoize(input - 2);
System.out.println("Putting result in cache for " + input);
this.memoizeSet.put(input, result);
return result;
}
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}
public static void main(String[] args) {
TutorialPoint tutorialPoint = new TutorialPoint();
System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
}
}Output
Si nous exécutons le code ci-dessus, la sortie suivante sera générée
Adding result in memoizeSet for 2 Adding result in memoizeSet for 3 Getting value from computed result for 2 Adding result in memoizeSet for 4 Getting value from computed result for 3 Adding result in memoizeSet for 5
La valeur de Fibonacci pour n=5 est : 5
Comme vous pouvez le voir ci-dessus, les valeurs de Fibonacci pour 2 et 3 Le numéro d'acte ne sera pas recalculé. Ici, nous introduisons un HashMap mémorise pour stocker les valeurs calculées. Avant chaque calcul de Fibonacci, vérifiez si la valeur de l'entrée a été calculée dans la collection. Sinon, ajoutez la valeur de l'entrée spécifique au milieu de la collection.
Mémorisation 2-D
Dans le programme ci-dessus, nous n'avons qu'un seul paramètre non constant. Dans le programme suivant, nous prendrons un exemple de programme récursif qui a deux paramètres qui changent de valeur après chaque appel récursif, et nous implémenterons la mémorisation sur les deux paramètres non constants pour l'optimisation. C'est ce qu'on appelle la mémorisation 2D.
Par exemple : nous implémenterons la sous-séquence commune la plus longue standard (LCS). Si un ensemble de séquences est donné, le problème de la sous-séquence commune la plus longue est de trouver la sous-séquence commune à toutes les séquences qui a la plus grande longueur. Il y aura 2^n combinaisons possibles.
Exemple
class TP {
static int computeMax(int a, int b) {
return (a > b) ? a : b;
}
static int longestComSs(String X, String Y, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (X.charAt(m - 1) == Y.charAt(n - 1))
return 1 + longestComSs(X, Y, m - 1, n - 1);
else
return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
}
public static void main(String[] args) {
String word_1 = "AGGTAB";
String word_2 = "GXTXAYB";
System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
}
}Sortie
Si nous exécutons le code ci-dessus, la sortie suivante sera générée
Length of LCS is 4
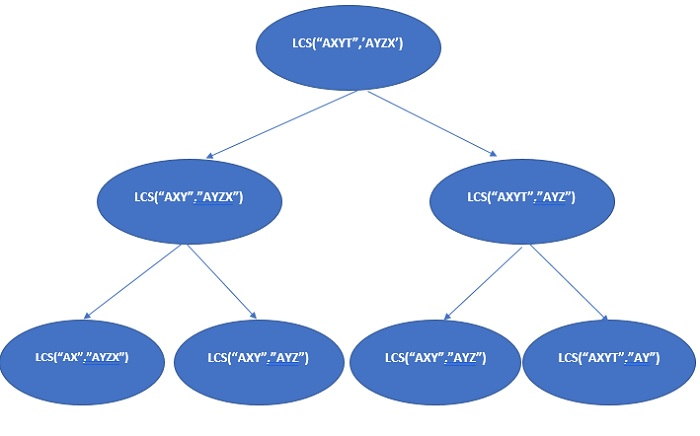
Dans l'arbre de récursion ci-dessus, lcs("AXY", "AYZ") est résolu plusieurs fois.
En raison de la nature de ce problème avec des sous-structures qui se chevauchent, les calculs répétés des mêmes sous-problèmes peuvent être évités en utilisant la mémorisation ou la tabulation.
La méthode de mémorisation du code récursif est implémentée comme suit.
Exemple
import java.io.*;
import java.lang.*;
class testClass {
final static int maxSize = 1000;
public static int arr[][] = new int[maxSize][maxSize];
public static int calculatelcs(String str_1, String str_2, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (arr[m - 1][n - 1] != -1)
return arr[m - 1][n - 1];
if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
return arr[m - 1][n - 1];
}
else {
int a = calculatelcs(str_1, str_2, m, n - 1);
int b = calculatelcs(str_1, str_2, m - 1, n);
int max = (a > b) ? a : b;
arr[m - 1][n - 1] = max;
return arr[m - 1][n - 1];
}
}
public static void main(String[] args) {
for (int i = 0; i < 1000; i++) {
for (int j = 0; j < 1000; j++) {
arr[i][j] = -1;
}
}
String str_1 = "AGGTAB";
String str_2 = "GXTXAYB";
System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
}
}Output
Si nous exécutons le code ci-dessus, la sortie suivante sera générée
Length of LCS is 4
Method
Observé qu'il y a 4 paramètres dans la méthode (calculatelcs), dont il y a 2 constantes (ne affectent la mémorisation) , et il y a 2 paramètres non constants (m et n), dont les valeurs changeront à chaque fois que la méthode est appelée de manière récursive. Afin de réaliser la mémorisation, nous introduisons un tableau bidimensionnel pour stocker la valeur calculée de lcs(m,n), qui est stockée dans arr[m-1][n-1]. Lors de l'appel à nouveau de la fonction avec les mêmes paramètres m et n, nous n'effectuons plus d'appel récursif, mais renvoyons directement arr[m-1][n-1], car le lcs(m, n) précédemment calculé a été stocké dans arr [m-1][n-1], réduisant ainsi le nombre d'appels récursifs.
Mémoisation tridimensionnelle
Il s'agit d'une méthode de mémorisation pour les programmes récursifs avec 3 paramètres non constants. Ici, nous prenons comme exemple le calcul de la longueur LCS de trois chaînes.
L'approche ici consiste à générer toutes les sous-séquences possibles d'une chaîne donnée (il y a 3ⁿ sous-séquences possibles au total) et à faire correspondre la sous-séquence commune la plus longue parmi elles.
Nous présenterons un tableau tridimensionnel pour stocker les valeurs calculées. Considérez les sous-séquences.
A1[1...i] je
A2[1...j] j
Si nous trouvons un caractère commun (X[i]==Y[j]==Z[k]), nous devons traiter de manière récursive les caractères restants. Sinon, nous calculerons le maximum des cas suivants - Gardez
- f(N,M,K)={1+f(N -1,M-1,K-1)si (X[N] ==Y[M]==Z[K]maximum(f(N-1,M,K),f(N,M-1, K),f(N,M,K-1))}
- f(N-1,M,K) = Réserver X[i] pour traiter récursivement d'autres caractères
- f(N,M- 1,K) = Réserver Y[j] pour traiter d'autres caractères de manière récursive
import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
public static int[][][] arr = new int[100][100][100];
static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
arr[i][j][0] = 0;
}
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= o; j++) {
arr[0][i][j] = 0;
}
}
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= o; j++) {
arr[i][0][j] = 0;
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= o; k++) {
if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
}
else {
arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
}
}
}
}
return arr[m][n][o];
}
static int calculateMax(int a, int b, int c) {
if (a > b && a > c)
return a;
if (b > c)
return b;
return c;
}
public static void main(String[] args) {
String str_1 = "clued";
String str_2 = "clueless";
String str_3 = "xcxclueing";
int m = str_1.length();
int n = str_2.length();
int o = str_3.length();
System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
}
}Si nous exécutons le code ci-dessus, la sortie suivante sera générée
Length of LCS is 4
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

