Utilisez-le tous les jours ! Savez-vous ce qu'est le HASH ?

Avez-vous déjà utilisé HashMap ? Alors, avez-vous sérieusement compris ce qu'est le Hash ? Cet article vous guidera à travers une étude approfondie de l'algorithme de hachage à un niveau de principe.

1. Le concept de hachage

L'idée principale de la méthode de hachage est de déterminer l'adresse de stockage en fonction de la valeur du code clé du nœud : en prenant la valeur du code clé K comme variable indépendante, via une certaine relation fonctionnelle h(K ) (appelée fonction de hachage), calculer la valeur de fonction correspondante, interpréter cette valeur comme l'adresse de stockage du nœud et stocker le nœud dans cette unité de stockage. Lors de la récupération, utilisez la même méthode pour calculer l'adresse, puis rendez-vous dans l'unité correspondante pour obtenir le nœud que vous recherchez. Les nœuds peuvent être rapidement récupérés grâce au hachage. Le hachage (également appelé « hachage ») est une méthode de stockage importante et une méthode de récupération courante.

La structure de stockage construite selon la méthode de stockage de hachage est appelée table de hachage. Une position dans la table de hachage est appelée un emplacement. Le cœur de la technologie de hachage est la fonction de hachage. Pour toute table de recherche dynamique DL donnée, si une fonction de hachage « idéale » h et la table de hachage HT correspondante sont sélectionnées, alors pour chaque élément de données X dans DL. La valeur de fonction h (X.key) est l'emplacement de stockage de X dans la table de hachage HT. L'élément de données X sera placé à cette position lors de l'insertion (ou de la création d'un tableau), et sera également recherché à cette position lors de la récupération de X. L'emplacement de stockage déterminé par la fonction de hachage est appelé adresse de hachage. Par conséquent, le cœur du hachage est le suivant : la fonction de hachage détermine la relation correspondante entre la valeur du code clé (X.key) et l'adresse de hachage h (X.key). Grâce à cette relation, le stockage et la récupération organisationnels sont réalisés.

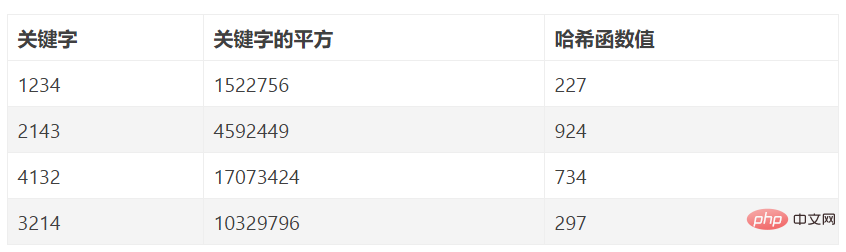
Généralement, l'espace de stockage de la table de hachage est un tableau unidimensionnel HT[M], et l'adresse de hachage est l'indice du tableau. Le but de la conception d'une méthode de hachage est de concevoir une certaine fonction de hachage h, 0<=h(K)

2. Fonction de hachage

Dans la discussion suivante, nous supposons que nous avons affaire à des codes clés dont les valeurs sont des entiers, sinon nous pouvons toujours établir une correspondance biunivoque entre les codes clés et les entiers positifs, de sorte que Convertir la récupération de la clé en une récupération de l'entier positif correspondant en même temps, on suppose en outre que la valeur de la fonction de hachage est comprise entre 0 et M-1. Les principes de sélection d'une fonction de hachage sont les suivants : l'opération est aussi simple que possible ; la plage de valeurs de la fonction doit être dans la portée de la table de hachage ; les nœuds doivent être répartis uniformément autant que possible, c'est-à-dire essayer de faire différentes clés ont des valeurs de fonction de hachage différentes. Divers facteurs doivent être pris en compte : longueur de clé, taille de la table de hachage, distribution des clés, fréquence de récupération des enregistrements, etc. Ci-dessous, nous présentons plusieurs fonctions de hachage couramment utilisées.

1. Méthode de division du reste

Comme son nom l'indique, la méthode du reste consiste à diviser le code clé x par M (en prenant souvent la longueur de la table de hachage) et à prendre le reste comme adresse de hachage. La méthode du reste est presque la méthode de hachage la plus simple, et la fonction de hachage est : h(x) = x mod M.

2. Méthode d'arrondi du reste de multiplication

Lorsque vous utilisez cette méthode, multipliez d'abord le code clé par une constante A (0< A < 1) et extrayez la partie décimale du produit. Ensuite, multipliez cette valeur par l'entier n, arrondissez le résultat et utilisez-le comme adresse de hachage. La fonction de hachage est : hash (key) = _LOW(n × (A × key % 1)). Parmi eux, "A × key % 1" signifie prendre la partie décimale de A × key, c'est-à-dire : A × key % 1 = A × key - _LOW(A × key), et _LOW(X) signifie prendre la partie entière de X

3. Méthode carrée

Étant donné que la division entière s'exécute généralement plus lentement que la multiplication, éviter consciemment l'utilisation de l'opération de reste peut améliorer le temps d'exécution de l'algorithme de hachage. La mise en œuvre spécifique de la méthode du milieu carré consiste à trouver d'abord la valeur carrée du code clé pour augmenter la différence entre des nombres similaires, puis à prendre les chiffres du milieu (souvent des bits binaires) en fonction de la longueur du tableau comme fonction de hachage. valeur. Étant donné que les chiffres du milieu d'un produit sont liés à chaque chiffre du multiplicateur, l'adresse de hachage résultante est plus uniforme.

4. Méthode d'analyse numérique

Supposons que chaque mot-clé de l'ensemble de mots-clés est composé de s chiffres (u1, u2, …, us), analysez l'ensemble de mots-clés et extrayez-en plusieurs uniformément répartis. bits ou leur combinaison comme adresses. La méthode d'analyse numérique est une méthode consistant à prendre certains bits numériques avec des valeurs relativement uniformes dans les mots-clés des éléments de données comme adresse de hachage. Autrement dit, lorsque le mot-clé comporte de nombreux chiffres, vous pouvez analyser les bits du mot-clé et supprimer les bits inégalement répartis en tant que valeur de hachage. Cela ne convient que lorsque toutes les valeurs des mots-clés sont connues. En analysant la distribution, la plage de valeurs du mot clé est convertie en une plage de valeurs de mot clé plus petite.

Par exemple : Pour construire une table de hachage avec le nombre d'éléments de données n=80 et la longueur de hachage m=100. Sans perte de généralité, nous ne donnons ici que 8 mots-clés pour analyse. Les 8 mots-clés sont les suivants :

K1=61317602 K2=61326875 K3=62739628 K4=61343634

K5=62706815 K6=62774638 K7= 61381262 K8. =61394220

L'analyse des 8 mots-clés ci-dessus montre que les valeurs​​des 1er, 2ème, 3ème et 6ème chiffres de gauche à droite du mot-clé sont relativement concentrées et ne conviennent pas comme adresses de hachage. 7ème, les valeurs de 8 bits sont relativement égales et deux d'entre elles peuvent être sélectionnées comme adresse de hachage. Supposons que les deux derniers chiffres soient sélectionnés comme adresse de hachage, alors les adresses de hachage de ces huit mots-clés sont : 2, 75, 28, 34, 15, 38, 62, 20.

Cette méthode convient pour : pouvoir estimer à l'avance la fréquence d'apparition de différents nombres dans chaque chiffre de tous les mots-clés.

5. Méthode de conversion de base

Traitez la valeur clé comme un nombre dans une autre base, puis convertissez-la en numéro d'origine, puis sélectionnez-en quelques-unes comme adresse de hachage.

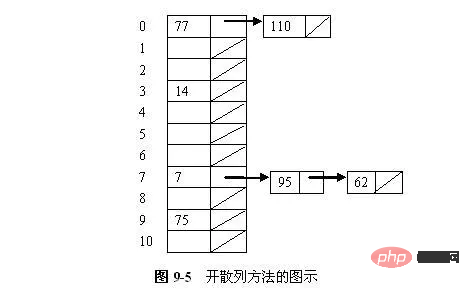
Exemple Hash(80127429)=(80127429)13=8137+0136+1135+2134+7133+4132+2*131+9=(502432641)10 Si vous prenez les trois chiffres du milieu comme valeur de hachage, vous obtenez Hash (80127429) =432 Afin d'obtenir une bonne fonction de hachage, plusieurs méthodes peuvent être utilisées en combinaison, comme changer d'abord la base, puis plier ou équarrir, etc. Tant que le hachage est uniforme, vous pouvez le reconstituer à volonté.

6. Méthode de pliage

Parfois, le code clé contient de nombreux chiffres, et il est trop compliqué d'utiliser la méthode du carré pour calculer, alors le code clé peut être divisé en plusieurs parties avec le même nombre de chiffres ( le nombre de chiffres dans la dernière partie peut être différent), puis prenez la somme de superposition de ces parties (en supprimant le report) comme adresse de hachage. Cette méthode est appelée méthode de pliage.

est divisé en :

• Superposition Shift : Alignez et ajoutez les bits bas des parties divisées.
• Superposition de bordure : pliez d'avant en arrière à partir d'une extrémité le long de la limite de séparation, puis alignez et ajoutez.

3. Stratégies de résolution des conflits

Bien que le but de la fonction de hachage soit de minimiser les conflits, en fait les conflits sont inévitables. Par conséquent, nous devons examiner des stratégies de résolution des conflits. Les techniques de résolution de conflits peuvent être divisées en deux catégories : le hachage ouvert (également appelé fermeture éclair, chaînage séparé) et le hachage fermé (hachage fermé, également appelé adressage ouvert). La différence entre ces deux méthodes est que la méthode de hachage ouverte stocke la clé en collision en dehors de la table de hachage principale, tandis que la méthode de hachage fermée stocke la clé en collision dans un autre emplacement de la table.

1. Méthode de liste chaînée séparée

(1) Méthode Zipper

Une forme simple de la méthode de hachage consiste à définir chaque emplacement de la table de hachage comme tête d'une liste chaînée. Tous les enregistrements hachés vers un emplacement spécifique sont placés dans la liste chaînée de cet emplacement. La figure 9-5 illustre une table de hachage ouverte dans laquelle chaque emplacement stocke un enregistrement et un pointeur vers le reste de la liste chaînée. Ces 7 nombres sont stockés dans une table de hachage à 11 emplacements, et la fonction de hachage utilisée est h(K) = K mod 11. L'ordre d'insertion des nombres est 77, 7, 110, 95, 14, 75 et 62. Il y a 2 valeurs hachées vers l'emplacement 0, 1 valeur hachée vers l'emplacement 3, 3 valeurs hachées vers l'emplacement 7 et 1 valeur hachée vers l'emplacement 9.

2. Méthode de hachage fermée (méthode d'adresse ouverte)

La méthode de hachage fermée stocke tous les enregistrements directement dans la table de hachage. Chaque clé de clé d'enregistrement a une position de base calculée par une fonction de hachage, c'est-à-dire h(key). Si une clé doit être insérée et qu'un autre enregistrement occupe déjà la position de base de R (une collision se produit), alors R est stocké à une autre adresse dans la table et la politique de résolution de conflit détermine de quelle adresse il s'agit.

L'idée de base de la résolution des conflits avec une table de hachage fermée est la suivante : lorsqu'un conflit se produit, utilisez une certaine méthode pour générer une séquence d'adresses de hachage d0, d1, d2,...di,...dm-1 pour le code clé K. Parmi eux, d0=h (K) est appelé la position d'origine de l'adresse de base de K ; tous les di (0< i< m) sont des adresses de hachage ultérieures. Lorsque K est inséré, si le nœud à l'adresse de base est déjà occupé par d'autres éléments de données, il sera sondé séquentiellement selon la séquence d'adresses ci-dessus, et la première position libre ouverte di trouvée sera utilisée comme emplacement de stockage de K ; si tous les hachages suivants Aucune adresse n'est libre, ce qui indique que la table de hachage fermée est pleine et qu'un débordement est signalé. De manière correspondante, lors de la récupération de K, la séquence d'adresses suivantes avec la même valeur sera recherchée séquentiellement, et la position di sera renvoyée lorsque la récupération sera réussie ; si une adresse libre ouverte est rencontrée lors de la récupération le long de la séquence de sondage, cela signifie que ; il n'y a pas de clé à rechercher dans le code de la table. Lors de la suppression de K, nous recherchons également séquentiellement en fonction de la séquence d'adresses successeurs avec la même valeur. Si nous constatons qu'une certaine position di a la valeur K, nous supprimons l'élément de données à cette position di (l'opération de suppression marque en fait simplement le. nœud à supprimer); Si une adresse libre ouverte est rencontrée, cela signifie qu'il n'y a pas de clé à supprimer dans la table. Par conséquent, pour les tables de hachage fermées, la méthode de construction d’une séquence d’adresses de hachage ultérieures est la méthode de gestion des conflits.

Différentes méthodes de formation d'enquêtes conduisent à différentes méthodes de résolution des conflits. Vous trouverez ci-dessous plusieurs méthodes de construction courantes.

(1) Méthode de détection linéaire

considère la table de hachage comme une table en anneau. Si un conflit se produit à l'adresse de base d (c'est-à-dire h(K)=d), les unités d'adresse suivantes sont sondées en séquence : d +1 , d+2,...,M-1,0,1,...,d-1 jusqu'à ce qu'une adresse libre soit trouvée ou qu'un nœud avec le code clé soit trouvé. Bien entendu, si vous revenez à l'adresse d après avoir recherché le long de la séquence de sondage, cela signifie un échec, que vous effectuiez une opération d'insertion ou une opération de récupération. La fonction de sonde pour une sonde linéaire simple est : p(K,i) = i

Exemple 9.7 On sait qu'un ensemble de codes clés est (26, 36, 41, 38, 44, 15, 68, 12, 06, 51, 25), la longueur de la table de hachage M = 15, utilisez le linéaire méthode d'exploration pour résoudre les conflits et construire cet ensemble de tables de hachage de clés. Parce que n=11, utilisez la méthode du reste pour construire une fonction de hachage et sélectionnez le plus grand nombre premier P=13 inférieur à M. La fonction de hachage est alors : h(key) = key%13. Insérez chaque nœud dans l'ordre : 26 : h(26) = 0, 36 : h(36) = 10, 41 : h(41) = 2, 38 : h(38) = 12, 44 : h(44) = 5 . Lorsque 15 est inséré, son adresse de hachage est 2. Puisque 2 est déjà occupé par l'élément avec le code clé 41, il doit être sondé. Selon la méthode de sondage séquentiel, il est évident que 3 est une adresse libre ouverte, elle peut donc être placée dans l'unité 3. De même, 68 et 12 peuvent être placés respectivement dans les unités 4 et 13

(2) Méthode de sondage quadratique

L'idée de base de la méthode de sondage quadratique est la suivante : les adresses de hachage suivantes générées ne sont pas continues, mais sautées. pour laisser de la place aux éléments de données ultérieurs afin de réduire l’agrégation. La séquence de détection de la méthode de détection secondaire est : 12, -12, 22, -22,... etc. C'est-à-dire que lorsqu'un conflit survient, les synonymes sont hachés d'avant en arrière aux deux extrémités de la première adresse. La formule pour trouver la prochaine adresse ouverte est la suivante :

(3) Méthode de sondage aléatoire

La fonction de sondage idéale doit sélectionner au hasard la position suivante à partir d'un emplacement non visité dans la séquence de sondage, c'est-à-dire que la séquence de sonde doit être une permutation aléatoire des positions de la table de hachage. Cependant, nous ne pouvons pas réellement sélectionner au hasard une position dans la séquence de sonde car la même séquence de sonde ne peut pas être établie lors de la récupération de la clé. Cependant, nous pouvons faire quelque chose comme un sondage pseudo-aléatoire. Dans le sondage pseudo-aléatoire, le i-ème emplacement de la séquence de sondage est (h(K) + ri) mod M, où ri est une séquence "aléatoire" de nombres compris entre 1 et M - 1. Toutes les insertions et récupérations utilisent le même numéro « aléatoire ». La fonction de sonde sera p(K,i) = perm[i - 1], où perm est un tableau de longueur M - 1 contenant une séquence aléatoire de valeurs de 1 à M - 1.

Exemple :

Par exemple, la longueur de table de hachage connue m=11, la fonction de hachage est : H (clé) = clé % 11, puis H (47) = 3, H (26) = 4, H (60 )=5, en supposant que le mot-clé suivant est 69, alors H(69)=3, ce qui est en conflit avec 47. Si la détection linéaire puis le hachage sont utilisés pour gérer les conflits, l'adresse de hachage suivante est H1=(3 + 1)% 11 = 4. S'il y a toujours un conflit, l'adresse de hachage suivante est H2=(3 + 2)% 11 = 5. , il y a toujours un conflit, continuez à trouver l'adresse de hachage suivante comme H3 = (3 + 3)% 11 = 6, il n'y a plus de conflit à ce moment, remplissez 69 dans l'unité 5, voir Figure 8.26 (a ). Si vous utilisez la détection secondaire et le hachage pour gérer les conflits, l'adresse de hachage suivante est H1 = (3 + 12)% 11 = 4. Si le conflit persiste, recherchez l'adresse de hachage suivante H2 = (3 - 12)% 11 = 2. Il n'y a pas de conflit pour le moment. Remplissez 69 dans l'unité 2, voir Figure 8.26 (b). Si la détection pseudo-aléatoire puis le hachage sont utilisés pour gérer les conflits et que la séquence de nombres pseudo-aléatoires est : 2, 5, 9,…….., alors l'adresse de hachage suivante est H1 = (3 + 2)% 11 = 5, et il y a toujours un conflit, puis trouvez l'adresse de hachage suivante comme H2 = (3 + 5)% 11 = 8. Il n'y a plus de conflit à ce moment-là. Remplissez 69 dans l'unité 8, voir Figure 8.26 (c).

(4)Méthode de détection de double hachage

Le sondage pseudo-aléatoire et le sondage secondaire peuvent éliminer le problème de l'agrégation de base, c'est-à-dire que les codes clés avec des adresses de base différentes et que certains segments de leurs séquences de sondage se chevauchent. Cependant, si deux clés sont hachées vers la même adresse de base, la même séquence de sonde sera toujours obtenue en utilisant les deux méthodes et l'agrégation se produira toujours. En effet, la séquence de sondage générée par le sondage pseudo-aléatoire et le sondage secondaire est uniquement fonction de l'adresse de base, et non de la valeur de clé d'origine. Ce problème est appelé clustering secondaire.

Afin d'éviter une agrégation secondaire, nous devons faire de la séquence de sonde une fonction de la valeur de la clé d'origine plutôt qu'une fonction de la position de base. La méthode de détection de double hachage utilise la deuxième fonction de hachage comme constante, saute le terme constant à chaque fois et effectue une détection linéaire.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!