Un article pour vous aider à comprendre les fonctions récursives de Python

1. Qu'est-ce qu'une fonction récursive ?

Au sein d'une fonction, vous pouvez appeler d'autres fonctions. Une fonction est récursive si elle s'appelle en interne.

2. Principe d'appel récursif de fonctions

• En fait, les fonctions récursives sont exécutées de manière récursive sur la mémoire de la pile, et chaque exécution récursive consomme de la mémoire de la pile.

• La taille de la mémoire de la pile est un facteur important pour limiter la profondeur de la récursion

3. Analyse de cas

1. Trouver la factorielle

Calculez factorielle n = 1 x 2 x 3 x … x n,

peut être représenté par la fonction fact(n).

fact(n) = n! = 1 x 2 x 3 x … x (n-1) x n = (n-1)! x n = fact(n-1) x n

fact(n)可以表示为n x fact(n-1)，只有n=1时需要特殊处理。

Donc, fact(n) s'écrit récursivement :

def fact(n):    if n == 1:        return 1    return n * fact(n - 1)

如果计算fact(6)，可以根据函数定义看到计算过程如下：

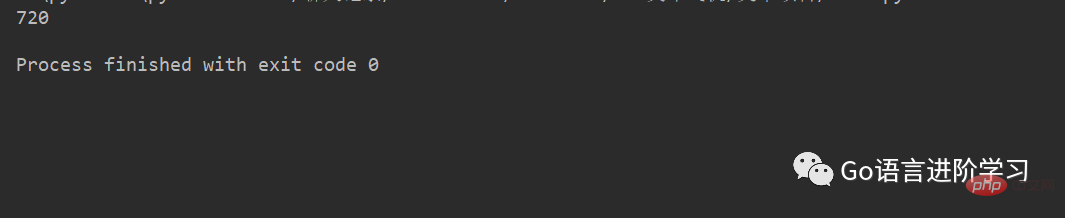
def fac(n):    if n==1:        return 1    else:        res=n*fac(n-1)        return  res
print(fac(6))

运行结果：

2. 斐波拉契级数

有这样一个数列：1，1，2，3，5，8，13，21，34…。其第一元素和第二个元素等于 1，其他元素等于其前面两个元素的和。

例：

def fab(n):  # 定义斐波拉契级数    if n in [1, 2]:  # 如果n=1或者2      return 1    return fab(n - 1) + fab(n - 2)  # n>2

print(fab(1))  # 斐波拉契级数的第一个元素
print(fab(2))  # 斐波拉契级数的第二个元素
print(fab(8))  # 斐波拉契级数的第8个元素print(fab(13))  # 斐波拉契级数的第9个元素

运行结果：

3. 递归函数的优点

定义简单，逻辑清晰。理论上，所有的递归函数都可以写成循环的方式，但循环的逻辑不如递归清晰。

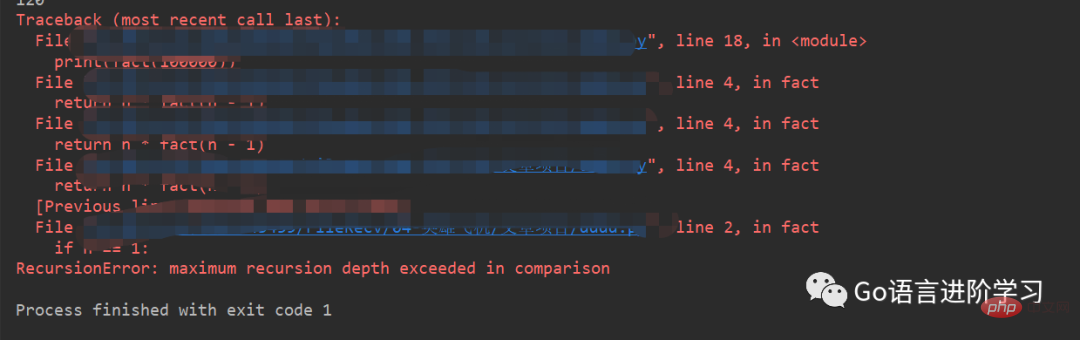
递归需要注意递归的深度。由于递归会产生多次函数调用，而函数调用会消耗代码的栈空间，如果递归的深度太大，会导致栈溢出。以上面的阶乘为例，如果计算 100000 的阶乘，在一般机器上都会出现栈溢出的问题。

print(fac(10000))

如下所示：

4. Résumé

Cet article est basé sur les bases de Python. L'interpréteur standard de Python n'est pas optimisé pour la récursion de queue, et toute fonction récursive aura un débordement de pile. Cet article présente les avantages et les inconvénients de l'utilisation de fonctions récursives. L'avantage est que la logique est simple et claire, mais l'inconvénient est que des appels excessifs peuvent provoquer un débordement de pile.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!